図形の性質｜角の二等分線と比について
今回から新しい単元になります。数Ａの「図形の性質」という単元です。
数学１・Ａ全般に言えることですが、この単元も中学での履修内容がベースになっています。もちろん、新しい定理や公式が出てくるのですが、その導出ではこれまでに学習した図形の性質を利用します。
復習もかねて導出の過程をしっかり熟読しましょう。その際には、中学の教科書も参照しながら学習すると良いでしょう。
なお、記事の画像が見辛いときはクリックすると拡大できます。
角の二等分線と比
角の二等分線と比の関係については、既に中学で学習しています。三角形の面積比を求めるときに利用しました。
三角形の面積比に利用できる理由を知らないままに覚えたかもしれませんが、その理由をこの単元で理解しましょう。
また、角の二等分線と比の関係だけでなく、この単元では内分や外分などの新しい用語についても学習します。これらとのつながりもしっかりと理解しましょう。
ここで学習する用語は以下のようなものがあります。
単元「角の二等分線と比」で学習する用語
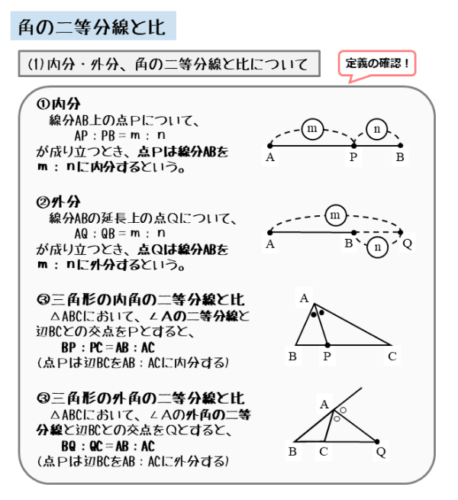
- 内分
- 外分
- 三角形の内角の二等分線と比
- 三角形の外角の二等分線と比
線分の内分
内分とは、線分上の点で線分を分けることです。
一般に「線分ＡＢについて、ＡＰ：ＢＰ＝ｍ：ｎが成り立つとき、線分ＡＢは点Ｐによってｍ：ｎに内分される」と言います。
また、線分を内分する点を内分点と言います。内分点は図を見ると分かるように必ず線分上に存在します。
内分後の線分の長さ
線分は、内分されるといくつかの線分に分割されます。分割された各線分の長さは、内分比を利用して表されます。
内分後の線分の長さを求める問題は頻出なので、確実にマスターしよう。
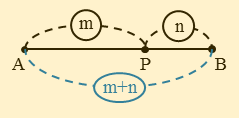
たとえば、線分ＡＢを２：１に内分する点をＰとします。このとき、線分ＡＰ，ＢＰの長さを線分ＡＢで表わしてみましょう。
線分ＡＢを内分点Ｐによって２：１に内分するので、ＡＰ：ＢＰ＝２：１です。
図のように、線分ＡＰ，ＢＰに対応する比を書き込みます。
図に比を書き込むと分かりますが、線分ＡＢに対応する比は、線分ＡＢを２：１に内分に内分したので２＋１＝３です。
比を書き込むとき、長さと区別するために丸や四角で囲んであげると分かりやすいです。また、比較している線分の比を同じ囲みにすることで、比較対象を簡単に区別できるのも利点です。
比は長さではないので、長さと混同しないように気を付けよう。
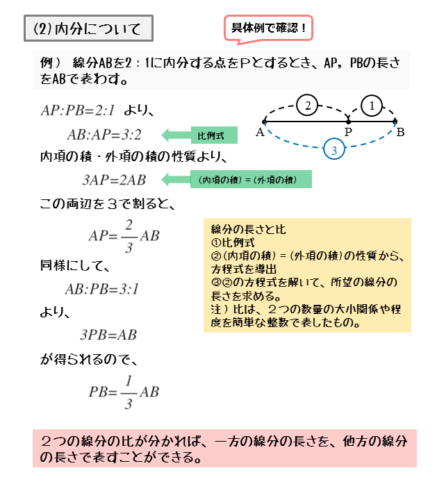
線分ＡＢに対応する比が分かると、ＡＢ：ＢＰ＝３：２という比例式を得ることができます。この比例式において、内項の積と外項の積の関係から、ＡＢを用いてＡＰを表すことができます。
線分ＡＰを線分ＡＢで表す
点 $P$ は線分 $AB$ を $2:1$ に内分するので
\begin{align*} &\quad AP：BP = 2:1 \end{align*}よって
\begin{align*} \quad AB：AP = 3:2 \end{align*}内項の積と外項の積の関係から
\begin{align*} \quad 3 \cdot AP = 2 \cdot AB \end{align*}よって
\begin{align*} \quad AP = \frac{2}{3} AB \end{align*}また、線分ＢＰについてもＡＢ：ＢＰ＝３：１という比例式を得ることができます。同じようにして、線分ＡＢを用いて線分ＢＰを表すことができます。
線分ＢＰを線分ＡＢで表す
点 $P$ は線分 $AB$ を $2:1$ に内分するので
\begin{align*} \quad AP：BP = 2:1 \end{align*}よって
\begin{align*} \quad AB：BP = 3:1 \end{align*}内項の積と外項の積の関係から
\begin{align*} \quad 3 \cdot BP = 1 \cdot AB \end{align*}よって
\begin{align*} \quad BP = \frac{1}{3} AB \end{align*}内分についてまとめると以下のようになります。
比例式について
ちなみに、比例式とは２つの比を等号（＝：イコール）でつないだ式のことです。
この比例式は等式です。しかし、このままではあまり使い道がありません。そこで、内項（内側の比）の積と外項（外側の比）の積は常に等しいという性質を利用します。
この性質を利用すると、長さが未知の線分についての方程式を導出することができます。導出された方程式を解くと、所望の線分の長さを求めることができます。
先ほどＡＰ，ＢＰの長さをＡＢで表しましたが、これは方程式を解いた後の式になります。
線分の外分
外分とは、線分の延長線上にある点で線分を分けることです。
一般に「線分ＡＢについて、ＡＱ：ＢＱ＝ｍ：ｎが成り立つとき、線分ＡＢは点Ｑによってｍ：ｎに外分される」と言います。
また、線分を外分する点のことを外分点と言います。外分点は線分上ではなく、線分の延長線上に存在します。
外分点で注意したいのは、内分点のときとは異なり、外分点は線分の左右どちらかにできるということです。
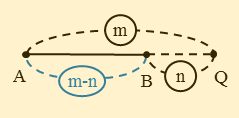
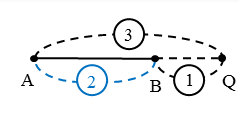
たとえば、点Ｑが線分ＡＢを２：１に外分する場合、ＡＱ：ＢＱ＝２：１です。ですから、外分点Ｑは比の小さいＢ側にできます。
外分点は２パターンあるので注意しよう。
外分後の線分の長さ
外分でも線分の長さを求める問題が出題されます。ただ、外分点の作図は意外と間違えやすいので、演習をこなしておきましょう。
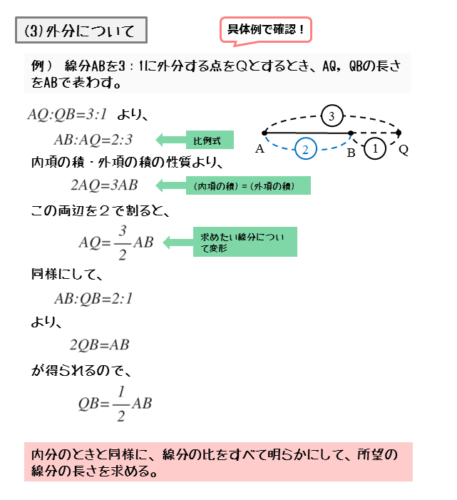
たとえば、線分ＡＢを３：１に外分する点をＱとするとき、線分ＡＱ，ＢＱの長さを線分ＡＢで表わしてみましょう。
線分ＡＢを外分点Ｑによって３：１に外分するので、ＡＱ：ＢＱ＝３：１です。
図のように、線分ＡＱ，ＢＱに対応する比を書き込みます。
比を書き込むと分かりますが、線分ＡＢに対応する比は、線分ＡＢを３：１に外分するので３－１＝２です。
線分ＡＢに対応する比が分かると、ＡＢ：ＡＱ＝２：３という比例式を得ることができます。この比例式において、内項の積と外項の積の関係から、ＡＢを用いてＡＱを表すことができます。
線分ＡＱを線分ＡＢで表す
点 $Q$ は線分 $AB$ を $3:1$ に外分するので
\begin{align*} \quad AQ:BQ = 3:1 \end{align*}よって
\begin{align*} \quad AB：AQ = 2:3 \end{align*}内項の積と外項の積の関係から
\begin{align*} \quad 2 \cdot AQ = 3 \cdot AB \end{align*}よって
\begin{align*} \quad AQ = \frac{3}{2} AB \end{align*}また、線分ＢＱについてもＡＢ：ＢＱ＝２：１という比例式を得ることができます。同じようにして、線分ＡＢを用いて線分ＢＱを表すことができます。
線分ＢＱを線分ＡＢで表す
点 $Q$ は線分 $AB$ を $3:1$ に外分するので
\begin{align*} \quad AQ:BQ = 3:1 \end{align*}よって
\begin{align*} \quad AB：BQ = 2:1 \end{align*}内項の積と外項の積の関係から
\begin{align*} \quad 2 \cdot BQ = 1 \cdot AB \end{align*}よって
\begin{align*} \quad AQ = \frac{1}{2} AB \end{align*}外分についてまとめると以下のようになります。
内分比や外分比を使いこなそう
内分比や外分比を使って線分の長さを求めるとき、そのたびごとに比例式を記述するのは面倒です。比の意味を知っていれば、作図だけで線分の長さを求めることができます。
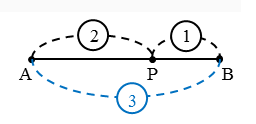
線分ＡＢを２：１に内分する例で求めた線分ＡＰ，ＢＰの長さについて考えてみましょう。
図から分かるように、線分ＡＢを２：１に内分するということは、ＡＢの長さを３として、ＡＰの長さを２、ＢＰの長さを１となるように分けるという意味です。
このとき、線分ＡＢ全体に対して、ＡＰの占める割合は２/３、ＢＰの占める割合は１/３になります。
この分数は、比例式から得た結果から分かるように、ＡＰ，ＢＰをＡＢで表したときの係数です。
線分ＡＰ，ＢＰの長さ
点 $P$ は線分 $AB$ を $2:1$ に内分するので
\begin{align*} \quad AP:BP = 2:1 \end{align*}よって
\begin{align*} &\quad AB：AP = 3:2 \\[ 7pt ] &\quad AB：BP = 3:1 \end{align*}したがって
\begin{align*} &\quad AP = \frac{2}{3} AB \\[ 7pt ] &\quad BP = \frac{1}{3} AB \end{align*}つまり、線分ＡＢ全体に占める割合が分かれば、線分ＡＢの長さと割合との積によって線分の長さを表せるということです。
（各線分の長さ）＝（各線分の全体に占める割合）×（全体の長さ）
毎回、比例式から線分の長さを求めるのは時間が掛かるので、慣れてきたら割合を使って一気に求めましょう。
なお、線分と内分比の関係は、教科書や参考書などでは公式化されています。ただ、作図しながら解いていれば、自然と覚えてしまう式なので、あまり心配しなくても良いでしょう。
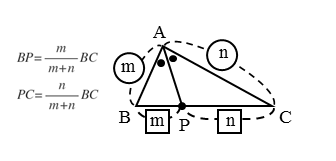
線分と内分比の関係
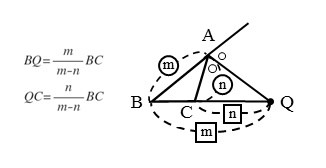
線分 $AB$ を $m:n$ に内分するとき
\begin{align*} \quad AP &= \frac{m}{m+n} AB \\[ 7pt ] BP &= \frac{n}{m+n} AB \end{align*}次は、角と線分の比との関係についてです。作図しながら学習しましょう。
三角形の内角の二等分線と比の関係
角の二等分線と比の関係を理解するには、中学で学習した平行線と線分の比の関係を知っておく必要があります。
△ＡＢＣにおいて、∠Ａの二等分線と辺ＢＣとの交点をＰとするとき、ＡＢ：ＡＣ＝ＢＰ：ＰＣが成り立ちます。
この比例式を導出してみましょう。
補助線を必要とするので、初見で導出できる人は少ないと思います。図形を扱う訓練になるので、ぜひチャレンジしてみて下さい。
平行線と角の関係を利用しよう
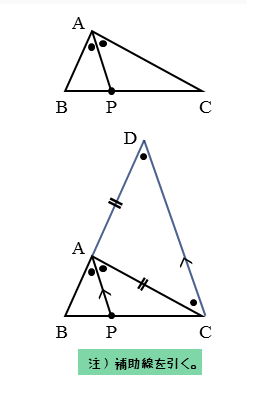
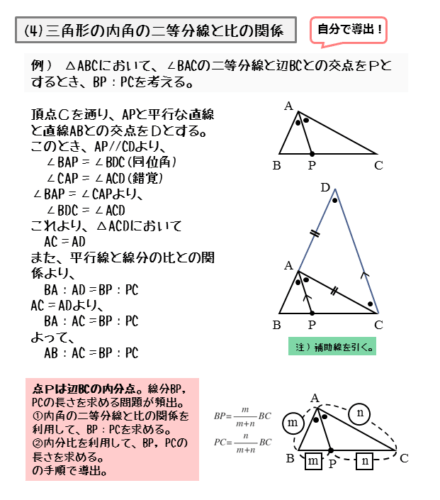
∠Ａの二等分線ＡＰに平行で点Ｃを通る直線を引き、この直線と辺ＡＢの延長線との交点をＤとします。
平行線と角の関係を利用すると、以下のような関係を得ることができます。
平行線と角の関係を利用する
$\angle BAC$ の二等分線と $BC$ の交点を $P$ とする。
また、点 $C$ を通り、$AP$ に平行な直線と、直線 $AB$ との交点を $D$ とする。
$AP \parallel CD$ より
\begin{align*} &\quad \angle ADC = \angle BAP \ \text{（同位角）} \\[ 7pt ] &\quad \angle ACD = \angle CAP \ \text{（錯角）} \end{align*}$\angle BAP = \angle CAP$ より
\begin{align*} \quad \angle ADC = \angle ACD \end{align*}これより $\triangle ACD$ は二等辺三角形になるので
\begin{align*} \quad AC = AD \end{align*}
平行線と角の関係を利用して、ＡＣ＝ＡＤを導くことがポイントです。
平行線と線分の比の関係を利用しよう
また、平行線と線分の比の関係を利用すると、以下のような関係を得ることができます。
平行線と線分の比の関係を利用する
$AP \parallel CD$ より
\begin{align*} \quad BA : AD = BP : PC \end{align*}この比例式と、先ほど証明したＡＣ＝ＣＤであることを利用すると、ＡＢ：ＡＣ＝ＢＰ：ＰＣを導出することができます。証明の例は以下のようになります。
以上のことから、三角形において内角の二等分線と比の関係から、対辺の内分比を求めることができるようになります。
角の二等分線と比の関係を内分比に絡めた問題は頻出なので、性質を上手に使いこなせるように演習しておきましょう。
三角形の外角の二等分線と比との関係
△ＡＢＣにおいて、∠Ａの外角の二等分線と辺ＢＣとの交点をＱとするとき、ＡＢ：ＡＣ＝ＢＱ：ＱＣという比例式が成り立ちます。
この比例式を導くときにも、補助線が必要になります。
平行線と角の関係を利用しよう
内角の二等分線と同じようにして補助線を書き込むことから始めます。
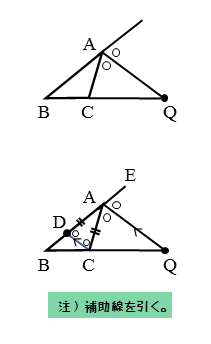
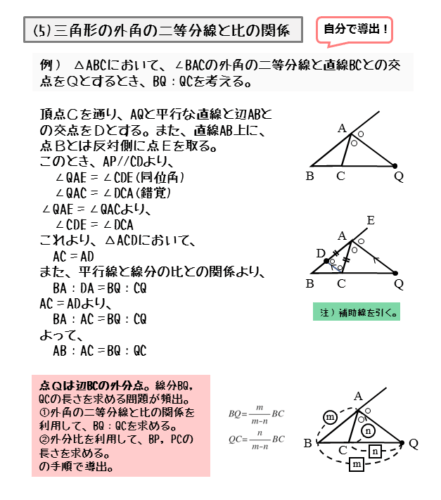
∠Ａの外角の二等分線ＡＱに平行で点Ｃを通る直線を引き、この直線と辺ＡＢとの交点をＤとします。なお、辺ＡＢの延長線上にＥを取ります。
平行線と角の関係を利用すると、以下のような関係を得ることができます。
平行線と角の関係を利用する
$\angle BAC$ の外角の二等分線と直線 $BC$ の交点を $Q$ とする。
この二等分線に平行で、点 $C$ を通る直線と辺 $AB$ との交点を $D$ とする。
また、直線 $AB$ 上に点 $B$ とは反対側にある点を $E$ とする。
$AQ \parallel CD$ より
\begin{align*} &\quad \angle ADC = \angle EAQ \ \text{（同位角）} \\[ 7pt ] &\quad \angle ACD = \angle CAQ \ \text{（錯角）} \end{align*}$\angle EAQ = \angle CAQ$ より
\begin{align*} \quad \angle ADC = \angle ACD \end{align*}これより $\triangle ACD$ は二等辺三角形になるので
\begin{align*} \quad AC = AD \end{align*}
内角のときと同じように、ＡＣ＝ＡＤを導くことがポイントです。
平行線と線分の比の関係を利用しよう
また、平行線と線分の比の関係を利用すると、以下のような関係を得ることができます。
平行線と線分の比の関係を利用する
$AQ \parallel CD$ より
\begin{align*} \quad AB : AD = QB : QC \end{align*}この比例式と、先ほどのＡＣ＝ＡＤであることを利用すると、ＡＢ：ＡＣ＝ＢＱ：ＱＣを導出することができます。証明の例は以下のようになります。
以上のことから、三角形において外角の二等分線と比の関係から、対辺の外分比を求めることができるようになります。
角の二等分線と比の学習内容をまとめると以下のようになります。図とセットにして、しっかり覚えましょう。
次は、角の二等分線と比の関係を利用して問題を解いてみましょう。