図形の性質|円周角について

今回は円周角について学習しましょう。
円周角についてはすでに中学で学習済みですが、高校では三角形に加えて四角形との関係も学習します。既習内容を確認しながら取り組んでいくと理解がより深まるでしょう。
また、「図形の性質」でもいくつかの定理や性質を学習したので、証明問題を扱うようになってきます。
積極的に取り組んで、論理的に記述する能力を向上させましょう。他の科目でもきっと役立つはずです。
記事の画像が見辛いときはクリックすると拡大できます。
円周角の定理とその定理の逆
この単元では、円周角の定理とその定理の逆について学習します。
円周角の定理は、中学で既に学習しましたが、次の2つの事柄が成り立つ定理です。
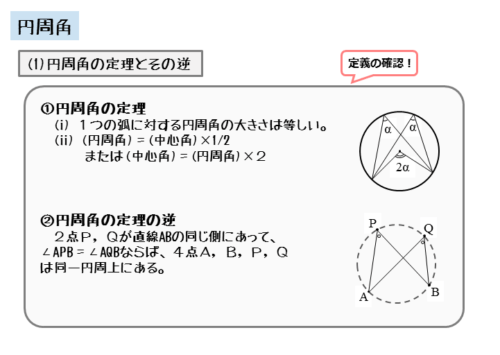
円周角の定理
- 1つの弧に対する円周角の大きさは等しい。
- 円周角は中心角の半分(1/2)である。
中学では、どちらも成り立つという前提で利用していただけです。ですから、本当に成り立つことを証明せよ、と言われると困る人は多いかもしれません。
それに対して高校では、これらの証明問題が出題されることがあるので、きちんと準備しておくことが望ましいでしょう。
円周角の定理の逆は次の事柄が成り立つ定理です。こちらは四角形を扱った問題でよく出題されます。
円周角の定理の逆
2点P,Qが直線ABの同じ側にあって、∠APB=∠AQBが成り立つとき、4点A,B,P,Qが同一円周上にある。
円周角の定理とその逆の関係を整理してみましょう。ちゃんと逆の関係になっていることが分かります。
円周角の定理とその逆の関係
円周上に4点がある ⇒ 円周角が等しい(円周角の定理)
4点があり、(円周角に相当する)角の大きさが等しくなる ⇒ 4点は同一円周上にある(円周角の定理の逆)
はじめに円が与えられていない場合、円周角の定理の逆が成り立つことに全く気付かないことがよくあります。多めに演習をこなしておきましょう。
円周角の定理を証明しよう
円周角の定理
- 1つの弧に対する円周角の大きさは等しい。
- 円周角は中心角の半分(1/2)である。
まず「円周角は中心角の半分(1/2)である。」ことを証明してみましょう。「1つの弧に対する円周角の大きさは等しい」ことの証明を後に回した方が易しくなります。
中心をOとする円の周上に3点A,B,Pがあるとします。このとき、円周角∠APBができます。
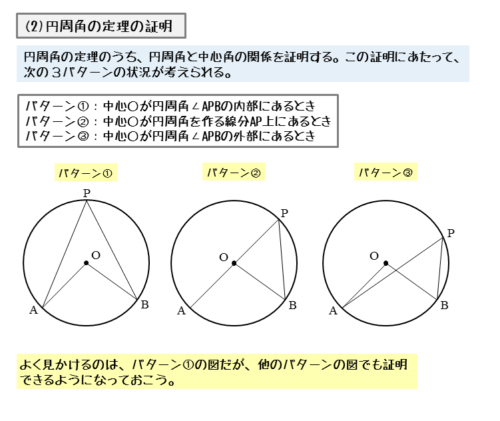
円周角∠APBができる位置は、点Pの位置によって異なります。中心Oの位置に注目して、3通りのパターンに場合分けして証明します。
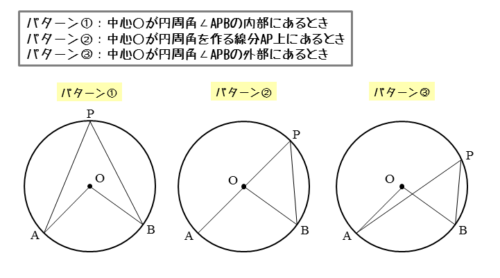
「円周角は中心角の半分(1/2)である」ことの証明は3パターンの場合分け
- 中心Oが円周角∠APBの内部にあるとき
- 中心Oが円周角を作る線分AP上にあるとき
- 中心Oが円周角∠APBの外部にあるとき
3パターンありますが、証明の流れは大筋で変わりません。
また、既習内容で証明できるので、良い復習になります。ぜひ挑戦してみて下さい。
中心Oが円周角∠APBの内部にあるとき
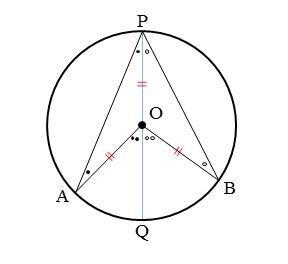
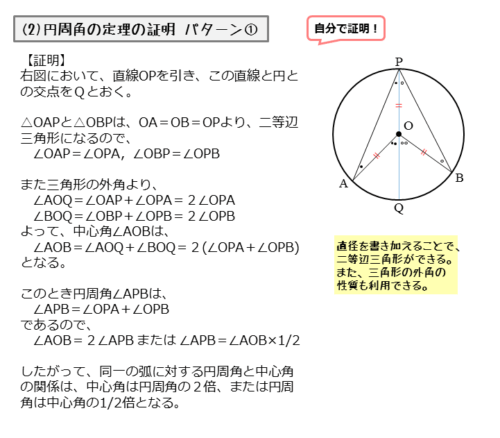
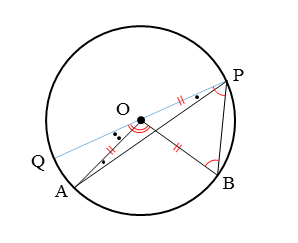
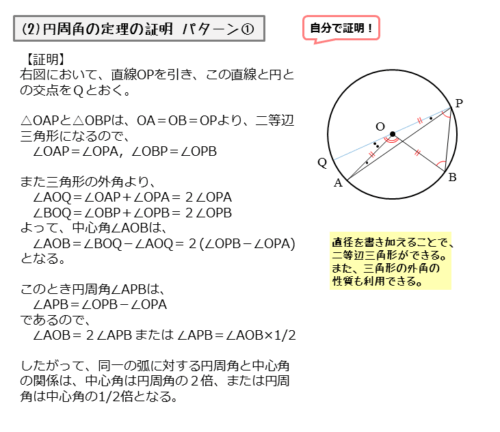
中心Oが円周角∠APBの内部にあるとき、円周角は中心角の半分(1/2)であることを証明します。
補助線として直線OPを引き、直線OPと円との交点をQとします。
直線OPを引いたことで、線分OA,OB,OPが半径に等しくなりました。
このことから、△OAP,△OBPは二等辺三角形になります。
二等辺三角形の性質を利用すると、角の関係が得られます。
二等辺三角形の性質を利用する
\begin{align*} \quad OA = OB = OP \end{align*}より、$\triangle OAP \ , \ \triangle OBP$ は二等辺三角形。
よって
\begin{align*} &\quad \angle OAP = \angle OPA \quad \cdots \text{①} \\[ 7pt ] &\quad \angle OBP = \angle OPB \quad \cdots \text{②} \end{align*}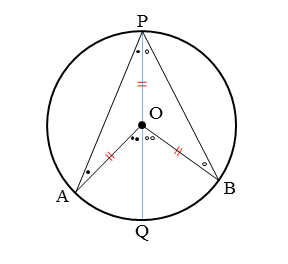
次は三角形の外角を利用します。
三角形の外角を利用する
\begin{align*} &\vdots \\[ 7pt ] \quad \angle OBP &= \angle OPB \quad \cdots \text{②} \end{align*}三角形の外角より
\begin{align*} &\quad \angle AOQ = \angle OAP + \angle OPA \\[ 7pt ] &\quad \angle BOQ = \angle OBP + \angle OPB \end{align*}これと①,②より
\begin{align*} &\quad \angle AOQ = 2 \angle OPA \quad \cdots \text{③} \\[ 7pt ] &\quad \angle BOQ = 2 \angle OPB \quad \cdots \text{④} \end{align*}
さいごに中心角∠AOBを円周角∠APBで表します。
中心角∠AOBを円周角∠APBで表す
\begin{align*} &\vdots \\[ 7pt ] \angle AOB &= \angle AOQ + \angle BOQ \\[ 7pt ] &= 2 \angle OPA + 2 \angle OPB \quad \text{(③,④より)} \\[ 7pt ] &= 2 ( \angle OPA + \angle OPB ) \\[ 7pt ] &= 2 \angle APB \\[ 7pt ] \therefore \ \angle APB &= \frac{1}{2} \angle AOB \end{align*}
以上のことから、中心Oが円周角∠APBの内部にあるとき、円周角は中心角の半分(1/2)であるので、円周角の定理は成り立ちます。
証明のポイントは、補助線として引いた直線OP(直径)です。
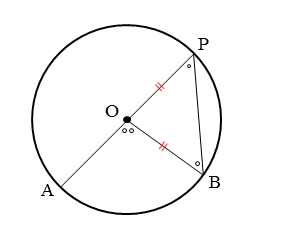
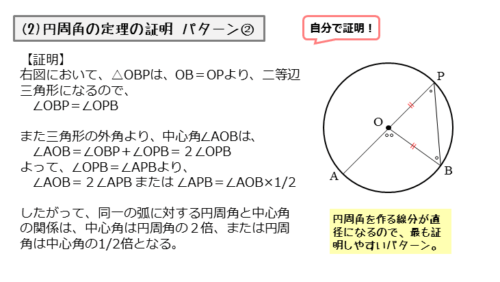
中心Oが円周角を作る線分AP上にあるとき
中心Oが円周角を作る線分AP上にあるとき、円周角は中心角の半分(1/2)であることを証明します。
パターン①と同じ流れで証明します。△OBPが二等辺三角形になることを利用します。
二等辺三角形の性質を利用する
\begin{align*} \quad OB = OP \end{align*}より、$\triangle OBP$ は二等辺三角形。
よって
\begin{align*} \quad \angle OBP = \angle OPB \quad \cdots \text{①} \end{align*}次は三角形の外角を利用します。∠AOBは、△OBPの外角ですが、中心角でもあることに注意します。
三角形の外角を利用する
\begin{align*} &\vdots \\[ 7pt ] \quad \angle OBP &= \angle OPB \quad \cdots \text{①} \end{align*}三角形の外角より
\begin{align*} \quad \angle AOB = \angle OBP + \angle OPB \end{align*}これと①より
\begin{align*} \quad \angle AOB &= 2 \angle OPB \\[ 7pt ] \quad \angle OPB &= \frac{1}{2} \angle AOB \\[ 7pt ] \therefore \ \angle APB &= \frac{1}{2} \angle AOB \end{align*}以上のことから、中心Oが円周角を作る線分AP上にあるとき、円周角は中心角の半分(1/2)であるので、円周角の定理は成り立ちます。
3つのパターンの中で最も簡単な証明になるので、証明の流れを把握するのに利用しましょう。
中心Oが円周角∠APBの外部にあるとき
中心Oが円周角∠APBの外部にあるとき、円周角は中心角の半分(1/2)であることを証明します。
補助線として直線OPを引き、直線OPと円との交点をQとします。少し複雑な図になりますが、パターン①と同じ流れで証明します。
直線OPを引いたことで、線分OA,OB,OPは半径に等しくなりました。
このことから、△OAP,△OBPは二等辺三角形になります。
二等辺三角形の性質を利用します。
二等辺三角形の性質を利用する
\begin{align*} \quad OA = OB = OP \end{align*}より、$\triangle OAP \ , \ \triangle OBP$ は二等辺三角形。
よって
\begin{align*} &\quad \angle OAP = \angle OPA \quad \cdots \text{①} \\[ 7pt ] &\quad \angle OBP = \angle OPB \quad \cdots \text{②} \end{align*}次は三角形の外角を利用します。
三角形の外角を利用する
\begin{align*} &\vdots \\[ 7pt ] \quad \angle OBP &= \angle OPB \quad \cdots \text{②} \end{align*}三角形の外角より
\begin{align*} &\quad \angle AOQ = \angle OAP + \angle OPA \\[ 7pt ] &\quad \angle BOQ = \angle OBP + \angle OPB \end{align*}これと①,②より
\begin{align*} &\quad \angle AOQ = 2 \angle OPA \quad \cdots \text{③} \\[ 7pt ] &\quad \angle BOQ = 2 \angle OPB \quad \cdots \text{④} \end{align*}さいごに中心角∠AOBを円周角∠APBで表します。
中心角∠AOBを円周角∠APBで表す
\begin{align*} &\vdots \\[ 7pt ] \angle AOB &= \angle BOQ – \angle AOQ \\[ 7pt ] &= 2 \angle OPB – 2 \angle OPA \quad \text{(③,④より)} \\[ 7pt ] &= 2 ( \angle OPB – \angle OPA ) \\[ 7pt ] &= 2 \angle APB \\[ 7pt ] \therefore \ \angle APB &= \frac{1}{2} \angle AOB \end{align*}以上のことから、中心Oが円周角∠APBの外部にあるとき、円周角は中心角の半分(1/2)であるので、円周角の定理は成り立ちます。
補助線として直線OP(直径)を引くのはパターン①と同じです。異なるのは、中心角∠AOBを円周角∠APBで表すとき、外角の和ではなく、外角の差になることです。注意しましょう。
どのパターンでも二等辺三角形を上手に利用しています。二等辺三角形があれば、底角や外角を利用して、円周角と中心角の関係を導出することができます。
1つの弧に対する円周角の大きさは等しいことの証明
「1つの弧に対する円周角の大きさは等しい」ことの証明は「円周角は中心角の半分(1/2)である」ことの証明を利用します。
円周角∠APBは、中心Oとの関係によって3パターンに場合分けしましたが、すべての場合で中心角∠AOBを用いて表されます。
以上のことから、円周角の大きさは、点Pがどの位置にあっても中心角の半分で表され、すべて等しくなります。
定理の証明は、過去のセンター試験で何度も出題されている。定理の証明方法を知っておくことは入試対策になるので、暗記で済ませないようにしよう。
次は円周角の定理の逆を証明してみましょう。
円周角の定理の逆を証明しよう
円周角の定理の逆
2点P,Qが直線ABの同じ側にあって、∠APB=∠AQBが成り立つとき、4点A,B,P,Qが同一円周上にある。
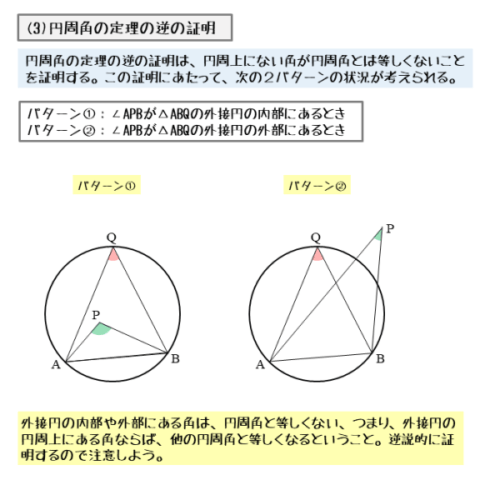
円周角の定理の逆の証明は、逆説的に行うので、初見では難しいかもしれません。次の2パターンの場合に分けて証明します。
「円周角の定理の逆」の証明は2パターンの場合分け
- 点Pが△ABQの外接円の内部にあるとき
- 点Pが△ABQの外接円の外部にあるとき
△ABQの外接円に対する点Pの位置によって場合分けします。
点Pが△ABQの外接円の周上にあれば、円周角の定理より、∠APB=∠AQB が成り立つのは明らかです。
点Pが△ABQの外接円の内部にあるとき
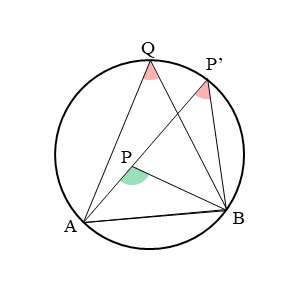
図のように、△ABQの外接円を考えます。
3点A,B,Qは円周上にあるので、∠AQBは円周角です。
また、点Pは外接円の内部にあるので、∠APBは円周角ではありません。
このとき、直線APと外接円との交点をP’とすると、∠AP’Bは円周角になります。
このような図形において、∠APBと∠AQBの関係を調べます。
∠APBと∠AQBの関係を調べる
点 $P’$ は円周上の点であるので
\begin{align*} \quad \angle AP’B = \angle AQB \end{align*}また、三角形の外角より
\begin{align*} \quad \angle APB = \angle AP’B + \angle P’BP \end{align*}であるので
\begin{align*} \quad \angle APB \gt \angle AP’B \end{align*}よって
\begin{align*} \quad \angle APB \gt \angle AQB \end{align*}以上のことから、点Pが外接円の内部にあるとき、∠APB≠∠AQBであることを証明できました。
点Pが△ABQの外接円の外部にあるとき
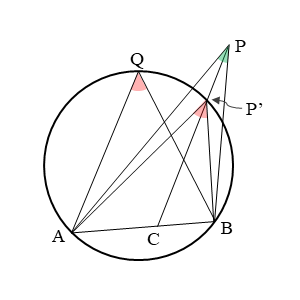
図のように、△ABQの外接円を考えます。
3点A,B,Qは円周上にあるので、∠AQBは円周角です。
また、点Pは外接円の外部にあるので、∠APBは円周角ではありません。
このとき、辺AB上に2点A,Bとは異なる点Cをとります。そして、直線CPと外接円との交点をP’とすると、∠AP’Bは円周角になります。
このような図形において、∠APBと∠AQBの関係を調べます。
∠APBと∠AQBの関係を調べる
三角形の外角より
\begin{align*} &\quad \angle APC = \angle AP’C \ – \angle PAP’ \\[ 7pt ] &\quad \angle CPB = \angle CP’B \ – \angle PBP’ \end{align*}また
\begin{align*} \quad \angle APB = \angle APC + \angle CPB \end{align*}であるので
\begin{align*} &\quad \angle APB = ( \angle AP’C + \angle CP’B ) \ – ( \angle PAP’ + \angle PBP’ ) \\[ 7pt ] &\quad \angle APB = \angle AP’B \ – ( \angle PAP’ + \angle PBP’ ) \end{align*}これより
\begin{align*} \quad \angle APB \lt \angle AP’B \end{align*}よって
\begin{align*} \quad \angle APB \lt \angle AQB \end{align*}以上のことから、点Pが外接円の外部にあるとき、∠APB≠∠AQBであることを証明できました。
どちらの場合も∠APB=∠AQBとはなりません。つまり、∠APB=∠AQBとなるには点Pも△ABQの外接円の周上になければならないということです。
したがって、2点P,Qが直線ABの同じ側にあって、∠APB=∠AQBが成り立てば、4点A,B,P,Qが同一円周上にあると言えます。
次は円周角の定理などを扱った問題を解いてみましょう。