数学２
今回は、２次方程式の係数と２つの解の符号について学習しましょう。これまでの学習で、２次方程式の係数が、２つの解と関わりがあることが分かりました。ここでは、この関係を２つの解の符号と絡めて学習します。
２次方程式の実数解の符号
２次方程式が２つの実数解をもつとき、これらの符号からどのような条件が成り立つのかを考えてみましょう。
２つの実数解が取り得る符号の組み合わせは３通りあります。
２つの実数解が取り得る符号の組み合わせは３通り
- ２つの実数解の符号がともに正
- ２つの実数解の符号がともに負
- ２つの実数解が異符号
それぞれの場合について、どのような条件が成り立つのかを考えます。
２つの実数解の符号がともに正のとき
２次方程式の解を考えるとき、２次関数のグラフを用いると視覚化されて理解しやすくなります。
２次方程式は、２次関数においてｙ＝０のときの式です。この２次方程式を解くと、ｙ＝０のときのｘの値が得られます。このときのｘの値は、２次関数のグラフとｘ軸との共有点のｘ座標です。
つまり、２次方程式を解くということは、グラフとｘ軸との共有点のｘ座標を求めるということです。ですから、グラフがｘ軸と共有点をもてば、２次方程式は実数解をもつことになります。たとえば、グラフがｘ軸と２点で交わるならば、２次方程式は異なる２つの実数解をもちます。
２つの実数解の符号がともに正であるということは、２つの共有点のｘ座標がともに正であるということです。図示すると以下のようになります。
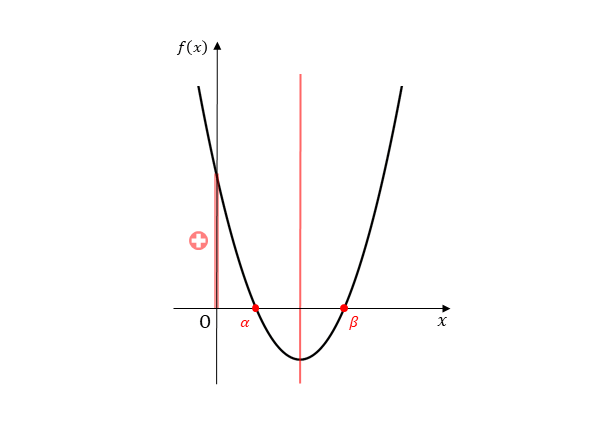２つの実数解の符号がともに正のとき ２次関数のグラフは、図のようにｘ軸の正の部分と２点で交わります。このようにグラフがｘ軸と共有点をもつためには、以下のような条件が成り立つ必要があります。
２つの実数解の符号がともに正のとき1⃣
\begin{align*}
&\text{$2$ 次方程式} \\[ 5pt ]
&\quad ax^{\scriptsize{2}}+bx+c=0 \\[ 5pt ]
&\text{の $2$ つの解を} \\[ 5pt ]
&\quad \alpha \ , \ \beta \\[ 5pt ]
&\text{とする。} \\[ 5pt ]
&\text{また、判別式を} \\[ 5pt ]
&\quad D=b^{\scriptsize{2}}-4ac \\[ 5pt ]
&\text{とする。} \\[ 5pt ]
&\text{$\alpha \gt 0$ かつ $\beta \gt 0$ となるには} \\[ 5pt ]
&\quad f(x)=ax^{\scriptsize{2}}+bx+c \quad (a \gt 0) \\[ 5pt ]
&\text{のグラフと $x$ 軸との共有点の関係から} \\[ 5pt ]
&\quad \left\{
\begin{array}{l}
D \geqq 0 \\[ 5pt ]
\text{軸} \ -\frac{b}{2a} \gt 0 \qquad \cdots \text{①} \\[ 5pt ]
f(0) \gt 0
\end{array}
\right. \\[ 5pt ]
&\text{が成り立てばよい。}
\end{align*}
この条件は２次関数のグラフとｘ軸との位置関係から得られます。図と併せて考えると分かりやすいでしょう。
この単元では、解と係数との関わりを中心に学習しています。ですから、２つの実数解を用いて条件を書き出してみましょう。以下のようになります。
２つの実数解の符号がともに正のとき2⃣
\begin{align*}
&\text{$2$ 次方程式} \\[ 5pt ]
&\quad ax^{\scriptsize{2}}+bx+c=0 \\[ 5pt ]
&\text{の $2$ つの解を} \\[ 5pt ]
&\quad \alpha \ , \ \beta \\[ 5pt ]
&\text{とする。} \\[ 5pt ]
&\text{また、判別式を} \\[ 5pt ]
&\quad D=b^{\scriptsize{2}}-4ac \\[ 5pt ]
&\text{とする。} \\[ 5pt ]
&\text{$\alpha \gt 0$ かつ $\beta \gt 0$ となるには、} \\[ 5pt ]
&\quad \left\{
\begin{array}{l}
D \geqq 0 \\[ 5pt ]
\alpha+\beta \gt 0 \qquad \cdots \text{②} \\[ 5pt ]
\alpha \beta \gt 0
\end{array}
\right. \\[ 5pt ]
&\text{が成り立てばよい。}
\end{align*}
３つの条件が必要ですが、それぞれの条件で言えることをきちんと理解しておきましょう。
たとえば、判別式の条件だけでは、実数解の個数しか決定できません。２つの実数解の符号を決定するには、２つの実数解の和と積の条件が必要です。
２つの実数解の符号がともに正であるためには、２つの実数解の和と積がともに正でなければなりません。
２つの条件の違い
２次関数のグラフを用いたときと、２次方程式の２つの実数解で考えたときの条件を整理すると以下のようになります。
２つの条件の違いを比較する1⃣
\begin{align*}
&\text{$2$ 次関数のグラフから得られる条件} \\[ 5pt ]
&\quad \left\{
\begin{array}{l}
D \geqq 0 \\[ 5pt ]
\text{軸} \ -\frac{b}{2a} \gt 0 \qquad \cdots \text{①} \\[ 5pt ]
f(0) \gt 0
\end{array}
\right. \\[ 10pt ]
&\text{$2$ 次方程式から得られる条件} \\[ 5pt ]
&\quad \left\{
\begin{array}{l}
D \geqq 0 \\[ 5pt ]
\alpha+\beta \gt 0 \qquad \cdots \text{②} \\[ 5pt ]
\alpha \beta \gt 0
\end{array}
\right.
\end{align*}
２つの条件①，②は、全く別物のように感じるかもしれませんが、そうでもありません。もう少し詳しく調べてみると、２つの条件が等価であることが分かります。
２つの条件の違いを比較する2⃣
\begin{align*}
&\text{軸の条件から} \\[ 5pt ]
&\quad -\frac{b}{2a} \gt 0 \quad \text{すなわち} \quad -\frac{b}{a} \gt 0 \\[ 7pt ]
&\text{２つの実数解の和の条件から} \\[ 5pt ]
&\quad \alpha+\beta \gt 0 \quad \text{すなわち} \quad -\frac{b}{a} \gt 0 \\[ 7pt ]
&\text{となり、２つの条件は等価である。} \\[ 10pt ]
&\text{グラフとｙ軸との関係から} \\[ 5pt ]
&\quad f(0) \gt 0 \quad \text{すなわち} \quad c \gt 0 \\[ 7pt ]
&\text{２つの実数解の積の条件から} \\[ 5pt ]
&\quad \alpha \beta \gt 0 \quad \text{すなわち} \quad \frac{c}{a} \gt 0 \\[ 7pt ]
&\text{$a \gt 0$ であるので} \\[ 5pt ]
&\quad c \gt 0 \\[ 7pt ]
&\text{となり、こちらの条件も等価である。}
\end{align*}
条件②では、２つの実数解の和と積が出てくるので、解と係数の関係を利用します。
条件の見た目は違っていますが、最終的には同じ条件が得られるので実質的に等価です。ですから、２次方程式の２つの実数解の和と積を用いて、２つの実数解の符号が成り立つ条件を考えても構わないのです。
そうは言っても、グラフを用いて視覚化すると、条件を明確にイメージできる利点があります。基本的には図示しながら考えましょう。
２つの実数解の符号がともに正となるための条件
\begin{align*}
&\quad \text{$\alpha \gt 0$ かつ $\beta \gt 0$} \quad \Longleftrightarrow \quad D \geqq 0 \ , \ \alpha+\beta \gt 0 \ , \ \alpha \beta \gt 0 \\[ 7pt ]
&\text{ただし、$2$ 次方程式 $ax^{\scriptsize{2}}+bx+c=0$ の $2$ つの解を $\alpha \ , \ \beta$} \\[ 5pt ]
&\text{判別式を $D=b^{\scriptsize{2}}-4ac$ とする。}
\end{align*}
グラフの様子もセットで覚えておきましょう。
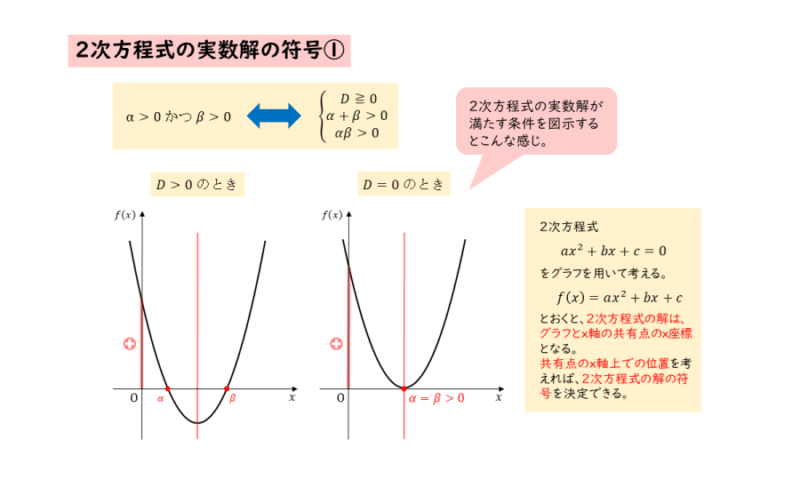実数解の符号が正であるときのグラフと条件 ２つの実数解の符号がともに負のとき
残りの符号の組合せの場合も同じ要領です。２次関数のグラフを図示すると、以下のようになります。
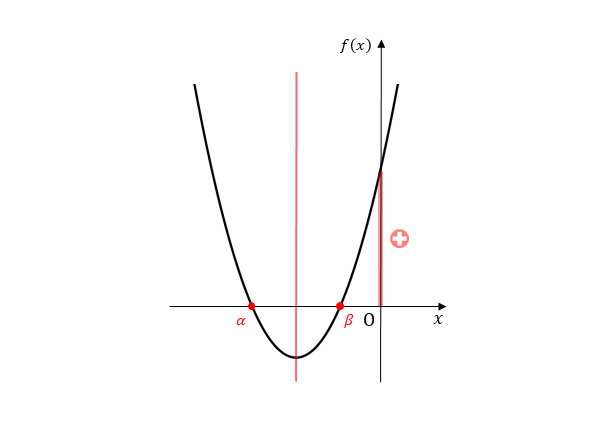２つの実数解の符号がともに負のとき ２次関数のグラフを用いたときと、２次方程式の２つの実数解で考えたときの条件を整理すると以下のようになります。
２つの実数解がともに負のとき
\begin{align*}
&\text{$\alpha \lt 0$ かつ $\beta \lt 0$ となるための条件は以下の通り。} \\[ 5pt ]
&\text{$2$ 次関数のグラフから得られる条件} \\[ 5pt ]
&\quad \left\{
\begin{array}{l}
D \geqq 0 \\[ 5pt ]
\text{軸} \ -\frac{b}{2a} \lt 0 \qquad \cdots \text{③} \\[ 5pt ]
f(0) \gt 0
\end{array}
\right. \\[ 10pt ]
&\text{$2$ 次方程式から得られる条件} \\[ 5pt ]
&\quad \left\{
\begin{array}{l}
D \geqq 0 \\[ 5pt ]
\alpha+\beta \lt 0 \qquad \cdots \text{④} \\[ 5pt ]
\alpha \beta \gt 0
\end{array}
\right.
\end{align*}
２つの実数解の符号がともに負であるためには、２つの実数解の和が負、かつ積が正でなければなりません。２つの条件③，④は、見た目は異なっていてもやはり等価です。
２つの実数解がともに負となるための条件
\begin{align*}
&\quad \text{$\alpha \lt 0$ かつ $\beta \lt 0$} \quad \Longleftrightarrow \quad D \geqq 0 \ , \ \alpha+\beta \lt 0 \ , \ \alpha \beta \gt 0 \\[ 7pt ]
&\text{ただし、$2$ 次方程式 $ax^{\scriptsize{2}}+bx+c=0$ の $2$ つの解を $\alpha \ , \ \beta$} \\[ 5pt ]
&\text{判別式を $D=b^{\scriptsize{2}}-4ac$ とする。}
\end{align*}
グラフもセットで覚えましょう。
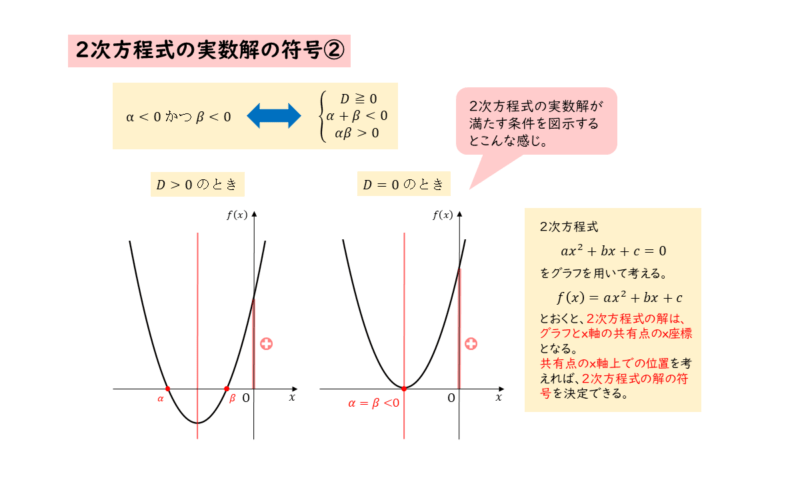実数解の符号が負であるときのグラフと条件 ２つの実数解の符号が異符号の場合
２つの実数解の符号が異符号の場合はこれまでよりも条件が少なくなりますが、同じ要領です。２次関数のグラフを図示すると、以下のようになります。
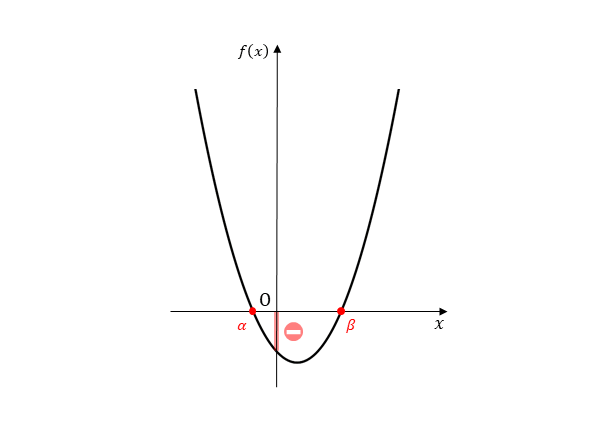２つの実数解の符号が異符号のとき ２次関数のグラフを用いたときと、２次方程式の２つの実数解で考えたときの条件を整理すると以下のようになります。
２つの実数解が異符号のとき
\begin{align*}
&\text{$\alpha$ と $\beta$ の符号が異符号となるための条件は以下の通り。} \\[ 5pt ]
&\text{$2$ 次関数のグラフから得られる条件} \\[ 5pt ]
&\quad f(0) \lt 0 \quad \cdots \text{⑤} \\[ 10pt ]
&\text{$2$ 次方程式から得られる条件} \\[ 5pt ]
&\quad \alpha \beta \lt 0 \quad \cdots \text{⑥}
\end{align*}
２つの実数解の符号が異符号であるためには、２つの実数解の積が負でなければなりません。和については、正負どちらとも言えないので一意に決まりません。
また、判別式の条件がないのは、２つの条件⑤，⑥が成り立てば、２次方程式が２つの実数解をもつ条件（Ｄ＞０）を満たすからです。このことはグラフを見れば明らかです。
もちろん、２つの条件⑤，⑥はやはり等価な条件となります。
２つの実数解が異符号となるための条件
\begin{align*}
&\quad \text{$\alpha$ と $\beta$ の符号が異符号} \quad \Longleftrightarrow \quad \alpha \beta \lt 0 \\[ 7pt ]
&\text{ただし、$2$ 次方程式 $ax^{\scriptsize{2}}+bx+c=0$ の $2$ つの解を $\alpha \ , \ \beta$ とする。}
\end{align*}
グラフもセットで覚えましょう。
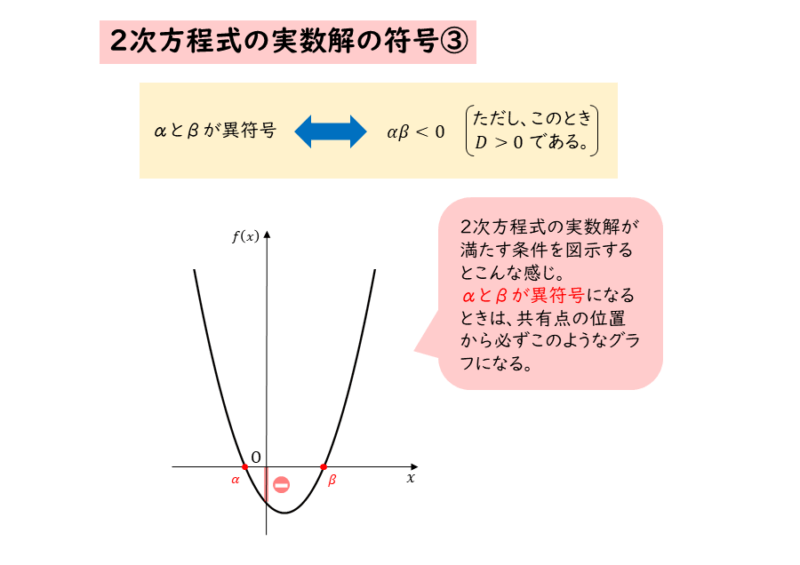実数解の符号が異符号であるときのグラフと条件 ２つの実数解の符号の組み合わせとその条件のまとめ
３通りの組み合わせについて、まとめると以下のようになります。
２つの実数解の符号の組み合わせとその条件
\begin{align*}
&\text{$2$ 次方程式 $ax^{\scriptsize{2}}+bx+c=0$ の $2$ つの解を $\alpha \ , \ \beta$ とする。} \\[ 5pt ]
&\text{また、判別式を $D=b^{\scriptsize{2}}-4ac$ とする。} \\[ 5pt ]
&\text{[１] $\quad \alpha \gt 0$ かつ $\beta \gt 0$} \quad \Longleftrightarrow \quad D \geqq 0 \ , \ \alpha+\beta \gt 0 \ , \ \alpha \beta \gt 0 \\[ 7pt ]
&\text{[２] $\quad \alpha \lt 0$ かつ $\beta \lt 0$} \quad \Longleftrightarrow \quad D \geqq 0 \ , \ \alpha+\beta \lt 0 \ , \ \alpha \beta \gt 0 \\[ 7pt ]
&\text{[３] $\quad \alpha$ と $\beta$ の符号が異符号} \quad \Longleftrightarrow \quad \alpha \beta \lt 0 \\[ 7pt ]
&\text{（[３]のとき、$D \gt 0$ が成り立つので、判別式の条件は不要。）}
\end{align*}
２次方程式の２つの実数解の符号についての問題では、判別式と２つの実数解の和と積から条件を導きます。
２つの実数解の和と積は、言い換えると解と係数の関係です。解と係数の関係を利用するので、係数や定数項についての式を導くことができます。
次は、２次方程式の係数と２つの解の符号を扱った問題を実際に解いてみましょう。
