場合の数|組合せについて

今回は、組合せについて学習しましょう。場合の数を考えるとき、順列か組合せのどちらかを使う場合がほとんどです。
組合せは順列の考え方がベースになっています。順列についての知識が定着していない人はもう一度確認しておきましょう。そして、順列との違いをしっかり理解し、使い分けできるようにしておきましょう。
記事の画像が見辛いときはクリックすると拡大できます。
組合せの定義
組合せとは、いくつかの異なるものから希望の数だけ選んだものや選ぶことです。このような場合、選んだものの並びは考慮されません。
たとえば、A,B,CとB,A,Cは、並びが異なっていても同じものとして扱います。この点が、並ぶ順番が変わると別物として扱う順列とは異なるところです。
組合せの総数は、C(combinationまたはchooseの頭文字)という記号を使って表されます。一般に、以下のように定義されています。
組合せの総数
異なる $n$ 個から $r$ 個を選ぶ(取る)ときの組合せの総数
\begin{align*} \quad {}_n \mathrm{ C }_r = \frac{{}_n \mathrm{ P }_r}{r!} \end{align*}ただし
\begin{align*} &\quad {}_n \mathrm{ C }_0 = 1 \\[ 7pt ] &\quad {}_n \mathrm{ C }_n = 1 \end{align*}また、組合せの総数は以下のような性質をもちます。
組合せの総数の性質
異なる $n$ 個から $r$ 個を選ぶ(取る)ときの組合せの総数がもつ性質
\begin{align*} \quad {}_n \mathrm{ C }_r = {}_n \mathrm{ C }_{n-r} \end{align*}詳細については後述します。これまでのまとめです。
組合せと順列の違いを理解しよう
組合せと順列の関係
組合せの総数は、定義から分かるように、順列の総数から導出されます。具体例で考えてみましょう。
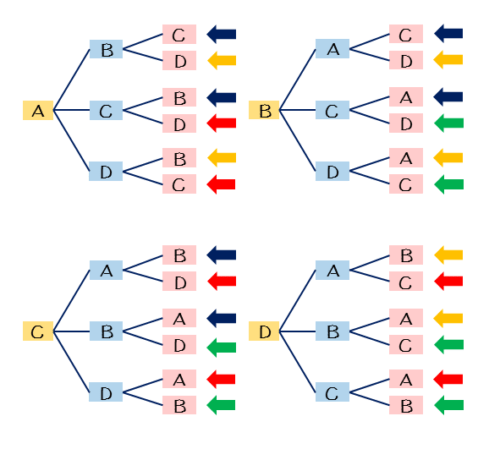
たとえば、4種類のA,B,C,Dから3種類を選ぶときの選び方、つまり組合せの総数はいくつになるでしょうか。とりあえず、今までと同じ要領で樹形図を書きます。
この樹形図では、考え得る候補を左から順に書き並べています。ですから、並びが変われば別物として扱っています。このままだと、順列の総数になってしまいます。
組合せの場合、並ぶ順序を考慮しません。もし、選ばれたアルファベットが3つとも同じであれば、同じ選び方として扱わなければなりません。これを踏まえて同じ並び(同色の矢印)を調べていきます。
1つの組合せに注目すると、同じものと見なせるものが他に5通りあります。
つまり、1つの組合せについて、6通りの並びが同じ選び方と見なせます。「6通り」となったのは、3つのアルファベットの並べ方(順列の総数)が3!(=6)通りだからです。
以上のことから、順列の総数は、組合せのそれぞれについて、並べ方が順列の数(6通り)ずつあることから得られた場合の数と考えることができます。
順列の総数は、組合せのそれぞれについて、並べ方が順列の数ずつあることを利用して求めることができる。
重複の原因を取り除こう
重複の原因は、樹形図を書くときに並びの違いまで考慮したからです。別の言い方をすれば、1つの組合せについて、その並べ方まで考慮したからです。
4種類から3種類を取って並べたので、順列の総数は4P3通りです。そして、重複ぶんは組合せのそれぞれについて3!(=6)通りずつあります。この重複ぶんを取り除くために除算すると、組合せの総数が得られます。
順列の総数から重複を除けば組合せの総数
異なる $4$ 個から $3$ 個を選ぶ(取る)ときの組合せの総数は、異なる $4$ 個から $3$ 個を取って並べるときの順列の総数から重複ぶん $3!$ を除けばよいので
\begin{align*} \quad {}_4 \mathrm{ C }_3 &= \frac{{}_4 \mathrm{ P }_3}{3!} \\[ 7pt ] &= \frac{4 \cdot 3 \cdot 2}{3 \cdot 2 \cdot 1} \\[ 7pt ] &= 4 \end{align*}これまでのまとめです。
組合せの総数
先ほどの具体例から分かるように、順列の総数は、組合せのそれぞれについて順列を考えた場合の数だと解釈することができました。
一般化すれば、異なるn個からr個取って並べるときの順列の総数nPrは、異なるn個からr個を選ぶ組合せの総数nCr通りのそれぞれについて、r!通りの並べ方を考えたときの場合の数となります。
この関係から、組合せの総数を導出することができます。
順列の総数から重複を除けば組合せの総数(一般化)
異なる $n$ 個から $r$ 個を選ぶ(取る)ときの組合せの総数は、異なる $n$ 個から $r$ 個を取って並べるときの順列の総数から重複ぶん $r!$ を除いたものに等しい。
言い換えると、異なる $n$ 個から $r$ 個を取って並べるときの順列の総数は、異なる $n$ 個から $r$ 個を選ぶ(取る)ときの組合せのそれぞれについて、並べ方が $r!$ 通りずつあるのに等しい。
\begin{align*} \quad {}_n \mathrm{ P }_r &= {}_n \mathrm{ C }_r \times r! \\[ 10pt ] \therefore \ {}_n \mathrm{ C }_r &= \frac{{}_n \mathrm{ P }_r}{r!} \end{align*}組合せの樹形図を書くコツ
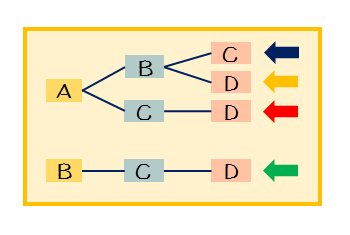
樹形図を書いて組合せを調べるとき、今まで通りだと重複ぶんを含んでしまいます。先ほどの樹形図から重複ぶんを取り除くと、以下のような樹形図になります。
このような組合せだけが分かる樹形図を書くにはコツがあります。
組合せの樹形図を書くコツ
- アルファベット順(A,B,C,…)に書く。
- アルファベット順に書くとき、前のものは後のものより右側に書かない。
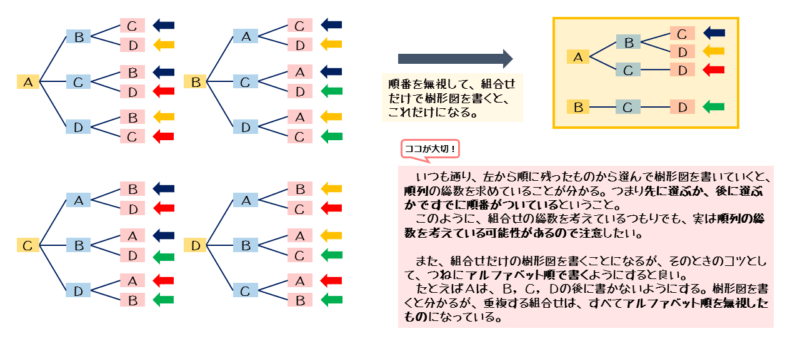
2つ目のコツについて補足しておきます。たとえば、Bが先頭になる樹では、Bよりもアルファベット順が前になるAを右側に書かないようにします。
B,A,CなどのようにAをBよりも右側に書いてしまうと、順序を考慮していることになり、順列になってしまいます。この点に注意して書いていけば、組合せだけを書き出すことができます。
組合せの総数の性質
組合せの総数はCという記号を使って表されますが、その中でもnC0やnCnの値は定義されています。それぞれの意味を考えれば、特に暗記するものではありません。
nC0は、異なるn個から0個を選ぶ組合せの総数のことです。言い換えると、異なるn個から1個も選ばない組合せの総数のことなので、その組合せは1通りしかありません。
また、nCnは、異なるn個からn個を選ぶ組合せの総数のことです。言い換えると、異なるn個から全部を選ぶ組合せの総数のことなので、この組合せも1通りしかありません。
組合せの総数の性質その1
\begin{align*} \quad {}_n \mathrm{ C }_0 &= 1 \\[ 10pt ] {}_n \mathrm{ C }_n &= 1 \end{align*}また、計算では良く使われる性質にnCrの性質があります。
組合せの総数の性質その2
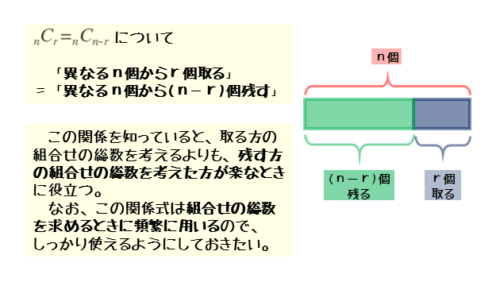
\begin{align*} \quad {}_n \mathrm{ C }_r = {}_n \mathrm{ C }_{n-r} \end{align*}nCrは、異なるn個からr個を選ぶ組合せの総数のことです。異なるn個からr個を選ぶと、n-r個は選ばれずに残ります。
取るものを選べば、結果的に取らない(残す)ものを選ぶことになります。この関係を表したのが先ほどの式(組合せの総数の性質その2)です。
この性質を利用できるようになると、計算がとてもラクになります。入試でも頻繁に利用する性質なので、式の意味を理解しておきましょう。
「異なるn個からr個を選ぶ」は「異なるn個からn-r個を選ばずに残す」と同じ意味。
次は組合せを扱った問題を実際に解いてみましょう。