図形と方程式|2直線の共有点と連立1次方程式の解について

今回は、2直線の共有点と連立1次方程式の解について学習しましょう。2直線の共有点の有無から、連立1次方程式の解のことが分かります。逆に、連立1次方程式の解によって、2直線の関係が分かります。
2直線の共有点と連立1次方程式の解との関係をしっかり理解しましょう。
2直線の共有点と連立1次方程式の解
2直線の共有点と言ってはいますが、正確には「2直線の共有点の座標」です。
2直線の共有点は、両方の直線上にある点です。直線上にある点の座標は直線の方程式の解なので、共有点の座標は、2直線の方程式の解の中でも共通の解となります。
2つの方程式の共通の解とは、連立方程式の解のことです。直線の方程式は1次方程式なので、2直線の方程式を連立すれば、連立1次方程式と言います。
このことから以下のことが言えます。
2直線の共有点と連立1次方程式の解との関係
$2$ 直線
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \quad \cdots \text{①} \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \quad \cdots \text{②} \end{align*}の共有点の座標は、連立 $1$ 次方程式①,②の解として得られる。
よって
$\bullet \ 2$ 直線が $1$ 点で交わる
$\quad \Longleftrightarrow \quad$ 連立方程式①,②はただ $1$ 組の解をもつ
$\bullet \ 2$ 直線が平行で一致しない
$\quad \Longleftrightarrow \quad$ 連立方程式①,②は解をもたない
$\bullet \ 2$ 直線が一致する
$\quad \Longleftrightarrow \quad$ 連立方程式①,②は無数の解をもつ
共有点の座標は、2直線の方程式の解です。このとき、その座標を方程式にそれぞれ代入すると、等式が成り立つことは明らかです。
このような関係があるので、直線上にある点の座標を求めるとき、直線の方程式にx座標やy座標を代入しています。
直線上の点の座標=直線の方程式の解
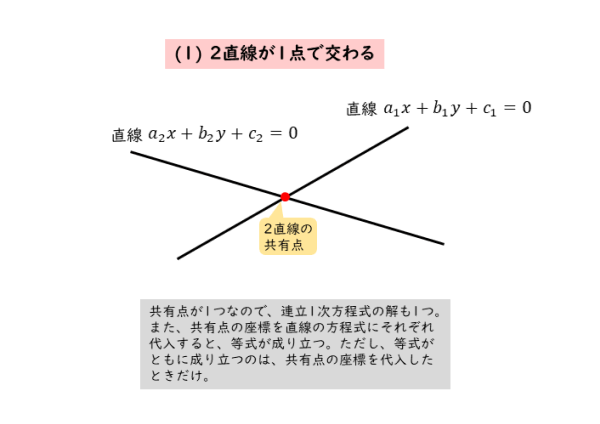
2直線が1点で交わる
2直線が1点で交わるとき、共有点は1つだけです。
このとき、共有点の座標を2直線の方程式に代入すると、等式がともに成り立つ、言い換えると連立1次方程式の解となるのは、共有点の座標の1組だけです。
2直線が1点で交わる=共有点は1つ=連立1次方程式の解は1組
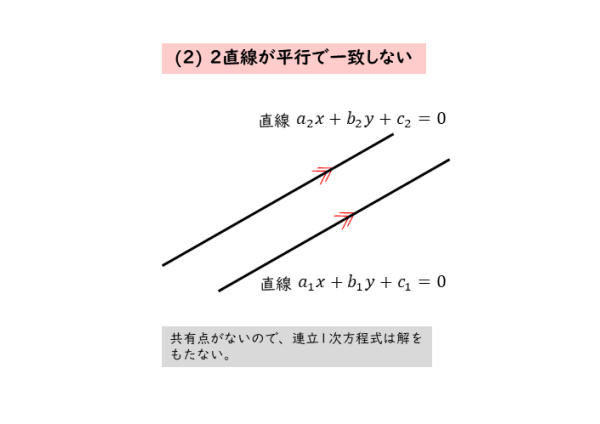
2直線が平行で一致しない
2直線が平行で一致しないとき、共有点はありません。
このとき、2直線の方程式にどんな座標を代入しても、等式がともに成り立つことはありません。つまり、連立1次方程式の解がないということです。
2直線が平行で一致しない=共有点はない=連立1次方程式の解はなし
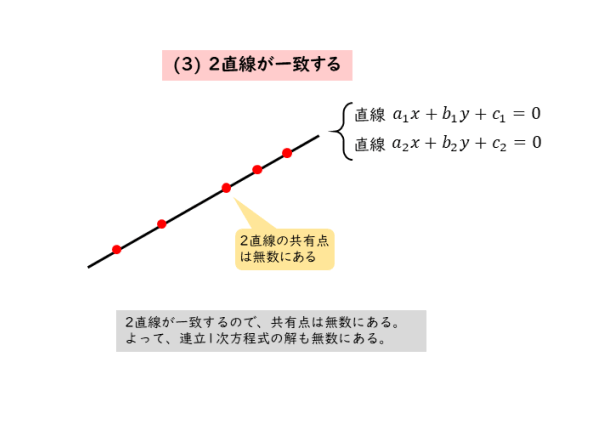
2直線が一致する
2直線が一致するというのは、2直線が重なるということです。
このとき、一方の直線上にある点であれば、必ず他方の直線上にもあります。つまり、すべてが共有点となるわけです。
2直線上にある点はすべて共有点となります。ですから、2直線の方程式に代入して等式がともに成り立つ座標は無数に存在します。つまり、連立1次方程式の解は無数にあります。
2直線が一致する=共有点は直線上の点全体=連立1次方程式の解は無数にある
連立方程式の解が特定の結果を満たすための条件を考えてみよう
次の例題を考えてみましょう。
例題
次の連立方程式
\begin{align*} \quad \left\{ \begin{array}{l} ax+3y-1=0 \\ 3x-2y+c=0 \end{array} \right. \end{align*}の解が、次のようになるための条件を求めよ。
$\quad (1) \quad$ ただ $1$ 組の解をもつ
$\quad (2) \quad$ 解をもたない
$\quad (3) \quad$ 無数の解をもつ
例題(1)の解答・解説
例題(1)
次の連立方程式
\begin{align*} \quad \left\{ \begin{array}{l} ax+3y-1=0 \\ 3x-2y+c=0 \end{array} \right. \end{align*}の解が、次のようになるための条件を求めよ。
$\quad$ ただ $1$ 組の解をもつ
問題では、わざわざ直線の方程式と言及しない場合が多いです。例題のように、連立方程式と言及してあることがあります。2つの方程式を見て、直線の方程式であることに気付くことが大切です。
分かりやすく直線の方程式に変形しましょう。
例題(1)の解答例 1⃣
\begin{align*} \quad \left\{ \begin{array}{l} ax+3y-1=0 \\ 3x-2y+c=0 \end{array} \right. \end{align*}与えられた方程式を変形すると
\begin{align*} &\quad y=-\frac{a}{3}x+\frac{1}{3} \quad \cdots \text{①} \\[ 7pt ] &\quad y=\frac{3}{2}x+\frac{c}{2} \quad \cdots \text{②} \end{align*}①,②式を連立して解いたとき、ただ1組の解をもてば、直線①,②が1点で交わります。
このまま連立方程式を解くと、共有点の座標を求めることができます。ただ、条件を得るのは難しいので、少し工夫します。
2直線が1点で交わるのは、2直線の傾きが一致していないときです。
つまり、2直線が平行でなければ、2直線は1点で交わります。これを踏まえて解答例の続きを記述します。
例題(1)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y=-\frac{a}{3}x+\frac{1}{3} \quad \cdots \text{①} \\[ 7pt ] &\quad y=\frac{3}{2}x+\frac{c}{2} \quad \cdots \text{②} \end{align*}連立方程式①,②がただ $1$ 組の解をもつための条件は、直線①,②が $1$ 点で交わる、すなわち、平行でないことである。
よって
\begin{align*} \quad -\frac{a}{3} \neq \frac{3}{2} \end{align*}すなわち
\begin{align*} \quad a \neq -\frac{9}{2} \end{align*}一般形での2直線の平行条件を利用することもできます。
例題(1)の別解例
\begin{align*} \quad \left\{ \begin{array}{l} ax+3y-1=0 \\ 3x-2y+c=0 \end{array} \right. \end{align*}連立方程式がただ $1$ 組の解をもつための条件は、$2$ 直線の平行条件を満たさないことである。
よって
\begin{align*} \quad a \cdot \left( -2 \right)-3 \cdot 3 \neq 0 \end{align*}これを解くと
\begin{align*} \quad a \neq -\frac{9}{2} \end{align*}なお、一般形から導かれる2直線の平行条件は以下の通りです。
2直線の平行条件
$2$ 直線の方程式を
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}とするとき、$2$ 直線が平行であれば
\begin{align*} \quad a_{1} b_{2}-a_{2} b_{1}=0 \end{align*}が成り立つ。
直線の方程式が一般形で与えられることが多くなります。ですから、この平行条件は意外と重宝します。使いこなせるようにしておきましょう。
例題(2)の解答・解説
例題(2)
次の連立方程式
\begin{align*} \quad \left\{ \begin{array}{l} ax+3y-1=0 \\ 3x-2y+c=0 \end{array} \right. \end{align*}の解が、次のようになるための条件を求めよ。
$\quad$ 解をもたない
例題(1)と同じ要領で解きます。直線の方程式を導くまでは同じなので、「(1)より」などとして省略しても構いません。ここでは記述しておきます。
例題(2)の解答例 1⃣
\begin{align*} \quad \left\{ \begin{array}{l} ax+3y-1=0 \\ 3x-2y+c=0 \end{array} \right. \end{align*}与えられた方程式を変形すると
\begin{align*} &\quad y=-\frac{a}{3}x+\frac{1}{3} \quad \cdots \text{①} \\[ 7pt ] &\quad y=\frac{3}{2}x+\frac{c}{2} \quad \cdots \text{②} \end{align*}連立方程式①,②が解をもたなければ、直線①,②が平行で一致しません。2直線が平行であるための条件は、傾きが一致することです。
ただし、2直線が平行であっても一致するとまずいので、切片も考慮します。これを踏まえて解答例の続きを記述します。
例題(2)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y=-\frac{a}{3}x+\frac{1}{3} \quad \cdots \text{①} \\[ 7pt ] &\quad y=\frac{3}{2}x+\frac{c}{2} \quad \cdots \text{②} \end{align*}連立方程式①,②が解をもたないための条件は、直線①,②が平行で一致しないことである。
よって
\begin{align*} \quad -\frac{a}{3} = \frac{3}{2} \quad \text{かつ} \quad \frac{1}{3} \neq \frac{c}{2} \end{align*}すなわち
\begin{align*} \quad a = -\frac{9}{2} \quad \text{かつ} \quad c \neq \frac{3}{2} \end{align*}したがって
\begin{align*} \quad a = -\frac{9}{2} \ , \ c \neq \frac{3}{2} \end{align*}例題(2)では、一般形による平行条件を利用できますが、2直線が一致しないことも考慮しなければなりません。いずれにしても解答例のように切片の条件が必要になります。
例題(3)の解答・解説
例題(3)
次の連立方程式
\begin{align*} \quad \left\{ \begin{array}{l} ax+3y-1=0 \\ 3x-2y+c=0 \end{array} \right. \end{align*}の解が、次のようになるための条件を求めよ。
$\quad$ 無数の解をもつ
直線の方程式を導くまではこれまでと同様です。
例題(3)の解答例 1⃣
\begin{align*} \quad \left\{ \begin{array}{l} ax+3y-1=0 \\ 3x-2y+c=0 \end{array} \right. \end{align*}与えられた方程式を変形すると
\begin{align*} &\quad y=-\frac{a}{3}x+\frac{1}{3} \quad \cdots \text{①} \\[ 7pt ] &\quad y=\frac{3}{2}x+\frac{c}{2} \quad \cdots \text{②} \end{align*}連立方程式①,②が無数の解をもてば、直線①,②が一致します。2直線が一致するための条件は、傾きと切片の両方が一致することです。
傾きと切片が一致するのは、2直線の方程式が同じ式になるときです。これを踏まえて解答例の続きを記述します。
例題(3)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y=-\frac{a}{3}x+\frac{1}{3} \quad \cdots \text{①} \\[ 7pt ] &\quad y=\frac{3}{2}x+\frac{c}{2} \quad \cdots \text{②} \end{align*}連立方程式①,②が無数の解をもつための条件は、直線①,②が一致することである。
よって
\begin{align*} \quad -\frac{a}{3} = \frac{3}{2} \quad \text{かつ} \quad \frac{1}{3} = \frac{c}{2} \end{align*}すなわち
\begin{align*} \quad a = -\frac{9}{2} \quad \text{かつ} \quad c = \frac{3}{2} \end{align*}したがって
\begin{align*} \quad a = -\frac{9}{2} \ , \ c = \frac{3}{2} \end{align*}ちなみに、一般形での2直線が一致する条件は以下の通りです。この条件を利用して解くこともできます。
2直線が一致するための条件
$2$ 直線の方程式を
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}とするとき、$2$ 直線が一致するための条件は
\begin{align*} \quad \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}} \end{align*}ただし、$a_{2} \neq 0 \ , \ b_{2} \neq 0 \ , \ c_{2} \neq 0$
【導出】
\begin{align*} &\quad y=-\frac{a_{1}}{b_{1}}x-\frac{c_{1}}{b_{1}} \\[ 7pt ] &\quad y=-\frac{a_{2}}{b_{2}}x-\frac{c_{2}}{b_{2}} \end{align*}ただし、$b_{1} \neq 0 \ , \ b_{2} \neq 0$
$2$ 直線が一致するので
\begin{align*} \quad -\frac{a_{1}}{b_{1}}=-\frac{a_{2}}{b_{2}} \ , \ -\frac{c_{1}}{b_{1}}=-\frac{c_{2}}{b_{2}} \end{align*}ここで、$a_{2} \neq 0 \ , \ c_{2} \neq 0$ のとき
\begin{align*} \quad \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \ , \ \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}} \end{align*}したがって
\begin{align*} \quad \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}} \end{align*}ただし、$a_{2} \neq 0 \ , \ b_{2} \neq 0 \ , \ c_{2} \neq 0$
次は、2直線の共有点と連立1次方程式の解を扱った問題を実際に解いてみましょう。