図形と方程式|共点と共線の関係について

今回は、共点と共線の関係について学習しましょう。共点や共線そのものについてはすでに学習済みです。
ここでは共点と共線の間にどんな関係があるかを学習します。
共点・共線
共点や共線という用語についてはすでに見聞きしています。
共点は複数の直線がもつ性質を表す用語です。それに対して、共線は複数の点がもつ性質を表す用語です。名称と内容が逆なので、間違えないようにしましょう。
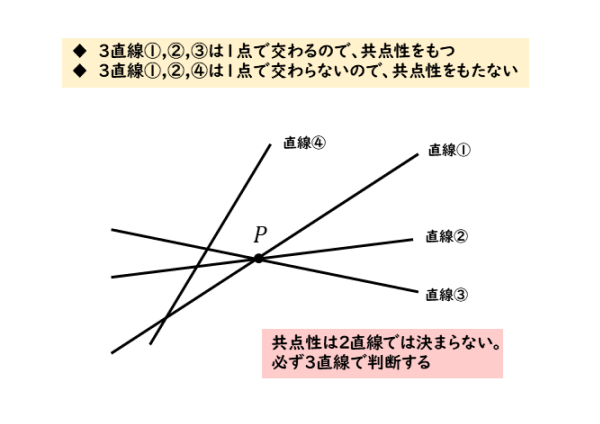
点を共有するという性質のことを共点性と言います。「同一の点を通る3本、または3本以上の直線は共点である」と言います。「共点性をもつ」でも通じます。
「共点」という言葉だけでは勘違いしやすいので、単語だけで覚えないようにしましょう。たとえば「3直線が共点である」という表現で覚えると良いでしょう。
共点である
3直線が1点で交わる=2直線の交点が第3の直線上にある
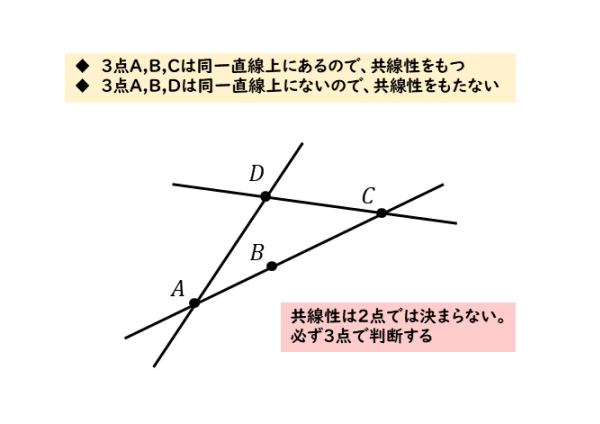
直線を共有するという性質のことを共線性と言います。「同じ直線上にある3つの点、あるいは3点以上の点は共線である」と言います。「共線性をもつ」でも通じます。
こちらも「共線」という言葉だけでは勘違いしやすいので、「3点が共線である」という表現で覚えましょう。
共線である
3点が同じ直線上にある=2点を通る直線上に第3の点がある(=2直線の傾きが一致する)
共点と共線の関係について考えてみよう
次の例題を考えてみましょう。
例題
異なる $3$ 直線
\begin{align*} &\quad x+y=1 \quad \cdots \text{①} \\[ 7pt ] &\quad 4x+5y=1 \quad \cdots \text{②} \\[ 7pt ] &\quad ax+by=1 \quad \cdots \text{③} \end{align*}が $1$ 点で交わるとき、$3$ 点
\begin{align*} \quad (1 \ , \ 1) \ , \ (4 \ , \ 5) \ , \ (a \ , \ b) \end{align*}は同じ直線上にあることを示せ。
例題の解答・解説
3つの直線①,②,③は、1点で交わるので、共点性をもちます。
このとき、3直線の交点の座標を直線の方程式にそれぞれ代入すると、どれも等式が成り立ちます。交点が3直線上にあるということは、その座標が直線の方程式を満たす解であるからです。このことを利用します
例題の解答例 1⃣
\begin{align*} &\quad x+y=1 \quad \cdots \text{①} \\[ 7pt ] &\quad 4x+5y=1 \quad \cdots \text{②} \\[ 7pt ] &\quad ax+by=1 \quad \cdots \text{③} \end{align*}①,②を連立して解くと、①×5-②より
\begin{align*} \quad x=4 \end{align*}これと①より
\begin{align*} \quad y=-3 \end{align*}よって、$2$ 直線①,②の交点の座標は
\begin{align*} \quad (4 \ , \ -3) \end{align*}この交点は直線③上にもあるので
\begin{align*} \quad a \cdot 3+b \cdot \left(-3 \right)=1 \end{align*}よって
\begin{align*} \quad 4a-3b=1 \quad \cdots \text{④} \end{align*}3直線①,②,③の共点性を利用して、定数a,bについての方程式④を導くことができました。
ここでは、定数a,bの値を求める必要がないので、定数a,bについての方程式は1つで問題ありません。
次に、3点が同じ直線上にある、すなわち共線性をもつこと示します。
具体的には、2点を通る直線の方程式に、残りの点の座標を代入すると等式が成り立つことを示します。このとき、先ほど導いた④式を利用します。
例題の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad 4a-3b=1 \quad \cdots \text{④} \end{align*}また、$2$ 点 $(1 \ , \ 1) \ , \ (4 \ , \ 5)$ を通る直線の方程式は
\begin{align*} \quad \left(5-1 \right)\left(x-1 \right)-\left(4-1 \right)\left(y-1 \right)=0 \end{align*}より
\begin{align*} \quad 4\left(x-1 \right)-3\left(y-1 \right)=0 \end{align*}よって
\begin{align*} \quad 4x-3y=1 \end{align*}これに $x=a \ , \ y=b$ を代入すると、④から等式を満たすので、点 $(a \ , \ b)$ は直線 $4x-3y=1$ 上にある。
したがって、$3$ 点 $(1 \ , \ 1) \ , \ (4 \ , \ 5) \ , \ (a \ , \ b)$ は、同じ直線 $4x-3y=1$ 上にある。
何だか不思議な感じがしますが、難しく考える必要はありません。共点性から得られた④式を、共線性を示すために利用しただけです。
例題の別解例
一般に次のような性質が成り立つので、この性質を利用して解くこともできます。
共点と共線の関係
点 $(p \ , \ q)$ が直線 $ax+by+c=0$ 上にある
\begin{align*} \Longleftrightarrow \quad ap+bq+c=0 \end{align*}$\Longleftrightarrow \quad$ 点 $(a \ , \ b)$ が直線 $px+qy+c=0$ 上にある
この性質を理解するには、座標代入後の式をどう捉えているかがポイントになります。
共点と共線の関係
点 $(p \ , \ q)$ が直線 $ax+by+c=0$ 上にあるとき
\begin{align*} \quad a \cdot p+b \cdot q+c=0 \end{align*}すなわち
\begin{align*} \quad ap+bq+c=0 \end{align*}また、点 $(a \ , \ b)$ が直線 $px+qy+c=0$ 上にあるとき
\begin{align*} \quad p \cdot a+q \cdot b+c=0 \end{align*}すなわち
\begin{align*} \quad ap+bq+c=0 \end{align*}どちらも同じ等式が得られる。
座標や直線の方程式は異なりますが、座標を代入した後の等式は同じです。ですから、座標代入後の等式から見れば、どちらにも解釈できるわけです。
このような性質は、共線性をもつ点や、共点性をもつ直線があるから成り立ちます。
この性質を利用すると、以下のような解答例になります。
例題の別解例
\begin{align*} &\quad x+y=1 \quad \cdots \text{①} \\[ 7pt ] &\quad 4x+5y=1 \quad \cdots \text{②} \\[ 7pt ] &\quad ax+by=1 \quad \cdots \text{③} \end{align*}原点を通らない $3$ 直線①,②,③が $1$ 点で交わるので、その点の座標を $P(p \ , \ q)$ とすると、$P$ は原点にはならない。
$3$ 直線①,②,③が点 $P$ を通ることから
\begin{align*} \quad p+q=1 \ , \ 4p+5q=1 \ , \ ap+bq=1 \end{align*}すなわち
\begin{align*} &\quad p \cdot 1+q \cdot 1=1 \quad \cdots \text{⑤} \\[ 7pt ] &\quad p \cdot 4+q \cdot 5=1 \quad \cdots \text{⑥} \\[ 7pt ] &\quad p \cdot a+q \cdot b=1 \quad \cdots \text{⑦} \end{align*}であり、$p \neq 0$ または $q \neq 0$
ここで、直線の方程式 $px+qy=1$ を考えると、⑤~⑦から、$3$ 点 $(1 \ , \ 1) \ , \ (4 \ , \ 5) \ , \ (a \ , \ b)$ は直線 $px+qy=1$ 上にある。
座標を代入した後の等式の捉え方を変えたのが、⑤~⑦式です。
交点の座標を3直線の方程式にそれぞれ代入した後の等式から、3点の座標を同一直線の方程式に代入した後の等式へと解釈しなおしています。
次は、共点と共線の関係を扱った問題を実際に解いてみましょう。