図形と方程式|座標を利用した証明(垂心)について

座標を利用した証明(垂心)を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
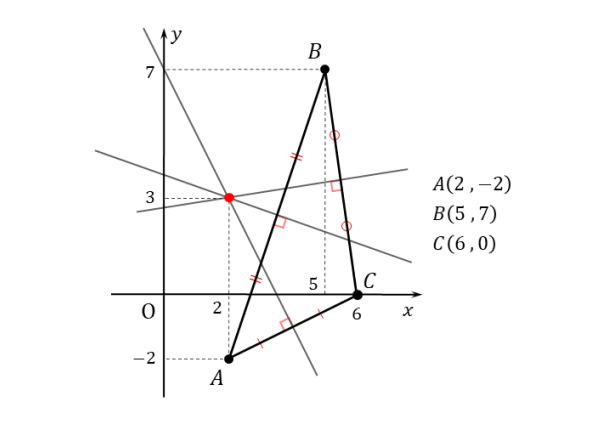
$xy$ 平面上に $3$ 点 $A(2 \ , \ -2) \ , \ B(5 \ , \ 7) \ , \ C(6 \ , \ 0)$ がある。$\triangle {ABC}$ の各辺の垂直二等分線は $1$ 点で交わることを証明せよ。
問の解答・解説
問のように、各辺の垂直二等分線は1点で交わります。この点のことを外心と言います。問は、外心ができることの証明です。
問題文を読みながら作図してみましょう。単なる垂線ではなく、各辺の中点を通る垂直二等分線を作図しなければなりません。
垂心のときと基本的な流れは変わりませんが、垂直二等分線の方程式なので、傾きだけでなく、中点の座標も必要になります。まず、直線ACの垂直二等分線を求めます。
問の解答例 1⃣
線分 $AC$ の中点の座標は
\begin{align*} \quad \left(\frac{2+6}{2} \ , \ \frac{-2+0}{2} \right) \end{align*}すなわち
\begin{align*} \quad (4 \ , \ -1) \end{align*}直線 $AC$ の傾きは
\begin{align*} \quad \frac{0-(-2)}{6-2}=\frac{1}{2} \end{align*}よって、直線 $AC$ の垂直二等分線は点 $(4 \ , \ -1)$ を通り、その傾きは $-2$ である。
したがって、直線 $AC$ の垂直二等分線の方程式は
\begin{align*} \quad y-\left(-1 \right)=-2 \left(x-4 \right) \end{align*}すなわち
\begin{align*} \quad y=-2x+7 \quad \cdots \text{①} \end{align*}次に、直線ABの垂直二等分線を求めます。
問の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y=-2x+7 \quad \cdots \text{①} \end{align*}線分 $AB$ の中点の座標は
\begin{align*} \quad \left(\frac{2+5}{2} \ , \ \frac{-2+7}{2} \right) \end{align*}すなわち
\begin{align*} \quad \left(\frac{7}{2} \ , \ \frac{5}{2} \right) \end{align*}直線 $AB$ の傾きは
\begin{align*} \quad \frac{7-(-2)}{5-2}=3 \end{align*}よって、直線 $AB$ の垂直二等分線は点
\begin{align*} \quad \left(\frac{7}{2} \ , \ \frac{5}{2} \right) \end{align*}を通り、その傾きは
\begin{align*} \quad -\frac{1}{3} \end{align*}である。
したがって、直線 $AB$ の垂直二等分線の方程式は
\begin{align*} \quad y-\left(\frac{5}{2} \right)=-\frac{1}{3} \left(x-\frac{7}{2} \right) \end{align*}すなわち
\begin{align*} \quad x+3y-11=0 \quad \cdots \text{②} \end{align*}直線ABの垂直二等分線の方程式(②式)が一般形となっているのは、傾きや切片が分数となるからです。
①,②式の連立方程式を解くとき、加減法ではなく、代入法で解けるので、①式に合わせなくても問題ありません。
直線ACの垂直二等分線と直線ABの垂直二等分線との交点の座標を求めます。①,②式を連立して解きます。
問の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad y=-2x+7 \quad \cdots \text{①} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad x+3y-11=0 \quad \cdots \text{②} \end{align*}方程式①,②を連立させて解く。
①を②に代入して
\begin{align*} \quad x+3 \left(-2x+7 \right)-11=0 \end{align*}より
\begin{align*} \quad x=2 \end{align*}また
\begin{align*} \quad y=3 \end{align*}したがって、$2$ 直線①,②の交点の座標は
\begin{align*} \quad (2 \ , \ 3) \end{align*}さいごに、線分BCの垂直二等分線の方程式を求め、この直線上に点(2,3)があるか確認します。
問の解答例 4⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad (2 \ , \ 3) \end{align*}線分 $BC$ の中点の座標は
\begin{align*} \quad \left(\frac{5+6}{2} \ , \ \frac{7+0}{2} \right) \end{align*}すなわち
\begin{align*} \quad \left(\frac{11}{2} \ , \ \frac{7}{2} \right) \end{align*}直線 $BC$ の傾きは
\begin{align*} \quad \frac{0-7}{6-5}=-7 \end{align*}よって、直線 $BC$ の垂直二等分線は点
\begin{align*} \quad \left(\frac{11}{2} \ , \ \frac{7}{2} \right) \end{align*}を通り、その傾きは
\begin{align*} \quad \frac{1}{7} \end{align*}である。
したがって、直線 $BC$ の垂直二等分線の方程式は
\begin{align*} \quad y-\left(\frac{7}{2} \right)=\frac{1}{7} \left(x-\frac{11}{2} \right) \end{align*}すなわち
\begin{align*} \quad x-7y+19=0 \quad \cdots \text{③} \end{align*}直線BCの垂直二等分線の方程式も分数を嫌って一般形で表しています。
先ほど得られた2直線①,②の交点の座標を代入して、方程式③の解であることを確かめます。直線の方程式を満たす解は、直線上にある点の座標です。
問の解答例 5⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad x-7y+19=0 \quad \cdots \text{③} \end{align*}③の左辺に $x=2 \ , \ y=3$ を代入すると
\begin{align*} \quad 2-7 \cdot 3+19=2-21+19=0 \end{align*}となり、$x=2 \ , \ y=3$ は③を満たすので、点 $(2 \ , \ 3)$ は直線③上にある。
したがって、$\triangle {ABC}$ の各辺の垂直二等分線は $1$ 点 $(2 \ , \ 3)$ で交わる。
証明するために、2直線の垂直条件や中点の座標など、すでに学習した事項を適切に利用しなければなりません。忘れた事柄がないか確認しながら進めていきましょう。
3直線が交わることの証明
2直線の交点の座標を求めて、残りの直線上にあることを示すのが一般的。
Recommended books
先日、英語の民間検定試験導入に変更があった大学共通テスト。今後も内容が変更される可能性があるので、こまめに情報収集しておきたいところです。
数学でも記述問題が導入されますが、センター試験と本質的には変わりません。共通テストであっても誘導形式に沿って解くので、大筋ではほとんど変わりません。
また、数学ではどんな問題でも基本的に過程を無視して解くことはできません。つまり、記述しながら解くことは、共通テストに限らず、日常的に行います。日常学習で意識的に取り組んでいれば、記述の訓練は特別に必要ありません。
ただ、共通テストの傾向は知っておいて損はありません。傾向を知り、それに合わせて準備する。このことは時間を掛ければ掛けるほど効果的です。ここでは、傾向と対策のための教材を紹介します。
オススメ 『大学入学共通テスト 数学予想問題集』シリーズ
共通テストにおける数学の傾向は、これまでに実施されたプレテストを分析することで掴むことができます。あくまでも傾向なので、確実に当たるわけではありません。しかし、出題者の意図からどのような問題が出題されそうかは、対策する上でとても役立ちます。
日常学習でも「記述問題に出題されそうだ」などと自分なりに考えながら取り組むことが大切です。
問題の解説だけでなく、問題の背景にある考え方まで説明してくれる対策書として大好評を博した「共通テスト予想問題集」シリーズを、2021年1月に実施された試験の出題にもとづいて全面改訂。
「読解問題」とでも言うべき共通テストの特殊な形式に完全対応。本冊の前付部分では、出題傾向の分析だけでなく、各単元の具体的な勉強法まで提示。「理想の共通テスト演習書」がさらにパワーアップ。
公式サイトでは、一部の内容を閲覧できます。
KADOKAWAの公式サイト
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごにもう一度まとめ
- 垂心や外心の証明では、2直線の垂直条件から傾きを求めよう。
- 外心の証明では、線分の中点の座標を求めよう。
- 直線の方程式を求めるときには、傾きと1点の座標を用いることが多い。
- 直線の方程式を表すとき、係数によっては一般形を利用しよう。
- 3直線が1点で交わることの証明では、2直線の交点が残りの直線上にあることを示そう。