数学2
今回は、座標を利用した証明について学習しましょう。辺の長さの関係を表す等式が成り立つことを証明する際に、辺の長さを求めるのではなく、座標を用います。
座標を用いることで証明しやすくなるのですが、上手に座標平面に図形を設置できなければ、かえって難しくなります。そうならないように、ポイントをしっかり押さえましょう。
座標を利用した証明
上述したように、座標を利用すると図形の性質を簡単に証明できる場合があります。ここで注意したいのは2つです。
座標を用いた証明での注意点
- 座標軸をどこにとるか
- 与えられた図形を座標を用いてどう表すか
この2点を疎かにすると、計算が大変になり、かえって難しい証明になってしまいます。後の計算が楽になるように、座標軸を定める必要があります。
座標軸の定め方は1つではありませんが、次の2点を意識しましょう。
座標軸を定めるときのコツ
- 頂点や特定の点の座標に0が多く含まれるようにする。
- 座標を定義するとき、できるだけ変数が少なくなるようにする。
座標に0が多く含まれるには、問題で扱う点がx軸やy軸上になるべく多く配置されるようにします。計算量が減るので、辺の長さを求めるのが易しくなります。
また、変数を少なくするには、図形の対称性を利用します。たとえば、原点やx,y軸に対称になるように点をとります。変数が少なくなれば、必要な方程式の数を減らすことができます。
ほとんどの問題では、未知のものに対応させて変数を当てますが、そうすると変数が多くなります。ですから、変数をなるべく少なくするという考え方はとても大切です。
以上のことから分かるのは、証明する前の準備で難易度が決まるということです。できるだけ難易度を下げるために、しっかり考えた上で座標を設定しましょう。そうは言っても、設定の仕方はほとんど変わらないので、例題を真似てみるのが良いでしょう。
座標を利用して証明してみよう
例題
\begin{align*}
&\text{$\triangle {ABC}$ の重心を $G$ とするとき、} \\[ 5pt ]
&\quad AB^{\scriptsize{2}}+BC^{\scriptsize{2}}+CA^{\scriptsize{2}}=3 \left( GA^{\scriptsize{2}}+GB^{\scriptsize{2}}+GC^{\scriptsize{2}} \right) \\[ 7pt ]
&\text{が成り立つことを証明せよ。}
\end{align*}
例題の解答・解説
図形を座標平面上にいきなり設置するのは、慣れていないと意外と難しいです。まずは図形だけを作図してみて、どのような点が出てくるのかを確認しましょう。問題で出てくる点以外にも必要な点があることに気付くはずです。
重心をとるには、頂点とその対辺の中点とを結ぶ中線が必要です。対辺の中点は問題で与えられていません。中点も考慮して図形の配置を考えましょう。
まず、座標軸を定めます。
例題の解答例 1⃣
\begin{align*}
&\text{直線 $BC$ を $x$ 軸に、辺 $BC$ の垂直二等分線を $y$ 軸に} \\[ 5pt ]
&\text{とると、線分 $BC$ の中点は原点 $O$ になる。}
\end{align*}
座標軸が定まったら、点の座標を定義します。変数がなるべく少なくなるようにします。
例題の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\text{とると、線分 $BC$ の中点は原点 $O$ になる。} \\[ 5pt ]
&\text{$3$ 点 $A \ , \ B \ , \ C$ の座標を} \\[ 5pt ]
&\quad A \ (3a \ , \ 3b) \ , \ B \ (-c \ , \ 0) \ , \ C \ (c \ , \ 0) \\[ 7pt ]
&\text{とすると、点 $G$ は重心であるので} \\[ 5pt ]
&\quad G \ (a \ , \ b) \\[ 7pt ]
&\text{と表すことができる。}
\end{align*}
頂点B,Cの座標は原点(またはy軸)に関して対称なので、同じ変数を利用できます。また、頂点Aの座標については、重心Gの座標を考慮に入れます。
線分AOは重心Gによって2:1に内分されます。頂点B,Cの座標がすでに定義されているので、重心Gの座標に分数が含まれないように、頂点Aの座標を設定します。
作図すると以下の通りです。
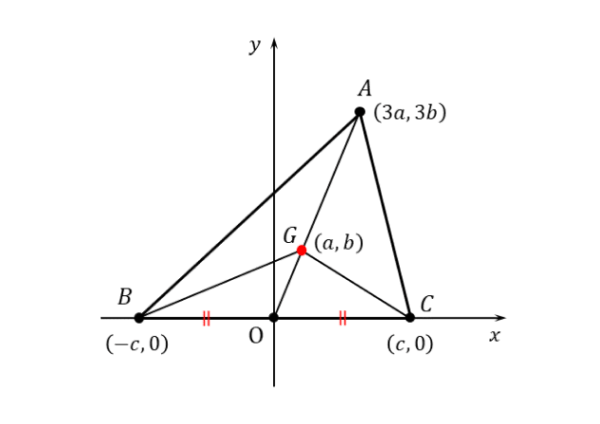 座標軸と点の座標の設定
座標軸と点の座標の設定 ほとんどの問題では、底辺がx軸と重なるように三角形を設置すると上手くいきます。また、答案を作成するのは、先に作図を済ませてからにしましょう。
座標軸や座標が定まったので、等式が成り立つことを証明します。左辺の計算です。
例題の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad A \ (3a \ , \ 3b) \ , \ B \ (-c \ , \ 0) \ , \ C \ (c \ , \ 0) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad G \ (a \ , \ b) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\text{このとき} \\[ 5pt ]
&\quad AB^{\scriptsize{2}}+BC^{\scriptsize{2}}+CA^{\scriptsize{2}} \\[ 7pt ]
&\quad =\left\{ \left(-c-3a \right)^{\scriptsize{2}}+\left(0-3b \right)^{\scriptsize{2}} \right\}+\left\{ c-\left(-c \right) \right\}^{\scriptsize{2}}+\left\{ \left(3a-c \right)^{\scriptsize{2}}+\left(3b-0 \right)^{\scriptsize{2}} \right\} \\[ 7pt ]
&\quad =\left\{ \left(c+3a \right)^{\scriptsize{2}}+\left(3b \right)^{\scriptsize{2}} \right\}+\left(2c \right)^{\scriptsize{2}}+\left\{ \left(3a-c \right)^{\scriptsize{2}}+\left(3b \right)^{\scriptsize{2}} \right\} \\[ 7pt ]
&\quad =\left(c^{\scriptsize{2}}+6ca+9a^{\scriptsize{2}}+9b^{\scriptsize{2}} \right)+4c^{\scriptsize{2}}+\left(9a^{\scriptsize{2}}-6ca+c^{\scriptsize{2}}+9b^{\scriptsize{2}} \right) \\[ 7pt ]
&\quad =18a^{\scriptsize{2}}+18b^{\scriptsize{2}}+6c^{\scriptsize{2}} \\[ 7pt ]
&\quad =3 \left(6a^{\scriptsize{2}}+6b^{\scriptsize{2}}+2c^{\scriptsize{2}} \right) \quad \cdots \text{①}
\end{align*}
辺BCはx軸上にある2点間の距離です。ですから、三平方の定理を利用しなくても、x座標だけで計算できます。他の辺の長さの求め方とは異なるので注意しましょう。
次に、右辺を計算します。
例題の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad A \ (3a \ , \ 3b) \ , \ B \ (-c \ , \ 0) \ , \ C \ (c \ , \ 0) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad G \ (a \ , \ b) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad =3 \left(6a^{\scriptsize{2}}+6b^{\scriptsize{2}}+2c^{\scriptsize{2}} \right) \quad \cdots \text{①} \\[ 7pt ]
&\text{また} \\[ 5pt ]
&\quad GA^{\scriptsize{2}}+GB^{\scriptsize{2}}+GC^{\scriptsize{2}} \\[ 7pt ]
&\quad =\left\{ \left(3a-a \right)^{\scriptsize{2}}+\left(3b-b \right)^{\scriptsize{2}} \right\}+\left\{ \left(-c-a \right)^{\scriptsize{2}}+\left(0-b \right)^{\scriptsize{2}} \right\}+\left\{ \left(c-a \right)^{\scriptsize{2}}+\left(0-b \right)^{\scriptsize{2}} \right\} \\[ 7pt ]
&\quad =\left\{ \left(2a \right)^{\scriptsize{2}}+\left(2b \right)^{\scriptsize{2}} \right\}+\left\{ \left(c+a \right)^{\scriptsize{2}}+b^{\scriptsize{2}} \right\}+\left\{ \left(c-a \right)^{\scriptsize{2}}+b^{\scriptsize{2}} \right\} \\[ 7pt ]
&\quad =\left(4a^{\scriptsize{2}}+4b^{\scriptsize{2}} \right)+\left(c^{\scriptsize{2}}+2ca+a^{\scriptsize{2}}+b^{\scriptsize{2}} \right)+\left(c^{\scriptsize{2}}-2ca+a^{\scriptsize{2}}+b^{\scriptsize{2}} \right) \\[ 7pt ]
&\quad =6a^{\scriptsize{2}}+6b^{\scriptsize{2}}+2c^{\scriptsize{2}} \quad \cdots \text{②}
\end{align*}
右辺全体の計算ではなく、必要な部分だけを計算しておきましょう。
与式を導くには、②式を①式に代入します。これで等式が成り立つことを示せます。
例題の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad =3 \left(6a^{\scriptsize{2}}+6b^{\scriptsize{2}}+2c^{\scriptsize{2}} \right) \quad \cdots \text{①} \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad =6a^{\scriptsize{2}}+6b^{\scriptsize{2}}+2c^{\scriptsize{2}} \quad \cdots \text{②} \\[ 7pt ]
&\text{①,②より} \\[ 5pt ]
&\quad AB^{\scriptsize{2}}+BC^{\scriptsize{2}}+CA^{\scriptsize{2}}=3 \left( GA^{\scriptsize{2}}+GB^{\scriptsize{2}}+GC^{\scriptsize{2}} \right)
\end{align*}
このように座標を用いて等式を証明することができます。また、座標軸や点の座標を上手に定めると、2点間の距離を求める計算が易しくなります。
次は、座標を利用した証明を扱った問題を実際に解いてみましょう。











