データの分析｜データの相関関係について

07/11/2021数学１

共分散や相関係数などを扱った問題を解いてみよう

次の問題を解いてみましょう。

問１

下の表は、$10$ 人の生徒に $50$ 点満点の $2$ 種類のテスト $A \ , \ B$ を行った得点の結果である。テスト $A \ , \ B$ の得点をそれぞれ $x \ , \ y$ とするとき、 $x$ と $y$ の相関係数 $r$ を求めよ。ただし、小数第 $3$ 位を四捨五入せよ。

\begin{align*} \begin{array}{c|c|c|c|c|c|c|c|c|c|c} \scriptsize{\text{生徒の番号}} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\[ 5pt ] \hline x & 43 & 41 & 43 & 38 & 39 & 42 & 42 & 39 & 41 & 42 \\[ 5pt ] \hline y & 49 & 42 & 44 & 36 & 40 & 44 & 45 & 42 & 42 & 46 \end{array} \end{align*}

問１の解答・解説

問１は、２つの変量の相関係数を求める問題です。公式を用いて相関係数を求めますが、できるだけ手際よく計算するために、表を活用します。

問１の解答例 1⃣

\begin{align*} \begin{array}{c|c|c} \scriptsize{\text{番号}} & x & y \\[ 5pt ] \hline 1 & 43 & 49 \\[ 5pt ] \hline 2 & 41 & 42 \\[ 5pt ] \hline 3 & 43 & 44 \\[ 5pt ] \hline 4 & 38 & 36 \\[ 5pt ] \hline 5 & 39 & 40 \\[ 5pt ] \hline 6 & 42 & 44 \\[ 5pt ] \hline 7 & 42 & 45 \\[ 5pt ] \hline 8 & 39 & 42 \\[ 5pt ] \hline 9 & 41 & 42 \\[ 5pt ] \hline 10 & 42 & 46 \\[ 5pt ] \hline \scriptsize{\text{計}} & 410 & 430 \end{array} \end{align*}

表の計の欄を利用して、２つの変量ｘ，ｙの平均値 $\overline{x} \ , \ \overline{y}$ をそれぞれ求めます。

問１の解答例 2⃣

\begin{align*} \quad \vdots \end{align*}

$x \ , \ y$ の平均値を $\overline{x} \ , \ \overline{y}$ とする。

\begin{align*} &\text{表より} \\[ 5pt ] &\quad \overline{x} = \frac{410}{10} = 41 \\[ 7pt ] &\quad \overline{y} = \frac{430}{10} = 43 \end{align*}

平均値が分かったので、偏差、偏差の２乗、偏差の積を表にまとめます。

問１の解答例 3⃣

\begin{align*} \begin{array}{c|c|c|c|c|c|c|c} \scriptsize{\text{番号}} & x & y & x- \overline{x} & y- \overline{y} & (x- \overline{x})^{\tiny{2}} & (y- \overline{y})^{\tiny{2}} & (x- \overline{x})(y- \overline{y}) \\[ 5pt ] \hline 1 & 43 & 49 & 2 & 6 & 4 & 36 & 12 \\[ 5pt ] \hline 2 & 41 & 42 & 0 & -1 & 0 & 1 & 0 \\[ 5pt ] \hline 3 & 43 & 44 & 2 & 1 & 4 & 1 & 2 \\[ 5pt ] \hline 4 & 38 & 36 & -3 & -7 & 9 & 49 & 21 \\[ 5pt ] \hline 5 & 39 & 40 & -2 & -3 & 4 & 9 & 6 \\[ 5pt ] \hline 6 & 42 & 44 & 1 & 1 & 1 & 1 & 1 \\[ 5pt ] \hline 7 & 42 & 45 & 1 & 2 & 1 & 4 & 2 \\[ 5pt ] \hline 8 & 39 & 42 & -2 & -1 & 4 & 1 & 2 \\[ 5pt ] \hline 9 & 41 & 42 & 0 & -1 & 0 & 1 & 0 \\[ 5pt ] \hline 10 & 42 & 46 & 1 & 3 & 1 & 9 & 3 \\[ 5pt ] \hline \scriptsize{\text{計}} & 410 & 430 & 0 & 0 & 28 & 112 & 49 \end{array} \end{align*}

２つの変量ｘ，ｙでそれぞれ偏差や偏差の２乗などを求めるので、かなり煩雑になります。ミスが増えるので注意深く取り組みましょう。

表の計の欄を利用して、相関係数を求めます。

問１の解答例 4⃣

表より、相関係数 $r$ を求めると

\begin{align*} \quad r &= \frac{49}{\sqrt{28 \cdot 112}} \\[ 10pt ] &= \frac{49}{\sqrt{ 2^{\scriptsize{2}} \cdot 7 \cdot 4^{\scriptsize{2}} \cdot 7 }} \\[ 10pt ] &= \frac{49}{2 \cdot 4 \cdot 7} \\[ 10pt ] &\fallingdotseq 0.88 \end{align*}

相関係数の計算では、共分散と標準偏差ではなく、変形後の式（３行目の式）を利用しています。

表を利用するときの相関係数

\begin{align*} \quad r &= \frac{s_{\scriptsize{xy}}}{s_{\scriptsize{x}} \ s_{\scriptsize{y}}} \\[ 10pt ] &= \frac{(x_{\scriptsize{1}} \ – \overline{x} ) (y_{\scriptsize{1}} \ – \overline{y} ) + (x_{\scriptsize{2}} \ – \overline{x} ) (y_{\scriptsize{2}} \ – \overline{y} ) + \cdots + (x_{\scriptsize{n}} \ – \overline{x} ) (y_{\scriptsize{n}} \ – \overline{y} )}{\sqrt{ \left\{ (x_{\scriptsize{1}} \ – \overline{x} )^{\scriptsize{2}} + (x_{\scriptsize{2}} \ – \overline{x} )^{\scriptsize{2}} + \cdots + (x_{\scriptsize{n}} \ – \overline{x} )^{\scriptsize{2}} \right\} \left\{ (y_{\scriptsize{1}} \ – \overline{y} )^{\scriptsize{2}} + (y_{\scriptsize{2}} \ – \overline{y} )^{\scriptsize{2}} + \cdots + (y_{\scriptsize{n}} \ – \overline{y} )^{\scriptsize{2}} \right\} }} \\[ 10pt ] &= \frac{(x \ – \overline{x} ) (y \ – \overline{y} ) \ {\scriptsize{\text{の和}}} }{\sqrt{ \left\{ (x_ \ – \overline{x} )^{\scriptsize{2}} \ {\scriptsize{\text{の和}}} \right\} \left\{ (y \ – \overline{y} )^{\scriptsize{2}} \ {\scriptsize{\text{の和}}} \right\} }} \end{align*}

相関係数を求める計算は煩雑になりやすいので、表を上手に利用して計算しましょう。

次の問題を解いてみましょう。

問２

下の表は、$2$ つの変量 $x \ , \ y$ のデータである。

$(1)$ これらのデータについて、$0.72 \ , \ -0.19 \ , \ -0.85$ のうち、$x$ と $y$ との相関係数に最も近いものはどれか。

$(2)$ 表の右端のデータの $y$ の値を $68$ に変更すると、$x$ と $y$ の相関係数の絶対値は大きくなるか、それとも小さくなるか。

\begin{align*} \begin{array}{c|c|c|c|c|c|c} x & 80 & 70 & 62 & 72 & 90 & 78 \\[ 5pt ] \hline y & 58 & 72 & 83 & 71 & 52 & 78 \end{array} \end{align*}

問２は、相関係数を求める問題と、データの修正の前後の相関係数を比較する問題です。

問２(1)の解答・解説

問２(1)

下の表は、$2$ つの変量 $x \ , \ y$ のデータである。

これらのデータについて、$0.72 \ , \ -0.19 \ , \ -0.85$ のうち、$x$ と $y$ との相関係数に最も近いものはどれか。

\begin{align*} \begin{array}{c|c|c|c|c|c|c} x & 80 & 70 & 62 & 72 & 90 & 78 \\[ 5pt ] \hline y & 58 & 72 & 83 & 71 & 52 & 78 \end{array} \end{align*}

問２(1)の相関係数を求めるために、修正前のデータを表にまとめます。

問２(1)の解答例 1⃣

\begin{align*} \begin{array}{c|c|c} & x & y \\[ 5pt ] \hline 1 & 80 & 58 \\[ 5pt ] \hline 2 & 70 & 72 \\[ 5pt ] \hline 3 & 62 & 83 \\[ 5pt ] \hline 4 & 72 & 71 \\[ 5pt ] \hline 5 & 90 & 52 \\[ 5pt ] \hline 6 & 78 & 78 \\[ 5pt ] \hline \scriptsize{\text{計}} & 452 & 414 \end{array} \end{align*}

表の計の欄を利用して、２つの変量ｘ，ｙの平均値 $\overline{x} \ , \ \overline{y}$ をそれぞれ求めます。

問２(1)の解答例 2⃣

\begin{align*} \quad \vdots \\[ 7pt ] \end{align*}

$x \ , \ y$ の平均値を $\overline{x} \ , \ \overline{y}$ とする。

\begin{align*} &\text{表より} \\[ 5pt ] &\quad \overline{x} = \frac{452}{6} = \frac{226}{3} \\[ 7pt ] &\quad \overline{y} = \frac{414}{6} = 69 \end{align*}

ここで気付いたと思いますが、変量ｘの平均値は、割り切れずに分数になりました。このままだと、ｘの偏差を求めるのがとても大変です。

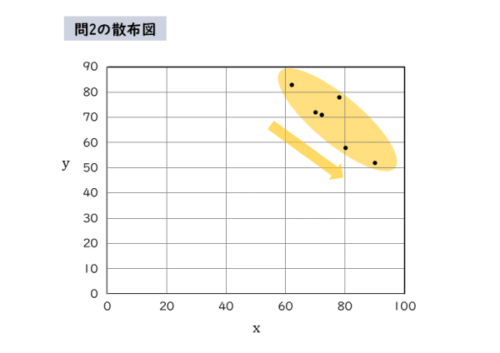
このようなときは散布図を実際に書いてみましょう。値の数はそれほど多くないので難しくありません。散布図は以下のようになります。

散布図から負の相関関係があることが分かります。あとはその値ですが、散布図において、点の配列にできるだけ合うように引いた直線を考えます。

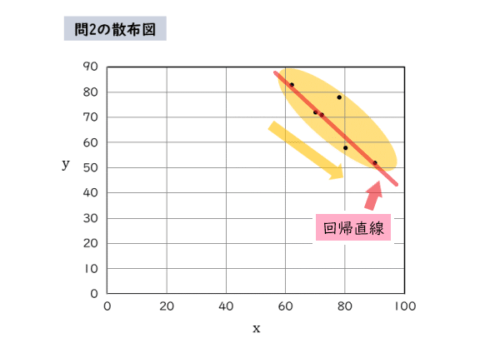
点の配列に合わせて引いた直線を回帰直線と言います。点がこの直線の上やその近くに分布していればいるほど、相関関係が強い、つまり相関係数が１または－１に近い値となります。

問２(1)の解答例 3⃣

\begin{align*} \quad \vdots \end{align*}

$x \ , \ y$ のデータを散布図に表す。

散布図より、点が右下がりの直線の上やその近くに分布している

よって、負の相関が強いので、相関係数は $-0.85$ と考えられる。

相関係数が問題文の中で与えられている場合、計算するのが面倒な場合があります。そのような場合は散布図を書いてみて、点の分布を視覚化してみましょう。

相関係数がすでに与えられている場合、散布図を書いて考えよう。

問２(2)の解答・解説

問２(2)

下の表は、$2$ つの変量 $x \ , \ y$ のデータである。

表の右端のデータの $y$ の値を $68$ に変更すると、$x$ と $y$ の相関係数の絶対値は大きくなるか、それとも小さくなるか。

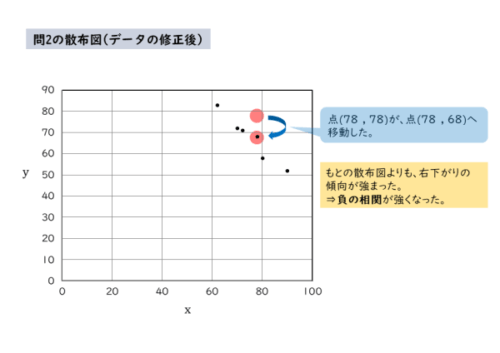
\begin{align*} \begin{array}{c|c|c|c|c|c|c} x & 80 & 70 & 62 & 72 & 90 & 78 \\[ 5pt ] \hline y & 58 & 72 & 83 & 71 & 52 & 78 \end{array} \end{align*}

問２(2)は、データに変更があったとき、相関係数がどのように変化するかを考える問題です。修正の前後で移動する点に注目します。

データが変更された点が移動すると、点の分布がより直線的になりました。変更前よりも負の相関が強くなったことが分かります。

問２(2)の解答例

散布図より、変更後の点の分布は変更前に比べてより直線的になっている。

よって、負の相関が強くなり、相関係数はより $-1$ に近づいたと考えられる。

したがって、相関係数の絶対値は大きくなる。

問２は、入試でも出題されそうな問題です。データの変更によって、相関係数や散布図がどのように変化するのかをしっかり把握することが大切です。

データに変更があったとき、変更箇所に注目しよう。

Recommended books

データの分析を扱った問題は、測定値や観測値が多いと手際よく表やグラフを使って整理していく必要があります。また、表やグラフの目の付け所も知っておかなければなりません。こればかりは頭で分かっていても、実際に整理したり、表やグラフを扱ったりしたことがないと手際よくできません。

ただ、データを手早く扱うコツや表やグラフから読み取るコツを掴んでしまえば、得点源にできる単元です。単元別の問題集で集中的に取り組んでマスターしましょう。

これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。

オススメその１『教科書だけでは足りない大学入試攻略 7日間完成データの分析』

『教科書だけでは足りない大学入試攻略 7日間完成データの分析』は、「データの分析」の学習を短期間でこなすための教材です。１日60分の学習を７日間で完成させることができます。短期間で周回できます。また、教科書レベルから扱っているので、基礎から習得できます。

内容をできる限り絞り、短時間で「データの分析」の学習が一通りできるようにしました。また、微妙な違いがわかることが必要な「図の読み取り」については、多くの図を掲載し、違いが判断できるようにしました。「計算方法」については、効率よく計算を行うことを最優先に、その計算方法を徹底的にマスターできるようにしました。

教科書だけでは足りない大学入試攻略7日間完成データの分析

created by Rinker

オススメその２『改訂版佐々木隆宏の数学I「データの分析」が面白いほどわかる本』

『改訂版佐々木隆宏の数学I「データの分析」が面白いほどわかる本』は、参考書兼問題集です。教科書よりも丁寧に解説されているので、教科書で躓いてもこれでカバーできます。算数から扱っているので、自習でも躓きにくくなっています。

小学校の算数における資料の調べ方から始めて、高等学校の数学１における「データの分析」までを扱った「統計分野」の参考書。中学校までの復習を扱った「ホームルーム」、数学１データの分析で学習する内容をていねいに説明した「授業」、あらゆる問題形式（センター形式や記述式）を演習する「講習」の３部構成。好評だった初版のよいところを活かしつつ、2015年から実施された現行課程下の入試でのセンター試験の問題を追加したほか、私大・国公立入試で出題された問題のうち、とくに重要かつ今後の出題が見込まれるものを収録。