07/17/2021 数学3
今回は定積分と不等式の証明について学習しましょう。定積分と不等式を扱った問題は入試でも頻出です。
以前の記事で扱った区分求積法の理解に多少は役立つので、しっかりマスターしておきたい単元です。
定積分と不等式の証明を扱った問題を解いてみよう さっそく問題を解いてみましょう。まずは自力で挑戦してみましょう。
問題
\begin{align*}
&\text{$2$ 以上の自然数 $n$ について、不等式} \\[ 5pt ]
&\quad \log {(n+1)} \lt 1 + \frac{1}{2} + \frac{1}{3} + \ \cdots \cdots \ + \frac{1}{n} \lt 1 + \log n \\[ 10pt ]
&\text{が成り立つことを示せ。}
\end{align*}
与えられた不等式をよく観察しよう 非常にシンプルな問題なので、情報が少ないと感じるかもしれません。それでもよく観察して解法のヒントを探さなければなりません。
本問では、不等式の中央、特に最後の項1/n に注目します。
中央の式において、分母は1,2,3,……,nと変化しています。このように変化する関数を考えると、反比例の式y=1/x を思いつきます。
この問題では、扱う関数の式を決定する のが最初のステップです。グラフと定積分を利用することによって、不等式を導出します。
不等式の中央の式、特に最後の項に注目して、関数の式を決めよう。
図形の面積の関係を考えよう 定積分は図形の面積を求めることができます。このことを利用して、大小関係のある図形を探します。
隣り合う区間で面積の大小関係を考える
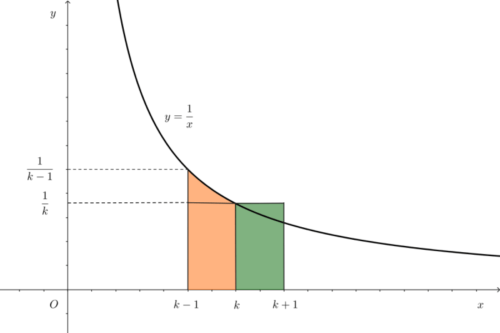
上図は反比例y=1/xのグラフにおける定積分と、長方形の面積との関係を考えています。もう少し分かるように描き分けてみましょう。
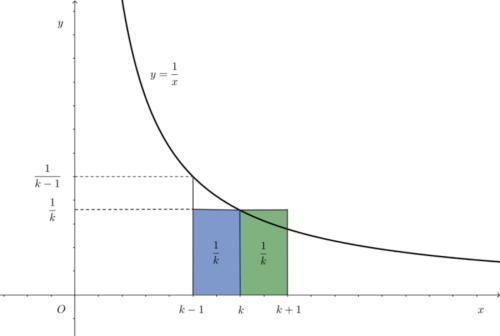
横1、縦1/kの長方形
上図は区間k-1≦x≦kと区間k≦x≦k+1でそれぞれ面積が1/kとなる長方形 を考えています。どちらの区間でも横1、縦1/kの長方形です。 縦はグラフ上の点のy座標を使うので注意しましょう。
また、両区間における定積分を図示すると以下のようになります。
両区間の定積分による面積
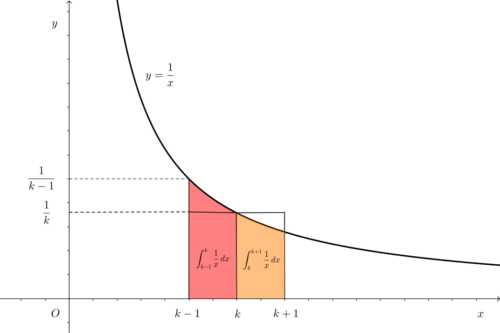
区間k-1≦x≦kと区間k≦x≦k+1でそれぞれ定積分 すると以下のように表せます。この定積分によって、グラフとx軸に挟まれた部分の面積 が得られます。
各区間における定積分
\begin{align*}
&\text{$k-1 \leqq x \leqq k$ における定積分} \\[ 5pt ]
&\quad \int_{k-1}^k \frac{1}{x} dx \\[ 10pt ]
&\text{$k \leqq x \leqq k+1$ における定積分} \\[ 5pt ]
&\quad \int_k^{k+1} \frac{1}{x} dx
\end{align*}
図を見ると分かるように、反比例のグラフy=1/xは、x>0では単調減少 します。ですから、長方形の面積と定積分で得られる面積の間には、必ず大小関係があります。
反比例のグラフはx>0で単調減少
図を確認しながら、2つの図形の面積の大小関係を不等式で表します。定積分による面積の方が長方形よりも大きくなります。
定積分と長方形の面積の関係
\begin{align*}
&\text{図より} \\[ 5pt ]
&\quad \frac{1}{k} \lt \int_{k-1}^k \frac{1}{x} dx \quad \text{$\cdots$ ①} \\[ 10pt ]
&\quad \int_k^{k+1} \frac{1}{x} dx \lt \frac{1}{k} \quad \text{$\cdots$ ②}
\end{align*}
このように定積分が図形の面積を表す ことを利用して、他の図形との面積の大小関係から不等式を導出することができます。
他の区間での面積の大小関係も考えよう 区間k-1≦x≦kと区間k≦x≦k+1で考えましたが、他の区間でも成り立つかを考えます。
①,②式は任意のkについて成り立つ式です。ですから、これらの不等式は、単調減少するグラフであればどの区間でも成り立つ ことが分かります。
①式において、k=2,3,……,nのときでも不等式は成り立ちます。ただし、k=2から始まるのは、定積分ができ、長方形が作れることが条件なので、x>0とk-1>0を考慮しています。
そして、これらの不等式の各辺を加えて整理し、少し手を加えると③式を得ることができます。
全区間での面積の関係
\begin{align*}
&\quad \frac{1}{k} \lt \int_{k-1}^k \frac{1}{x} dx \quad \cdots \text{①} \\[ 10pt ]
&\text{①より $k=2 \ , \ 3 \ , \cdots , \ n$ のとき} \\[ 5pt ]
&\quad \frac{1}{2} \lt \int_1^2 \frac{1}{x} dx \\[ 10pt ]
&\quad \frac{1}{3} \lt \int_2^3 \frac{1}{x} dx \\[ 10pt ]
&\qquad \vdots \\[ 10pt ]
&\quad \frac{1}{n} \lt \int_{n-1}^n \frac{1}{x} dx \\[ 10pt ]
&\text{が成り立つ。これらの各辺を加えると} \\[ 5pt ]
&\quad \frac{1}{2} + \frac{1}{3} + \ \cdots \cdots \ + \frac{1}{n} \lt \int_1^2 \frac{1}{x} dx + \int_2^3 \frac{1}{x} dx + \ \cdots \cdots \ + \int_{n-1}^n \frac{1}{x} dx \\[ 10pt ]
&\text{右辺を整理すると} \\[ 5pt ]
&\quad \frac{1}{2} + \frac{1}{3} + \ \cdots \cdots \ + \frac{1}{n} \lt \int_1^n \frac{1}{x} dx \\[ 10pt ]
&\text{また、両辺に $1$ を加えると} \\[ 5pt ]
&\quad 1 + \frac{1}{2} + \frac{1}{3} + \ \cdots \cdots \ + \frac{1}{n} \lt 1 + \int_1^n \frac{1}{x} dx \quad \cdots \text{③}
\end{align*}
両辺に1を加えて③式を導出したのは、与式の中央の式と同じにするためです。
また、いくつかの不等式の左辺どうし、右辺どうしを加える計算は不等式の性質 を利用したものです。数学1A,2Bでもよく利用するので、使いこなせるようにしておきましょう。
不等式の性質
\begin{align*}
&\text{$A \ , \ B \ , \ C \ , \ D$ について} \\[ 5pt ]
&\quad A \lt B \ , \ C \lt D \\[ 10pt ]
&\text{が成り立つとき、} \\[ 5pt ]
&\quad A + C \lt B + D \\[ 10pt ]
&\text{が成り立つ。}
\end{align*}
また、②式において、k=1,2,……,nのときの不等式の各辺を加えると、新たな不等式(④式)を得ることができます。
全区間での面積の関係
\begin{align*}
&\quad \int_k^{k+1} \frac{1}{x} dx \lt \frac{1}{k} \quad \cdots \text{②} \\[ 10pt ]
&\text{②より $k=1 \ , \ 2 \ , \cdots , \ n$ のとき} \\[ 5pt ]
&\quad \int_1^2 \frac{1}{x} dx \lt 1 \\[ 10pt ]
&\quad \int_2^3 \frac{1}{x} dx \lt \frac{1}{2} \\[ 10pt ]
&\qquad \vdots \\[ 10pt ]
&\quad \int_n^{n+1} \frac{1}{x} dx \lt \frac{1}{n} \\[ 10pt ]
&\text{が成り立つ。これらの各辺を加えると} \\[ 5pt ]
&\quad \int_1^2 \frac{1}{x} dx + \int_2^3 \frac{1}{x} dx + \ \cdots \cdots \ + \int_n^{n+1} \frac{1}{x} dx \lt 1 + \frac{1}{2} + \frac{1}{3} + \ \cdots \cdots \ + \frac{1}{n} \\[ 10pt ]
&\text{左辺を整理すると} \\[ 10pt ]
&\quad \int_1^{n+1} \frac{1}{x} dx \lt 1 + \frac{1}{2} + \frac{1}{3} + \ \cdots \cdots \ + \frac{1}{n} \quad \cdots \text{④}
\end{align*}
さいごに③,④式の定積分を計算します。
定積分の計算
\begin{align*}
&\quad 1 + \frac{1}{2} + \frac{1}{3} + \ \cdots \cdots \ + \frac{1}{n} \lt 1 + \int_1^n \frac{1}{x} dx \quad \cdots \text{③} \\[ 10pt ]
&\quad \int_1^{n+1} \frac{1}{x} dx \lt 1 + \frac{1}{2} + \frac{1}{3} + \ \cdots \cdots \ + \frac{1}{n} \quad \cdots \text{④} \\[ 10pt ]
&\text{③の定積分について} \\[ 5pt ]
&\quad \int_1^n \frac{1}{x} dx = \Bigl[ \log |x| \Bigr]_1^n = \log n \\[ 10pt ]
&\text{よって、③は} \\[ 5pt ]
&\quad 1 + \frac{1}{2} + \frac{1}{3} + \ \cdots \cdots \ + \frac{1}{n} \lt 1 + \log n \quad \cdots \text{⑤} \\[ 10pt ]
&\text{また、④の定積分について} \\[ 5pt ]
&\quad \int_1^{n+1} \frac{1}{x} dx = \Bigl[ \log |x| \Bigr]_1^{n+1} = \log {(n+1)} \\[ 10pt ]
&\text{よって、④は} \\[ 5pt ]
&\quad \log {(n+1)} \lt 1 + \frac{1}{2} + \frac{1}{3} + \ \cdots \cdots \ + \frac{1}{n} \quad \cdots \text{⑥}
\end{align*}
定積分を計算すると、与えられた不等式の左側や右側と同じものが出てきました。⑤,⑥式を1つの不等式にまとめると、与えられた不等式を導くことができます。
不等式の証明と言えば、左辺と右辺の差をとって正負を調べるのが基本的な解法です。しかし、積分が含まれる不等式の場合、面積の大小関係 を利用することが多いのが特徴です。自分で不等式を作りあげるイメージをもつと良いかもしれません。
上述した内容を記述すれば答案を作成できます。しかし、かなり長い答案になってしまいます。ですから、ある程度は省略する必要があります。次は答案を推敲してみましょう。