数学２
今回は、２点間の距離と三角形の形状について学習しましょう。平面上の２点間の距離は、図形の辺の長さに応用されます。
２点間の距離から、座標平面上にある図形の辺の長さを知り、その結果、図形の形状を調べることができます。
ここでは、三角形の形状について調べたり、特定の三角形になるための条件を考えたりします。
平面上の２点間の距離
平面上にある点があるとき、その位置は座標によって定められます。そして、位置情報である座標によって、２点間の距離を求めることができます。
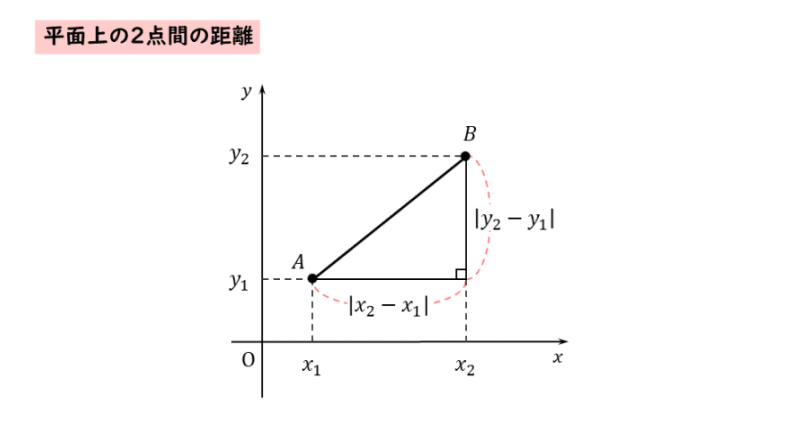平面上の２点間の距離
平面上にある２点間の距離を求めるには、数直線上の２点間の距離と三平方の定理とを組み合わせます。
平面上の２点間の距離 1⃣
\begin{align*}
&\text{座標平面上の $2$ 点 $A \ (x_{\scriptsize{1}} \ , y_{\scriptsize{1}}) \ , \ B \ (x_{\scriptsize{2}} \ , \ y_{\scriptsize{2}})$ 間の} \\[ 5pt ]
&\text{距離 $AB$ は} \\[ 7pt ]
&\quad AB=\sqrt{\left(x_{\scriptsize{2}}-x_{\scriptsize{1}} \right)^{\scriptsize{2}}+\left(y_{\scriptsize{2}}-y_{\scriptsize{1}} \right)^{\scriptsize{2}}}
\end{align*}
特に、原点との距離は以下の通りです。
平面上の２点間の距離 2⃣
\begin{align*}
&\text{座標平面上の $2$ 点 $O \ (0 \ , \ 0) \ , \ B \ (x_{\scriptsize{1}} \ , \ y_{\scriptsize{1}})$ 間の} \\[ 5pt ]
&\text{距離 $OA$ は} \\[ 7pt ]
&\quad OA=\sqrt{{x_{\scriptsize{1}}}^{\scriptsize{2}}+{y_{\scriptsize{1}}}^{\scriptsize{2}}}
\end{align*}
公式の導出手順などは、前回の記事ですでに学習しています。
図形の形状
図形の形状を知るために有効なことは、辺の長さや角の大きさを調べることです。ここでは、辺の長さを調べます。
出題される図形として考えられるのは、三角形や四角形です。三角形や四角形の定義については中学で学習します。それぞれの定義をしっかりと確認しておきたいところです。
たとえば、三角形であれば３辺の長さを調べます。３辺の長さの関係によっては、特別な三角形になっていることが分かります。
３辺の関係と三角形の形状
- ３辺が等しい ⇔ 正三角形
- ２辺が等しい ⇔ 二等辺三角形
- 三平方の定理が成り立つ ⇔ 直角三角形
なお、形状によっては但し書きが必要になります。たとえば、三角形の形状が二等辺三角形であるとき、長さの等しい２辺を、また、直角三角形であるとき、直角である内角を明記します。忘れないようにしましょう。
出題される問題では、三角形の形状は上述のいずれかになっていることがほとんどです。このような問題で３辺の長さを求めます。このとき、２点間の距離を利用して、線分、つまり辺の長さを求めます。
三角形の形状を調べてみよう
例題
\begin{align*}
&\text{次の問に答えよ。} \\[ 5pt ]
&(1) \quad \text{$3$ 点 $A(1 \ , \ -1) \ , \ B(4 \ , \ 1) \ , \ C(-1 \ , \ 2)$ を頂点とする} \\[ 5pt ]
&\qquad \text{$\triangle {ABC}$ はどのような三角形か。} \\[ 10pt ]
&(2) \quad \text{$A(1 \ , \ 0) \ , \ B(0 \ , \ 3) \ , \ C(a \ , \ b)$ を頂点とする $\triangle {ABC}$ が} \\[ 5pt ]
&\qquad \text{正三角形となるように、$a \ , \ b$ の値を定めよ。}
\end{align*}
例題(1)の解答・解説
例題(1)
\begin{align*}
&\text{次の問に答えよ。} \\[ 5pt ]
&\text{$3$ 点 $A(1 \ , \ -1) \ , \ B(4 \ , \ 1) \ , \ C(-1 \ , \ 2)$ を頂点とする} \\[ 5pt ]
&\text{$\triangle {ABC}$ はどのような三角形か。}
\end{align*}
△ＡＢＣにおいて、３つの頂点の座標がすべて与えられています。３辺の長さを求めることができます。
２点間の距離を利用して、３辺の長さを調べます。
例題(1)の解答例 1⃣
\begin{align*}
&\quad A(1 \ , \ -1) \ , \ B(4 \ , \ 1) \ , \ C(-1 \ , \ 2) \\[ 7pt ]
&\text{$3$ 辺の長さについて} \\[ 5pt ]
&\quad AB^{\scriptsize{2}} = \left(4-1 \right)^{\scriptsize{2}}+\left\{1-(-1) \right\}^{\scriptsize{2}} \\[ 7pt ]
&\quad BC^{\scriptsize{2}}=\left(-1-4 \right)^{\scriptsize{2}}+\left(2-1 \right)^{\scriptsize{2}} \\[ 7pt ]
&\quad CA^{\scriptsize{2}}=\left\{1-(-1) \right\}^{\scriptsize{2}}+\left(-1-2 \right)^{\scriptsize{2}} \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad AB^{\scriptsize{2}} = 13 \\[ 7pt ]
&\quad BC^{\scriptsize{2}} = 26 \\[ 7pt ]
&\quad CA^{\scriptsize{2}} = 13
\end{align*}
３辺の長さを求めるときは、２乗した値で構いません。２乗した値の場合、根号がないので計算しやすいのが利点です。それに、三平方の定理が成り立つかどうかの判断もしやすくなります。
３辺の長さを比べて、三角形の形状を特定します。
例題(1)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad AB^{\scriptsize{2}} = 13 \\[ 7pt ]
&\quad BC^{\scriptsize{2}} = 26 \\[ 7pt ]
&\quad CA^{\scriptsize{2}} = 13 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad AB=CA \ , \ BC^{\scriptsize{2}}=CA^{\scriptsize{2}}+AB^{\scriptsize{2}} \\[ 7pt ]
&\text{したがって、$\triangle {ABC}$ は $\angle A=90^{\circ}$ の} \\[ 5pt ]
&\text{直角二等辺三角形である。}
\end{align*}
３辺の長さの関係を調べるとき、三平方の定理が成り立つことの確認をよく忘れます。それを防ぐには、辺の長さを２乗した形で計算した方が無難です。
例題(2)の解答・解説
例題(2)
\begin{align*}
&\text{次の問に答えよ。} \\[ 5pt ]
&\text{$A(1 \ , \ 0) \ , \ B(0 \ , \ 3) \ , \ C(a \ , \ b)$ を頂点とする $\triangle {ABC}$ が} \\[ 5pt ]
&\text{正三角形となるように、$a \ , \ b$ の値を定めよ。}
\end{align*}
例題(2)では条件があります。この条件を考慮すると、３辺の関係について等式を導くことができるはずです。
例題(2)の解答例 1⃣
\begin{align*}
&\quad A(1 \ , \ 0) \ , \ B(0 \ , \ 3) \ , \ C(a \ , \ b) \\[ 7pt ]
&\text{$\triangle {ABC}$ が正三角形であるための条件は} \\[ 5pt ]
&\quad AB=BC=CA \\[ 7pt ]
&\text{すなわち} \\[ 5pt ]
&\quad AB^{\scriptsize{2}}=BC^{\scriptsize{2}}=CA^{\scriptsize{2}}
\end{align*}
得られた等式から新たに方程式を導きます。未知の文字は２つあるので、方程式が２つ必要です。
例題(2)の解答例 2⃣
\begin{align*}
&\quad A(1 \ , \ 0) \ , \ B(0 \ , \ 3) \ , \ C(a \ , \ b) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad AB^{\scriptsize{2}}=BC^{\scriptsize{2}}=CA^{\scriptsize{2}} \\[ 7pt ]
&\text{$AB^{\scriptsize{2}}=BC^{\scriptsize{2}}$ より} \\[ 5pt ]
&\quad \left(0-1 \right)^{\scriptsize{2}}+\left(3-0 \right)^{\scriptsize{2}}=\left(a-0 \right)^{\scriptsize{2}}+\left(b-3 \right)^{\scriptsize{2}} \\[ 7pt ]
&\quad 1+9 = a^{\scriptsize{2}}+\left(b-3 \right)^{\scriptsize{2}} \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad a^{\scriptsize{2}}+\left(b-3 \right)^{\scriptsize{2}}=10 \quad \cdots \text{①} \\[ 7pt ]
&\text{また、$BC^{\scriptsize{2}}=CA^{\scriptsize{2}}$ より} \\[ 5pt ]
&\quad a^{\scriptsize{2}}+\left(b-3 \right)^{\scriptsize{2}}=\left(a-1 \right)^{\scriptsize{2}}+\left(b-0 \right)^{\scriptsize{2}} \\[ 7pt ]
&\quad a^{\scriptsize{2}}+b^{\scriptsize{2}}-6b+9 =a^{\scriptsize{2}}-2a+1+b^{\scriptsize{2}} \\[ 7pt ]
&\quad 2a=6b-8 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad a=3b-4 \quad \cdots \text{②}
\end{align*}
①，②式から連立方程式を解きます。加減法は無理なので、代入法で解きます。
例題(2)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad a^{\scriptsize{2}}+\left(b-3 \right)^{\scriptsize{2}}=10 \quad \cdots \text{①} \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad a=3b-4 \quad \cdots \text{②} \\[ 7pt ]
&\text{②を①に代入すると} \\[ 5pt ]
&\quad \left(3b-4 \right)^{\scriptsize{2}}+\left(b-3 \right)^{\scriptsize{2}}=10 \\[ 7pt ]
&\text{これを整理すると} \\[ 5pt ]
&\quad 2b^{\scriptsize{2}}-6b+3=0 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad b=\frac{3 \pm \sqrt{3}}{2} \\[ 7pt ]
&\text{これと②より} \\[ 5pt ]
&\quad a = 3 \cdot \frac{3 \pm \sqrt{3}}{2}-4 \\[ 7pt ]
&\text{これを整理すると} \\[ 5pt ]
&\quad a = \frac{1 \pm 3 \sqrt{3}}{2} \\[ 7pt ]
&\text{したがって} \\[ 5pt ]
&\quad (a \ , \ b)=\left(\frac{1 \pm 3 \sqrt{3}}{2} \ , \ \frac{3 \pm \sqrt{3}}{2} \right) \quad \text{（複合同順）}
\end{align*}
作図すると分かりますが、頂点の位置がすべて決まっていない場合、複数の三角形ができることがあります。
例題(2)では、頂点Ａ，Ｂの位置が決まっているので、辺ＡＢは固定されます。しかし、頂点Ｃの位置は決まっていません。ですから、辺ＡＢに関して対称な正三角形を作ることができます。
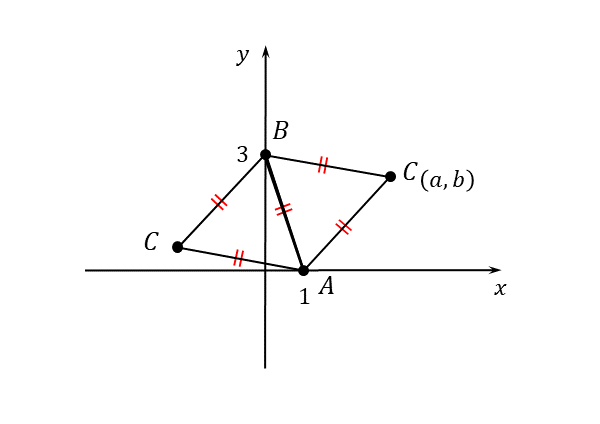点Ｃの位置は２通りある
作図の利点は、答えを予想できたり、問題の意図をより深く読み取れたりすることです。点Cの位置が複数あることを予想できていれば、方程式の解が複数あっても慌てずに済みます。
作図することで情報を増やして、少しでも解答への道筋を立てておこう。
次は、２点間の距離と三角形の形状を扱った問題を実際に解いてみましょう。
