式と証明｜割り算と整式の決定について

06/07/2021数学２

今回は、割り算と整式の決定について学習しましょう。割り算の結果から、割られる整式や割る整式を求めます。

ここでも整式の割り算をしなければならないので、ミスなく筆算しなければなりません。

1. 割り算と整式の決定
2. 例題を解いてみよう
3. 整式の割り算を扱った問題を解いてみよう
- 3.1. 問(1)の解答・解説
- 3.2. 問(2)の解答・解説
4. Recommended books
- 4.1. オススメその１『合格る計算数学１・A・２・Ｂ』
- 4.2. オススメその２『鉄緑会基礎力完成数学Ⅰ・Ａ＋Ⅱ・Ｂ』
5. さいごにもう一度まとめ

割り算と整式の決定

たとえば、以下のような割り算が行われたとします。

例題

$(1)$ 整式 $A$ を整式 $2x^{\scriptsize{2}}-1$ で割ると、商が $2x-1$で、余りが $x-2$ であるとき、整式 $A$ を求めよ。

$(2)$ 整式 $8x^{\scriptsize{3}}-18x^{\scriptsize{2}}+19x+1$ を整式 $B$ で割ると、商が $4x-3$で、余りが $2x+7$ であるとき、整式 $B$ を求めよ。

例題は、割り算の結果を利用して、割られる式や割る式を求める問題です。このような問題では、割り算の基本公式を利用して求めます。

割り算の基本公式

同じ $1$ つの文字についての $2$ つの整式 $A \ , \ B \ (B \neq 0)$ において、$A$ を $B$ で割ったときの商を $Q$、余りを $R$ とすると

\begin{equation*} \quad A = BQ + R \end{equation*}

ただし、$R$ は $0$ か、$B$ より次数の低い整式

ことばで表せば、以下のようになります。

割り算の基本公式

(割られる式) ＝ (割る式) × (商) + (余り)

問題によっては、求めるものが商になるかもしれませんが、商や余りなどの情報が与えられていれば、基本公式を利用できないか考えましょう。

例題を解いてみよう

例題を使って、解く過程を確認してみましょう。

例題(1)

整式 $A$ を整式 $2x^{\scriptsize{2}}-1$ で割ると、商が $2x-1$で、余りが $x-2$ であるとき、整式 $A$ を求めよ。

与えられた式のそれぞれを、割り算の基本公式に代入します。

例題(1)の解答例

\begin{align*} &\text{この割り算について、次の等式が成り立つ。} \\[ 5pt ] &\quad A = (2x^{\scriptsize{2}}-1)(2x-1) + (x-2) \\[ 7pt ] &\text{この等式の右辺を整理すると} \\[ 5pt ] &\quad A = (4x^{\scriptsize{3}}-2x^{\scriptsize{2}}-2x+1) + (x-2) \\[ 7pt ] &\text{よって} \\[ 5pt ] &\quad A = 4x^{\scriptsize{3}}-2x^{\scriptsize{2}}-x-1 \end{align*}

多項式を代入するとき、式をかっこでくくっておくと代入ミスを減らせます。また、掛け算の記号なども追記しておくと良いでしょう。

例題(2)

整式 $8x^{\scriptsize{3}}-18x^{\scriptsize{2}}+19x+1$ を整式 $B$ で割ると、商が $4x-3$で、余りが $2x+7$ であるとき、整式 $B$ を求めよ。

例題(2)も同じ要領で解きます。与えられた式のそれぞれを、割り算の基本公式に代入します。

例題(2)の解答例 1⃣

\begin{align*} &\text{この割り算について、次の等式が成り立つ。} \\[ 5pt ] &\quad 8x^{\scriptsize{3}}-18x^{\scriptsize{2}}+19x+1 = B \times (4x-3) + (2x+7) \\[ 7pt ] &\text{この等式を変形すると} \\[ 5pt ] &\quad 8x^{\scriptsize{3}}-18x^{\scriptsize{2}}+17x-6 = B \times (4x-3) \end{align*}

例題(2)で気をつけたいのは、整式Ｂを求める割り算をする前に、余りを処理することです。割られる式から余りを引いたので、整式Ｂを求める割り算は割り切れることに注意しましょう。

例題(2)の解答例 2⃣

\begin{align*} &\quad \vdots \\[ 7pt ] &\quad 8x^{\scriptsize{3}}-18x^{\scriptsize{2}}+17x-6 = B \times (4x-3) \end{align*}

左辺を $4x-3$ で割ると、割り切れ、その商が $B$ となる。

\begin{align*} &\text{筆算すると} \\[ 5pt ] &\quad B = 4x^{\scriptsize{2}}-3x+2 \end{align*}

次は、整式の割り算を実際に解いてみましょう。

整式の割り算を扱った問題を解いてみよう

次の問題を解いてみましょう。

問

$(1) \quad A$ を $2x^{\scriptsize{2}}-x+4$ で割ると、商が $2x-1$、余りが $x-1$

$(2) \quad x^{\scriptsize{3}}+x+10$ を $B$ で割ると、商が $x/2+1$、余りが $x+2$

整式によっては、筆算しても計算ミスをしやすい割り算があります。自分なりに工夫しながら、丁寧に計算しましょう。

問(1)の解答・解説

問(1)

$A$ を $2x^{\scriptsize{2}}-x+4$ で割ると、商が $2x-1$、余りが $x-1$

割り算の基本公式に代入します。代入できたら整理します。

問(1)の解答例

\begin{align*} &\text{この割り算について、次の等式が成り立つ。} \\[ 5pt ] &\quad A = (2x^{\scriptsize{2}}-x+4)(2x-1) + (x-1) \\[ 7pt ] &\text{この等式の右辺を整理すると} \\[ 5pt ] &\quad A = (4x^{\scriptsize{3}}-4x^{\scriptsize{2}}+9x-4) + (x-1) \\[ 7pt ] &\text{よって} \\[ 5pt ] &\quad A = 4x^{\scriptsize{3}}-4x^{\scriptsize{2}}+10x-5 \end{align*}

どの式も欠けた次数がなく、降べきの順に整理されていたので、展開と同類項の整理を丁寧に行えば間違えることはないでしょう。

割り算の基本公式を用いた問題の中でも基本レベルなので、確実にマスターしておきましょう。

問(2)の解答・解説

問(2)

$x^{\scriptsize{3}}+x+10$ を $B$ で割ると、商が $x/2+1$、余りが $x+2$

２次の項や１次の項が欠けた式が与えられているので注意しましょう。問(1)と同じ要領で解きます。

問(2)の解答例 1⃣

\begin{align*} &\text{この割り算について、次の等式が成り立つ。} \\[ 5pt ] &\quad x^{\scriptsize{3}}+x+10 = B \times \left(\frac{x}{2}+1 \right) + (x+2) \\[ 7pt ] &\text{この等式を変形すると} \\[ 5pt ] &\quad x^{\scriptsize{3}}+8 = B \times \left(\frac{x}{2}+1 \right) \end{align*}

例題(2)と同じように、このまま商で割り算しても良いのですが、係数が分数であることに注目します。

係数が分数だと、少々面倒な割り算になります。そこで等式であることを利用して、係数を整数にしておきます。

問(2)の解答例 2⃣

\begin{align*} &\quad \vdots \\[ 7pt ] &\quad x^{\scriptsize{3}}+8 = B \times \left(\frac{x}{2}+1 \right) \\[ 7pt ] &\text{さらに両辺に $2$ を掛けて} \\[ 5pt ] &\quad 2x^{\scriptsize{3}}+16 = B \times (x+2) \end{align*}

この変形は等式だからできる変形です。いつでもできるわけではないので気をつけましょう。

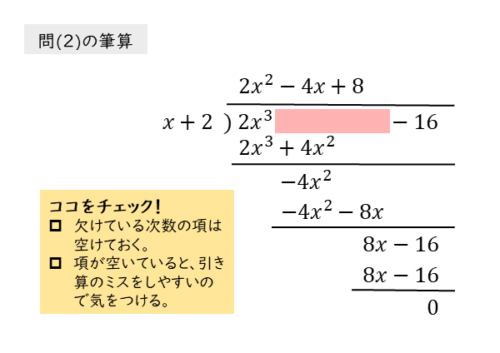
筆算して整式Ｂを求めます。

問(2)の解答例 3⃣

\begin{align*} &\quad \vdots \\[ 7pt ] &\quad 2x^{\scriptsize{3}}+16 = B \times (x+2) \\[ 7pt ] &\text{筆算すると} \\[ 5pt ] &\quad B = 2x^{\scriptsize{2}}-4x+8 \end{align*}