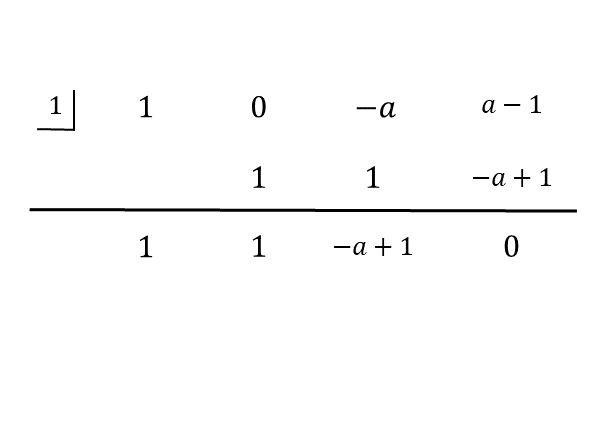数学２
今回は、割られる式や余りの決定について学習しましょう。ここでは、整式を割り算したときの、割られる式や余りについて考えます。割り算に関する情報をもとに、割られる式や余りを決定します。
割られる式と余りの決定
割り算の基本公式
整式の割り算に関する問題では、割り算の基本公式をよく利用します。これまで何度も見聞きしていますが、割り算の基本公式を確認しておきましょう。
割り算の基本公式
\begin{align*}
&\text{同じ $1$ つの文字についての $2$ つの整式} \\[ 5pt ]
&\quad A \ , \ B \quad (B \neq 0) \\[ 7pt ]
&\text{において、$A$ を $B$ で割ったときの商を $Q$} \\[ 5pt ]
&\text{余りを $R$ とすると} \\[ 5pt ]
&\quad A = BQ + R \\[ 7pt ]
&\text{ただし、$R$ は $0$ か、$B$ より次数の低い整式}
\end{align*}
割られる整式Ａは、割る整式Ｂ、商Ｑ、余りＲの３つを用いて表されます。以下、整式のことを単に式と言うことがあります。
割り算の基本公式
割り算の基本公式を利用するとき、特に余りの次数のことを忘れないようにしましょう。
余りと割る式の次数の関係
\begin{align*}
&\text{余り $R$ と割る式 $B$ の次数の関係は} \\[ 5pt ]
&\quad ( \ \text{余り $R$ の次数} \ ) \ \lt \ ( \ \text{割る式 $B$ の次数} \ ) \\[ 7pt ]
&\text{となる。}
\end{align*}
余りの次数に慣れてきたら、商の次数にも目を向けましょう。たとえば、３次式を１次式で割る場合、商は２次式となります。ちなみに、余りは定数となります。
整式の割り算では、割る式や余りなどの次数に注目することが大切です。
剰余の定理
余りの情報が与えられていれば、剰余の定理のことを意識しましょう。
剰余の定理
\begin{align*}
&\text{1⃣ 整式 $P(x)$ を $1$ 次式 $x-k$ で割ったときの余りは} \\[ 5pt ]
&\quad P(k) \quad \text{（剰余の定理）} \\[ 10pt ]
&\text{2⃣ 整式 $P(x)$ を $1$ 次式 $ax+b$ で割ったときの余りは} \\[ 5pt ]
&\quad P \left(-\frac{b}{a} \right)
\end{align*}
剰余の定理を利用できるのは、割る式が１次式のときだけです。しかし、筆算をせずに余りを調べることができるので、非常に便利な定理です。
整式の割り算を扱った問題では、以上の３つの事柄を上手に組み合わせて解いていきます。使い方をそれぞれマスターしておきましょう。
整式の割り算を扱った問題に出会ったら
- 整式を割り算の基本公式で表す。
- 割られる式、割る式、商、余りの次数を確認する。(特に、余りの次数)
- 余りの情報には剰余の定理を利用する。
割られる式や余りを決定してみよう
次の例題を考えてみましょう。
例題
\begin{align*}
(1) &\quad \text{$f(x)=x^{\scriptsize{3}}-ax+b$ が $(x-1)^{\scriptsize{2}}$ で割り切れる} \\[ 5pt ]
&\quad \text{とき、定数 $a \ , \ b$ の値を求めよ。} \\[ 10pt ]
(2) &\quad \text{$n$ を $2$ 以上の整数とするとき、$x^{\scriptsize{n}}-1$ を} \\[ 5pt ]
&\quad \text{$(x-1)^{\scriptsize{2}}$ で割ったときの余りを求めよ。}
\end{align*}
例題(1)の解答・解説
例題(1)
\begin{align*}
&\text{$f(x)=x^{\scriptsize{3}}-ax+b$ が $(x-1)^{\scriptsize{2}}$ で割り切れる} \\[ 5pt ]
&\text{とき、定数 $a \ , \ b$ の値を求めよ。}
\end{align*}
例題(1)は、割られる式（の係数や定数項）を決定する問題です。与えられた情報を整理してみましょう。
例題(1)で与えられた情報
- 割られる式：３次式ｆ(ｘ)
- 割る式：２次式(ｘ－１)2
- 商：不明
- ３次式を２次式で割ると割り切れる＝余りは０
- 割られる３次式の係数や定数項を決定する
３次式を２次式(ｘ－１)2で割ると割り切れるので、３次式は２次式(ｘ－１)2を因数にもつことが分かります。２次式(ｘ－１)2は、２つの１次式ｘ－１を因数にもちます。このことから、３次式は２個のｘ－１を因数にもつと言えます。
３次式が１次式ｘ－１を因数にもつので、３次式を１次式ｘ－１で割ると割り切れます。つまり、３次式を１次式ｘ－１で割った余りは０です。
３次式を１次式で割った余りが分かったので、剰余の定理を利用します。
例題(1)の解答例 1⃣
\begin{align*}
&\quad f(x)=x^{\scriptsize{3}}-ax+b \\[ 7pt ]
&\text{$f(x)$ は $x-1$ で割り切れるので} \\[ 5pt ]
&\quad f(1)=0 \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad 1-a+b=0 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad b=a-1 \quad \cdots \text{①}
\end{align*}
定数ｂを定数ａを用いて表すことができました（①式）。これを３次式に代入して、文字の種類を減らします。文字の種類を減らすと、３次式の因数が分かりやすくなります。
例題(1)の解答例 2⃣
\begin{align*}
&\quad f(x)=x^{\scriptsize{3}}-ax+b \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad b=a-1 \quad \cdots \text{①} \\[ 7pt ]
&\text{①を $f(x)$ に代入すると} \\[ 5pt ]
&\quad f(x)=x^{\scriptsize{3}}-ax+a-1
\end{align*}
与えられた３次式は、１次式ｘ－１で割ると割り切れます。このとき、因数定理が成り立つので、因数分解できるはずです。組立除法で割り算して、商を調べます。
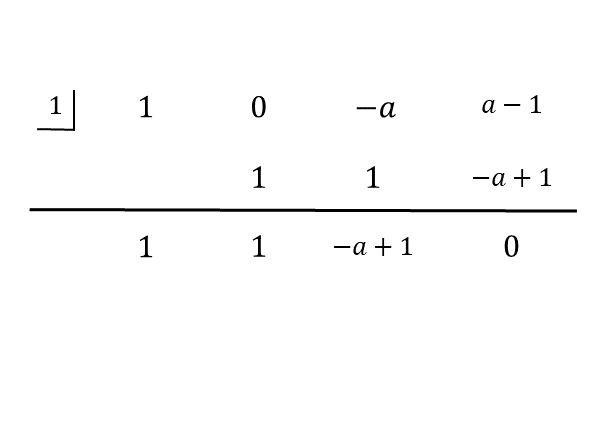例題(1)の組立除法 ２次の項がないことに注意しましょう。組立除法の結果を用いて、与えられた３次式を因数分解します。
例題(1)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad f(x)=x^{\scriptsize{3}}-ax+a-1 \\[ 7pt ]
&\text{これを因数分解すると} \\[ 5pt ]
&\quad f(x)=\left(x-1 \right) \left(x^{\scriptsize{2}}+x+1-a \right) \\[ 7pt ]
&\text{ここで} \\[ 5pt ]
&\quad g(x)=x^{\scriptsize{2}}+x+1-a
\end{align*}
最後の行では、商の２次式だけを取り出しています。２次式の因数を考えるためです。
与えられた３次式は、２つの１次式ｘ－１を因数にもつことが分かっています。すでに１つは割る式として出てきました。
１次式ｘ－１はまだ１つ残っていますが、残った１つは商の中にあります。商の２次式は、１次式ｘ－１を因数にもつので、１次式ｘ－１で割ると割り切れるはずです。
商の２次式において剰余の定理を利用します。
例題(1)の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad g(x)=x^{\scriptsize{2}}+x+1-a \\[ 7pt ]
&\text{$g(x)$ は $x-1$ で割り切れるので} \\[ 5pt ]
&\quad g(1)=0 \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad 1+1+1-a=0 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad a=3
\end{align*}
定数ａの値が分かりました。この値を①式に代入して、定数ｂの値を求めます。
例題(1)の解答例 5⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad b=a-1 \quad \cdots \text{①} \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad a=3 \\[ 7pt ]
&\text{これと①より} \\[ 5pt ]
&\quad b=2 \\[ 7pt ]
&\text{したがって} \\[ 5pt ]
&\quad a=3 \ , \ b=2
\end{align*}
割る式が２次式であれば、剰余の定理を利用できません。しかし、因数に着目すると、剰余の定理、または因数定理を利用できる余地が出てきます。
割る式が２次式であっても、１次式に分けて考えれば、剰余の定理や因数定理を利用できる。
例題(2)の解答・解説
例題(2)
\begin{align*}
&\text{$n$ を $2$ 以上の整数とするとき、$x^{\scriptsize{n}}-1$ を} \\[ 5pt ]
&\text{$(x-1)^{\scriptsize{2}}$ で割ったときの余りを求めよ。}
\end{align*}
例題(2)は、余りを決定する問題です。与えられた情報を整理してみましょう。
例題(2)で与えられた情報
- 割られる式：ｎ次式ｘn－１（ただし、ｎ≧２）
- 割る式：２次式(ｘ－１)2
- 商：不明
- ｎ次式を２次式で割ったときの余りを求める
２次式で割るので、余りは１次式または定数であることが分かります。
また、与えられたｎ次式にｘ＝１を代入すると、式の値が０となります。剰余の定理から、ｎ次式を１次式ｘ－１で割ったときの余りが０であることが分かります。さらに、因数定理が成り立つので、ｎ次式は１次式ｘ－１を因数にもつことが分かります。
商や余りを定義して、割り算の基本公式を利用します。
例題(2)の解答例 1⃣
\begin{align*}
&\quad x^{\scriptsize{n}}-1 \quad (n \geqq 2) \\[ 7pt ]
&\text{$x^{\scriptsize{n}}-1$ を $(x-1)^{\scriptsize{2}}$ で割ったときの商を $Q(x)$} \\[ 5pt ]
&\text{余りを $ax+b$ とする。} \\[ 5pt ]
&\text{このとき、次の等式} \\[ 5pt ]
&\quad x^{\scriptsize{n}}-1=\left(x-1 \right)^{\scriptsize{2}} \ Q(x)+ax+b \\[ 7pt ]
&\text{が成り立つ。} \\[ 5pt ]
\end{align*}
例題(1)と同じように、文字の種類を減らすことを考えましょう。
例題(2)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad x^{\scriptsize{n}}-1=\left(x-1 \right)^{\scriptsize{2}} \ Q(x)+ax+b \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\text{両辺に $x=1$ を代入すると} \\[ 5pt ]
&\quad 0=a+b \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad b=-a \quad \cdots \text{①}
\end{align*}
定数ｂを定数ａを用いて表すことができました（①式）。文字の種類が減ると、式を扱いやすくなります。
これを等式に代入します。左辺のｎ次式が１次式ｘ－１を因数にもつので、右辺も１次式ｘ－１を因数にもちます。因数定理が成り立つことを利用して、等式の右辺を変形します。
例題(2)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad x^{\scriptsize{n}}-1=\left(x-1 \right)^{\scriptsize{2}} \ Q(x)+ax+b \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad b=-a \quad \cdots \text{①} \\[ 7pt ]
&\text{これを等式に代入すると} \\[ 5pt ]
&\quad x^{\scriptsize{n}}-1=\left(x-1 \right)^{\scriptsize{2}} \ Q(x)+ax-a \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad x^{\scriptsize{n}}-1=\left(x-1 \right)^{\scriptsize{2}} \ Q(x)+a\left(x-1 \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad x^{\scriptsize{n}}-1=\left(x-1 \right) \left\{ \left(x-1 \right) \ Q(x)+a \right\}
\end{align*}
等式の右辺を変形できたのは、文字の種類を減らせたからです。文字の種類を減らすのは、できるだけ早く済ませましょう。
等式の右辺を見ると、１次式ｘ－１と、１次式ｘ－１で割ったときの商との積でｎ次式が表されていることが分かります。右辺の波カッコの中の多項式が、１次式ｘ－１で割ったときの商です。
例題(1)と同じように、商だけを取り出します。ｎ次式の因数分解についての知識を利用します（後述します）。
例題(2)の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad x^{\scriptsize{n}}-1=\left(x-1 \right) \left\{ \left(x-1 \right) \ Q(x)+a \right\} \\[ 7pt ]
&\text{ここで} \\[ 5pt ]
&\quad x^{\scriptsize{n}}-1=\left(x-1 \right)\left(x^{\scriptsize{n-1}}+x^{\scriptsize{n-2}}+x^{\scriptsize{n-3}}+ \cdots \cdots +x+1 \right) \\[ 7pt ]
&\text{であるので} \\[ 5pt ]
&\quad x^{\scriptsize{n-1}}+x^{\scriptsize{n-2}}+x^{\scriptsize{n-3}}+ \cdots \cdots +x+1=\left(x-1 \right)Q(x)+a
\end{align*}
等式なので左辺のｎ次式も変形しておかないと、商を抜き出すことができないことに注意しましょう。
ｎ次式を変形した後に、商（波カッコの中の多項式）についての等式が得られます。この等式の両辺にｘ＝１を代入します。
例題(2)の解答例 5⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad x^{\scriptsize{n-1}}+x^{\scriptsize{n-2}}+x^{\scriptsize{n-3}}+ \cdots \cdots +x+1=\left(x-1 \right)Q(x)+a \\[ 7pt ]
&\text{両辺に $x=1$ を代入すると} \\[ 5pt ]
&\quad 1+1+1+ \cdots \cdots +1+1=a \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad 1 \times n =a \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad a=n
\end{align*}
等式にｘ＝１を代入すると、左辺には１がｎ個並びます。両辺を整理すると、定数ａの値が分かります。
定数ａの値を①式に代入して定数ｂの値を求めると、ｎ次式を２次式で割ったときの余りが分かります。
例題(2)の解答例 6⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad b=-a \quad \cdots \text{①} \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad a=n \\[ 7pt ]
&\text{これと①より} \\[ 5pt ]
&\quad b=-n \\[ 7pt ]
&\text{したがって、求める余りは} \\[ 5pt ]
&\quad nx-n
\end{align*}
例題(1)，(2)に共通するのは、文字の種類を減らすことです。文字の種類を減らした後、割られる式を変形し、商だけに注目しています。大筋では違いはありません。
解答例4⃣でｎ次式の因数分解（等式の左辺）が出てきました。これは、３次式の因数分解で学習した公式を一般化したものです。
ｎ次式の因数分解
\begin{align*}
&\text{$a^{\scriptsize{n}}-b^{\scriptsize{n}}$ を因数分解すると} \\[ 5pt ]
&\quad a^{\scriptsize{n}}-b^{\scriptsize{n}}=\left(a-b \right)\left(a^{\scriptsize{n-1}}+a^{\scriptsize{n-2}}b+a^{\scriptsize{n-3}}b^{\scriptsize{2}}+ \cdots \cdots +ab^{\scriptsize{n-2}}+b^{\scriptsize{n-1}} \right) \\[ 7pt ]
&\text{ただし、$n$ は自然数。また、$a^{0}=1 \ , \ b^{0}=1$ である。} \\[ 7pt ]
&\text{$a=x \ , \ b=1$ のとき} \\[ 5pt ]
&\quad x^{\scriptsize{n}}-1=\left(x-1 \right)\left(x^{\scriptsize{n-1}}+x^{\scriptsize{n-2}}+x^{\scriptsize{n-3}}+ \cdots \cdots +x+1 \right) \\[ 7pt ]
&\text{特に $n=3$ のとき} \\[ 5pt ]
&\quad x^{\scriptsize{3}}-1=\left(x-1 \right)\left(x^{\scriptsize{2}}+x+1 \right)
\end{align*}
次は、割られる式や余りの決定を扱った問題を実際に解いてみましょう。
