場合の数|集合の要素の個数について

今回から数学Aになります。数学Aは、数学1に比べて計算力よりも思考力の方に力点を置いた分野ではないかと思われます。数学1のときよりも、考え方や発想の方を意識すると良いでしょう。
記事の画像が見辛いときはクリックすると拡大できます。
要素の個数を漏れなく数え上げよう
集合と要素
集合と要素については、数学1の「集合と論理」という単元ですでに学習しています。用語の定義や表し方などをきちんと覚えているでしょうか?
既習内容が前提となっているので、不安があれば確認しつつ予習・復習をしましょう。
集合の要素の書き表し方
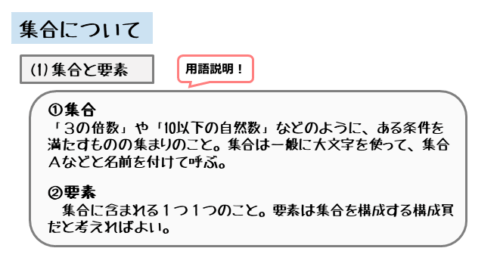
「集合と論理」という単元では、集合とそれに属する要素について学習しました。
集合とは、ある条件を満たすものの集まりです。また、要素とは、その集合に属するものです。
この単元では要素の個数に注目するので、集合の書き表し方がポイントになります。集合の書き表し方は2通りあります。
集合の書き表し方
- 条件で書き表す方法
- 要素を書き並べる方法
要素の個数を数え上げたいので、「要素を書き並べる方法」で集合を書き表しましょう。
要素の個数の表し方
集合が属する要素の個数は「n(集合の名称)」の形で表されます。
要素の個数の表し方
集合 $A$ の要素の個数が $k$ 個のとき
\begin{align*} \quad n(A)=k \end{align*}これまでは要素を書き並べるだけで済みましたが、これからは要素の個数にも注意する必要があります。
和集合や共通部分の要素の個数
集合ごとの要素の個数だけでなく、複数の集合の和集合や共通部分の要素の個数を求めることもあります。
和集合は、いくつかの集合において少なくとも一方に属する要素の集まりでした。集合A,Bの和集合をA⋃Bと表します。
また、共通部分は、いくつかの集合において共通な要素の集まりでした。集合A,Bの共通部分をA⋂Bと表します。
和集合の要素の個数は重なりに注意
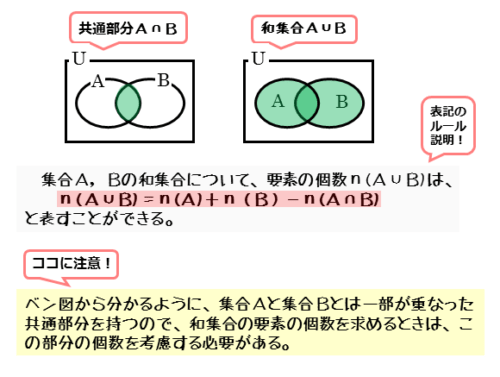
集合A,Bの和集合A⋃Bについて、その要素の個数n(A⋃B)は以下のように表されます。
和集合の要素の個数
$n(A \cup B)$ … 和集合 $A \cup B$ の要素の個数
$n(A)$ … 集合 $A$ の要素の個数
$n(B)$ … 集合 $B$ の要素の個数
$n(A \cap B)$ … 共通部分 $A \cap B$ の要素の個数
式を見ると、2つの集合A,Bの要素の個数の和から、共通部分の要素の個数を引いています。このことはベン図を描けばよく分かります。
要素が2つの集合A,Bに共通に属している場合、ベン図では2つの集合A,Bが重なります。この重なりが共通部分です。
共通部分の要素はどちらの集合にも属しているので、単に2つの集合A,Bの要素を合わせてしまうと、要素が重複します。
2つの集合A,Bの和集合の要素の個数を求めるには、共通部分のぶんだけ重複した要素の個数を除かなければなりません。
和集合の要素の個数を求めるとき、重なり(共通部分)に注意しよう。2つが重なると1つは余計。
補集合の要素の個数
補集合とは、集合に属さない要素の集まりのことです。たとえば、集合Aの補集合は、集合Aに属さない要素の集まりです。
集合Aの補集合について、その要素の個数は以下のように表されます。
補集合の要素の個数
\begin{align*} \quad n(\overline{A}) = n(U)-n(A) \end{align*}$n(\overline{A})$ … 補集合 $\overline{A}$ の要素の個数
$n(U)$ … 全体集合 $U$ の要素の個数
$n(A)$ … 集合 $A$ の要素の個数
補集合の要素の個数は、全体集合Uと集合Aを用いて間接的に求めます。
自分で集合を定義できるようになろう
要素の個数を求めることは決して難しいものではありません。ただ、問題では「~を集合Aとしなさい」などと指示されないことがよくあります。
そのような場合、必要に応じて「この条件に対応する集合をAとしよう」などと自分で定義する必要があります。複数の集合を扱う場合、定義せずに進めていくと混乱のもとになるので、集合に名前を付けた方が格段にミスが減ります。
次は要素の個数を扱った問題を実際に解いてみましょう。