図形と方程式|平行または垂直な直線の方程式について

今回は、平行な直線や垂直な直線の方程式について学習しましょう。2直線のうち、一方の直線の方程式から他方の直線の方程式を考えます。求めたい直線が通る点の座標なども与えられるので、それも加味します。
2直線の平行条件や垂直条件を利用するので、前回の内容を確認しながら進めていくと良いでしょう。
2直線の平行条件や垂直条件
2直線の平行条件は以下の通りでした。傾きを用いた式と、方程式の係数を用いた式の2種類があります。
2直線の平行条件
$2$ 直線
\begin{align*} &\quad y=m_{1}x+n_{1} \\[ 7pt ] &\quad y=m_{2}x+n_{2} \end{align*}が平行であるとき、平行条件は
\begin{align*} \quad m_{1}=m_{2} \end{align*}また、$2$ 直線
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}が平行であるとき、平行条件は
\begin{align*} \quad a_{1} b_{2}-a_{2} b_{1}=0 \end{align*}2直線の垂直条件は以下の通りでした。平行条件と同じように、傾きを用いた式と、方程式の係数を用いた式の2種類があります。
2直線の垂直条件
$2$ 直線
\begin{align*} &\quad y=m_{1}x+n_{1} \\[ 7pt ] &\quad y=m_{2}x+n_{2} \end{align*}が垂直であるとき、垂直条件は
\begin{align*} \quad m_{1} m_{2}=-1 \end{align*}また、$2$ 直線
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}が垂直であるとき、垂直条件は
\begin{align*} \quad a_{1} a_{2}+b_{1} b_{2}=0 \end{align*}これらの式は、与えられた直線の方程式が一般形かどうかで使い分けるのが一般的です。
平行または垂直な直線の方程式を求めてみよう
さっそく直線の方程式を求めてみましょう。
例題
次の直線の方程式を求めよ。
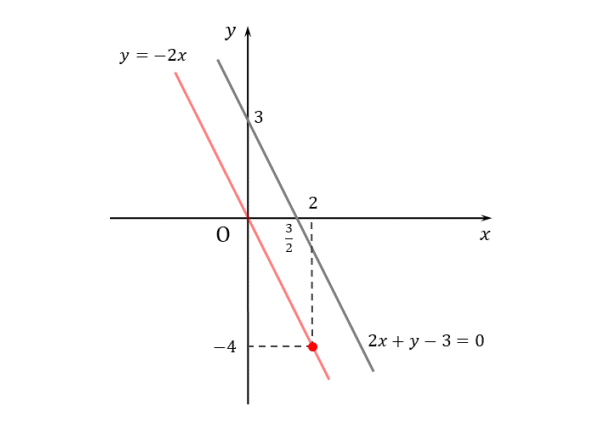
$(1) \quad$ 点 $(2 \ , \ -4)$ を通り、直線 $2x+y-3=0$ に平行な直線
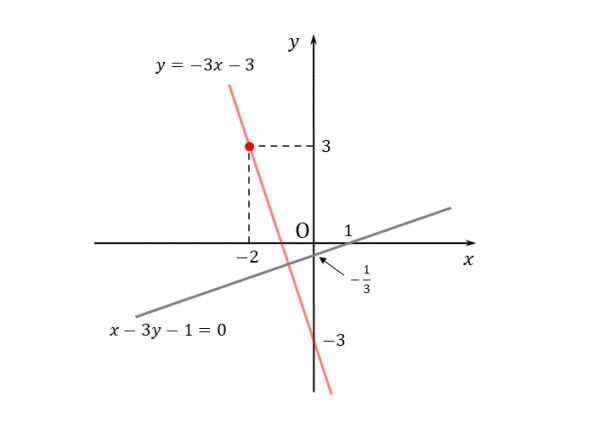
$(2) \quad$ 点 $(-2 \ , \ 3)$ を通り、直線 $x-3y-1=0$ に垂直な直線
例題(1)の解答・解説
例題(1)
次の直線の方程式を求めよ。
点 $(2 \ , \ -4)$ を通り、直線 $2x+y-3=0$ に平行な直線
文字x,yの項の係数がともに0ではないので、軸に垂直な直線ではありません。ですから、係数の吟味なしに変形して傾きを求めることができます。
与えられた直線の方程式を傾きが分かるように変形します。
例題(1)の解答例 1⃣
\begin{align*} \quad 2x+y-3=0 \end{align*}与えられた直線の方程式を変形すると
\begin{align*} \quad y=-2x+3 \end{align*}より、この直線の傾きは $-2$ である。
解答例の途中ですが、図示すると以下のようになります。本来であれば、問題文を読みながら作図します。方針を決めやすいので、作図の習慣をつけましょう。
求めたいのは与えられた直線に平行な直線の方程式です。2直線の平行条件を利用して傾きを求めます。
また、この直線は特定の点を通ります。傾きと1点の座標を用いて、直線の方程式を求めます。
例題(1)の解答例 2⃣
\begin{align*} \quad \vdots \end{align*}より、この直線の傾きは $-2$ である。
また、求める直線は点 $(2 \ , \ -4)$ を通る。
よって、求める直線の方程式は
\begin{align*} \quad y-\left( -4 \right)=-2 \left(x-2 \right) \end{align*}すなわち
\begin{align*} \quad y=-2x \end{align*}特に難しい計算はありません。yの係数に文字が含まれているかどうかの確認を忘れないようにしましょう。
例題(2)の解答・解説
例題(2)
次の直線の方程式を求めよ。
点 $(-2 \ , \ 3)$ を通り、直線 $x-3y-1=0$ に垂直な直線
例題(1)と同じ要領で解きます。文字x,yの項の係数がともに0ではないので、軸に垂直な直線ではありません。ですから、係数の吟味なしに変形して傾きを求めることができます。
与えられた直線の方程式を傾きが分かるように変形します。
例題(2)の解答例 1⃣
\begin{align*} \quad x-3y-1=0 \end{align*}与えられた直線の方程式を変形すると
\begin{align*} \quad y=\frac{1}{3} x-\frac{1}{3} \end{align*}より、この直線の傾きは $\frac{1}{3}$ である。
求めたいのは与えられた直線に垂直な直線の方程式です。2直線の垂直条件を利用して傾きを求めます。
例題(2)の解答例 2⃣
\begin{align*} \quad \vdots \end{align*}より、この直線の傾きは $\frac{1}{3}$ である。
この直線に垂直な直線の傾きを $m$ とすると
\begin{align*} \quad m \cdot \frac{1}{3}=-1 \end{align*}これを解くと
\begin{align*} \quad m=-3 \end{align*}解答例の途中ですが、求める直線を作図すると以下の通りです。
求める直線は特定の点を通ります。傾きが分かったので、傾きと1点の座標を用いて、直線の方程式を求めます。
例題(2)の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad m=-3 \end{align*}また、求める直線は点 $(-2 \ , \ 3)$ を通る。
よって、求める直線の方程式は
\begin{align*} \quad y-3=-3 \left\{x-\left(-2 \right) \right\} \end{align*}すなわち
\begin{align*} \quad y=-3x-3 \end{align*}例題(2)も特に難しくありません。与式を変形して傾きを利用できるので、易しい部類の問題です。
例題についてもう少し掘り下げてみましょう。基本的な解法はもちろんですが、この後に紹介する別解も大切です。