2次関数|2次関数の最大値や最小値について

2次関数の最大値や最小値について学習しましょう。
特に、今回は「2次関数のグラフの位置が定まらないとき」の考え方について確認します。どこに注目すれば良いのかを把握しましょう。
最大値や最小値に関する問題は、関数を扱った問題の中でも頻出です。それだけでなく、3次関数や指数・対数関数などにも大きな影響を与えるので大切な単元です。
この単元を苦手にしている人は意外と多いので、理解できるとかなり有利になります。
2次関数の最大値や最小値を考える前に知っておきたいこと
関数の最大値や最小値という場合、変数yの値の最大値や最小値のことを意味します。
これまで考えてきた2次関数では、変数xの値の取り得る範囲はすべての実数でした。この場合、2次関数の最大値や最小値は、頂点のy座標と等しくなります。
しかし、そうでない場合もあります。
定義域と値域の関係
変数xは、すべての実数ではなく、特定の範囲の値だけを取りうる場合があります。このような変数xの値の取りうる範囲のことを「定義域」と言います。
変数xに定義域が定められると、変数yは変数xの関数なので、変数yは特定の範囲の値しか取らなくなります。このようなyの値の取り得る範囲のことを「値域」と言います。
2次関数のグラフは放物線になる。したがって、グラフなしで考えると値域を間違う可能性が高くなる。関数を扱うときは、グラフを描く習慣を身に付けよう。
定義域や値域があると、2次関数の最大値や最小値は頂点のy座標と等しくならない場合があります。ですから、2次関数の最大値や最小値を考えるとき、変数xの定義域を考慮する必要があります。
変数yの値域は、変数xの定義域によって決まる。まずは変数xの定義域の方を意識しよう。
定義域や値域について復習しよう
定義域や値域に関する問題を解いてみましょう。
与式は1次関数の式です。1次関数のグラフは右上がり(または右下がり)の直線なので、比較的簡単に作図できます。
傾きが-2であるので、右下がりのグラフになります。
また、定義域(-1≦x≦3)が与えられているので、それに対応する値域があります。グラフを描いてみると分かりますが、直線ではなく線分になります。
右下がりのグラフで、定義域が-1≦x≦3であることから、x=-1のとき最大値をとり、x=3のとき最小値をとることが分かります。
復習問題のポイントと解答例は以下のようになります。なお、解答例では変数yの代わりにf(x)を用いています。
1次関数の値域を求める場合、計算だけで答えを求めてしまう人がいます。たしかに1次関数のグラフは直線になるので、作図なしでも値域を求めることは容易です。
しかし、計算だけで値域を求めてしまうのは、2次関数などの直線にならないグラフでは良い解き方とは言えません。入試レベルの問題になると、式に代入しただけで値域が得られるような問題は出題されないからです。
2次関数などの関数では、2つの変数x,yの関係を考えるのにグラフなしだとかなり難しくなる。しっかりとグラフを作図して考える習慣を身に付けておきたい。
2次関数の最大値や最小値
2次関数の最大値や最小値を考えるとき、1次関数のように単純ではありません。定義域の有無でグラフの形状が変わるからです。グラフを描いて考えるとよく分かります。
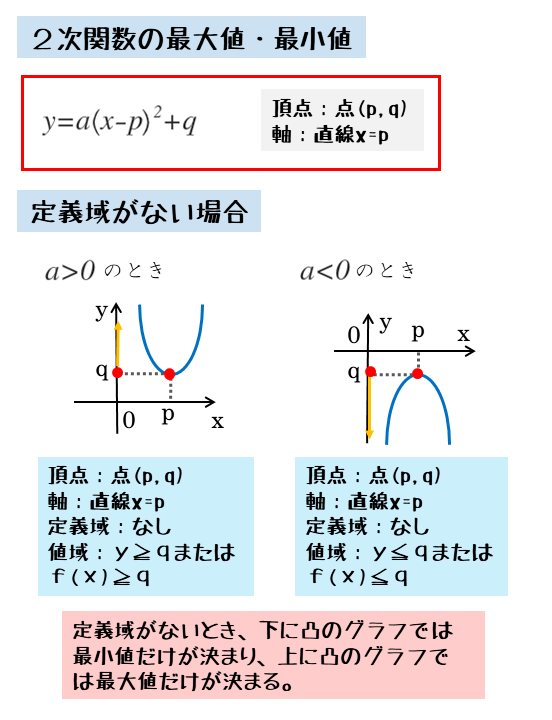
定義域がない場合
2次関数のグラフは放物線と呼ばれるグラフになります。対称の軸をもつ左右対称なグラフになるので、非常に分かりやすく特徴的な形状です。
このようなグラフを利用して、最大値や最小値をとる点を見つけられるようにしましょう。
2次関数のグラフの形状は、下に凸または上に凸の2パターンです。
変数xの定義域がない場合、つまり変数xがすべての実数をとる場合、最大値や最小値は以下のようになります。
下に凸の場合
- 最大値:なし
- 最小値:頂点のy座標
上に凸の場合
- 最大値:頂点のy座標
- 最小値:なし
グラフの形状から最大値や最小値が決まる。定義域がなければ、頂点のy座標が最大値または最小値。最大値か最小値のどちらかだけをとることにも注意しよう。
定義域がある場合
定義域がある場合でも、グラフの特徴を利用して2次関数の最大値や最小値を考えます。
定義域がある場合、それに対応する値域があります。グラフも定義域や値域に応じた部分だけになります。
定義域がある場合の最大値や最小値は、グラフの定義域に対する位置関係を決めてから考えます。ここで注意したいのは、定義域や軸の方程式に文字が含まれるかどうかです。
定義域や軸の方程式に文字が含まれなければ、グラフの定義域に対する位置は1つに定まるので、グラフが描ければ特に難しくありません。
問題は定義域や軸の方程式に文字が含まれるときです。このとき、グラフの定義域に対する位置は1つに定まりません。ですから、場合分けが必要になります。
グラフの位置は、軸の位置で決まります。ですから、場合分けのコツは軸と定義域との位置関係になります。
このようにグラフの定義域に対する位置を場合分けすることで、定義域内に残るグラフの形状を決めることができ、その結果、最大値や最小値を求めることができるようになります。
軸はx=~の方程式で表される直線。また、定義域は変数xの値の取りうる値の範囲。ともに変数xの値で表されるので、大小関係を比較することで場合分けすることができる。
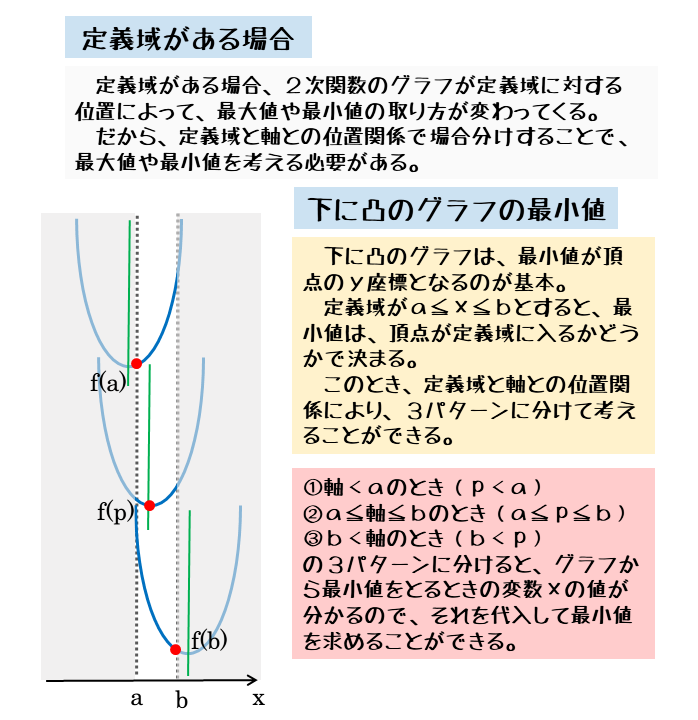
下に凸のグラフの場合の最小値
下に凸のグラフの場合を考えます。定義域がない場合の最大値や最小値は以下のようになりました。
下に凸のグラフ(定義域なし)
- 最大値:なし
- 最小値:頂点のy座標
まずはイメージしやすい最小値から考えます。下に凸のグラフで最小値を考えるときのポイントは「頂点が定義域に含まれるかどうか」です。
頂点の位置は軸の位置と連動しています。ですから、軸と定義域の位置関係で、頂点が定義域に含まれるかどうかを考えることができます。
頂点(=軸)と定義域の位置関係は3パターン(下に凸のグラフの最小値)
- (軸が定義域の左側)=(軸の値 < 定義域の左端の値)
- (軸が定義域内)=(定義域の左端の値 ≦ 軸の値 ≦ 定義域の右端の値)
- (軸が定義域の右側)=(定義域の右端の値< 軸の値)
軸と定義域の位置関係は3パターンあるので、それぞれの場合でグラフを書き分けてから最小値を考えます。
また、場合分けの条件は、軸の値と定義域の両端の値との大小関係から導出します。この条件は変数xについての不等式になります。
場合分けしてグラフを描くと、最小値を取る点が把握しやすくなります。最小値をとる点のx座標が分かったら、そのx座標を関数の式に代入してy座標を求めます。このy座標が関数の最小値になります。
最小値を取る点は、定義域の左端・頂点・定義域の右端のいずれかにできる。
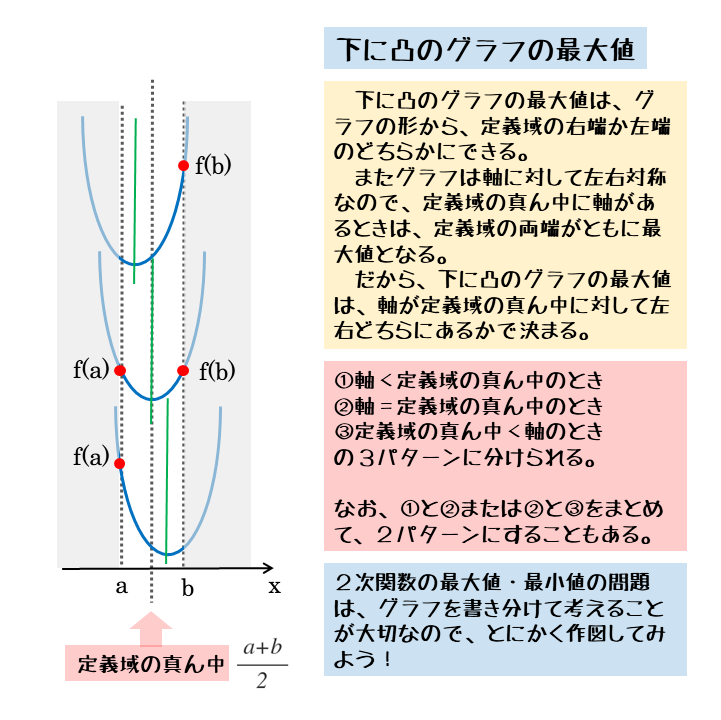
下に凸のグラフの場合の最大値
次は下に凸のグラフで最大値を考えます。下に凸のグラフでは、定義域がない場合、最大値はありませんでした。
定義域がある場合、最大値をとる点は、グラフの形状から定義域の左端または右端にできます。
基本的には最大値をとる点は1つですが、2つあるときもあります。それは、最大値を取る点がちょうど定義域の両端にできるときです。
このとき、軸は定義域の真ん中にあります。この状態から少しでもグラフが左右にずれると、最大値をとる点が定義域の左端か右端のいずれかにできます。
グラフが定義域に対して左右対称に残るのは、軸が定義域の真ん中にあるとき。
このことから、下に凸のグラフでの最大値は3パターンに場合分けできます。
頂点(=軸)と定義域の位置関係は3パターン(下に凸のグラフの最大値)
- (軸が定義域の真ん中より左側)=(軸の値 < 定義域の真ん中の値)
- (軸が定義域の真ん中にある)=(軸の値 = 定義域の真ん中の値)
- (軸が定義域の真ん中より右側)=(定義域の真ん中の値< 軸の値)
なお、2パターンで場合分けするときもあります。
頂点(=軸)と定義域の位置関係は3パターン(下に凸のグラフの最大値)
- (軸が定義域の真ん中より左側)=(軸の値 ≦ 定義域の真ん中の値)
- (軸が定義域の真ん中より右側)=(定義域の真ん中の値< 軸の値)
2パターンで場合分けでは、軸が定義域の真ん中にあるときを、左側になるときか右側になるときのどちらかに含めてしまいます。
最小値のときと同じように、軸と定義域の位置関係からグラフの位置が決まると、定義域内のグラフから最大値を取る点が分かります。
そして、その点のx座標と関数の式からy座標を求めれば、それが関数の最大値になります。
このように、軸や定義域に文字が含まれると、グラフの定義域に対する位置が1つに定まりません。グラフの位置が定まらないと、グラフが定義域内にどのように残るのかが分かりません。
定義域内でのグラフの形状が分からなければ、もちろん最大値や最小値をとる点も分かりません。
ですから、場合分けをして位置関係を自分で定める必要があります。
難しく感じるかもしれませんが、下に凸のグラフであれば、どんな式であっても上述の3パターンで場合分けします。ですから、グラフの描き分けができさえすれば、最大値や最小値を求めることは難しくありません。
上に凸のグラフの場合の最大値や最小値
定義域がない場合、上に凸のグラフでは最大値は頂点のy座標でした。つまり、最大値は頂点で決まります。
ですから、上に凸のグラフにおける最大値を求めるには、下に凸のグラフにおける最小値のときと同様の場合分けをします。
また、上に凸のグラフにおける最小値を求めるには、下に凸のグラフにおける最大値のときと同様の場合分けをします。凸の向きが逆になったので、場合分けも逆になります。
慣れるまでは下に凸のグラフで最大値や最小値を求めることができるようになろう。
難しく感じるかもしれませんが、そうでもありません。
軸の方程式や定義域が変わっても、グラフの定義域に対する位置関係は3パターンと決まっています。ですから、軸に値を入れずに3パターンのグラフを描く練習から始めると良いでしょう。
3パターンのグラフを描けるようになったら、グラフに値を追記していきましょう。値を追記できれば、場合分けの条件式を導出したり、最大値や最小値をとる点の座標を求めたりすることもできるようになります。
2次関数の最大値や最小値を求める流れをまとめると以下のようになります。
Recommended books
関数を上手に扱えるようになると、高校での数学はとてもラクになると思います。中学でも関数を扱いましたが、方程式や不等式との関係までは学習していません。
関数単体でなら何とかなっていても、方程式や不等式との関係性を理解しないと、高校では厳しくなります。逆に関係性が掴めれば、今までの苦労が何だったのかと思えるようになるでしょう。
関数は、たとえば物理の直線運動でもv-tグラフなどで登場するので、ぜひとも攻略しておきたい単元です。
オススメその1
1冊目に紹介するのは『おもしろいほどよくわかる高校数学 関数編』です。図解してあるので、関数に苦手意識がある人でも読みやすいでしょう。
高校数学で学ぶ2次関数・指数関数・対数関数・三角関数について、その関数が生まれた身近な現象から説明し、それぞれの関数の性質を考える過程に多くのページを割きました。
書籍の紹介にもあるように、身近な現象を例に挙げて話が進むので、イメージしやすいかと思います。興味のある人は一読してみてはいかがでしょうか。
オススメその2
2冊目に紹介するのは『改訂版 坂田アキラの2次関数が面白いほどわかる本』です。
『おもしろいほどよくわかる高校数学 関数編』は読み物に近いですが、こちらはより日常学習で利用しやすい教材です。
高校数学の基幹分野である「2次関数」は坂田の解説でマスターせよ!
累計50万部超の「坂田理系シリーズ」の「2次関数」。2009年4月に刊行した「新装版」の新課程版。学習者がつまずきやすい「場合分け」の丁寧な解説が最大の特長。基本から応用、重要公式からテクニックまで、幅広く網羅した「2次関数」対策の決定版!! 旧版になかった「解の配置」のテーマを増設。
教科書で理解できない箇所があっても本書が補助してくれるでしょう。そういう意味では基礎レベルなので、予習や復習のときに教科書とセットで利用するのが良いでしょう。
オススメその3
2次関数は、高校数学で学習する関数の中で最も基本的なものです。ですから、苦手意識をもたないようにしっかりと取り組んでおいた方が良いでしょう。
参考書や問題集を上手に利用しましょう。その他にも以下のような教材があります。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度、頭の中を整理しよう。
- 定義域は、変数xの取りうる値の範囲のこと。
- 値域は、変数yの取りうる値の範囲のこと。
- 定義域がある場合の最大値や最小値は、3パターンに場合分けして考える。
- まずは下に凸のグラフで最大値や最小値を求めることができるようになろう。