2次関数|関数について

「数と式」の単元が終わると、次の単元は「2次関数」です。「数と式」の単元では中学から橋渡しをしつつ、よく使われる数式について重点的に学習しました。
「2次関数」の単元でも同じように、中学の橋渡し的な事柄から徐々にメインに移っていきます。
2次関数という数式を扱う際には、「数と式」の単元で学習した事柄を利用します。消化不良だと式変形でつまづいてしまうので、忘れない程度に復習しておきましょう。
また、「2次関数」の単元は高校数学ではとても大切な単元です。基本的に関数が絡むと、この2次関数に帰着させることが多くなります。ですから、2次関数についての知識はたくさん持っていた方が良いでしょう。
そのような「2次関数」の単元ですが、まずは導入として中学で学習した関数を中心に学習しましょう。
関数の式とグラフ
関数の定義
関数とは、2つの変数x,yについて、xの値を決めるとyの値がただ1つに定まる関係にある数や、その関係を表した式のことです。
また、xの値を決めると、yの値がただ1つに定まるとき、「yはxの関数である」と言います。
変数として文字x,yを使うことが一般的ですが、特に決まっているわけではありません。とにかく2つの変数があり、一方の値が決まると他方の値がただ1つに決まるとき、関数の関係にあります。
変数とは、未知の数や不定の数などを表す文字のこと。普段使っている文字xなどは特定の値に定まらないので、変数と呼ぶこともある。また、物理では、速度vと時間tや、加速度aと時間tなどが関数の関係にある。
なお、これ以降は2つの変数をx,yの場合と考えて話を進めていきます。
2つの変数の関係を表すのが関数
関数であれば、2つの変数x,yの関係は式で表せます。関係を式で表せるので、ある変数xの値に対応する変数yの値を求めることができます。
また、「変数xの値が増加すると、変数yの値も増加する」というように、関数の式から変化の様子を調べることもできます。
このことから分かるのは、変数x,yの関係やその変化の様子はすべて関数の式で決まるということです。ですから、関数を扱うのであれば、変数x,yの関係やそれを表す式をつねに意識しておくことが大切です。
このような関数について、中学では「比例」「反比例」「1次関数」「2乗に比例する関数」を学習します。
関数を可視化したのがグラフ
2つの変数x、yの値は、関数の式で求めることができます。しかし、変数x,yの値の変化を知るには、値だけでは分かりにくいので、グラフを利用します。
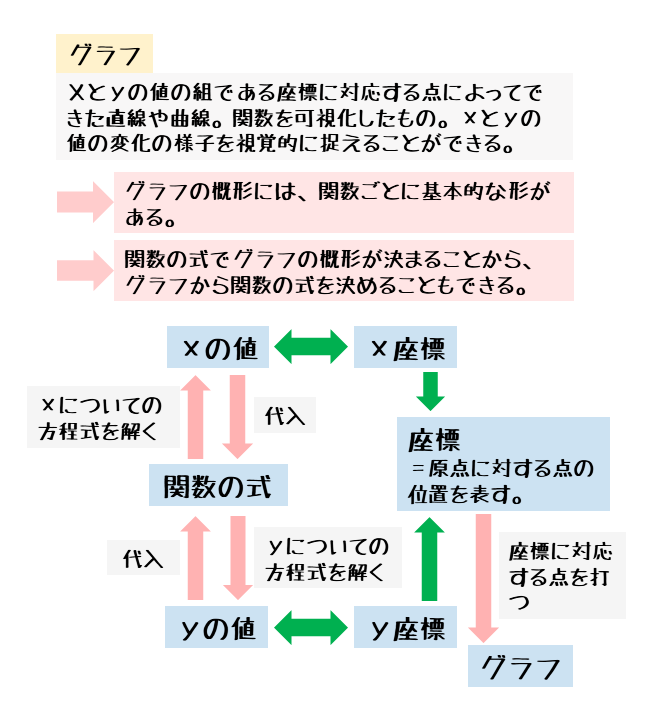
グラフで可視化するにあたって、変数xの値と、それによって定まる変数yの値を1つの組として扱います。これが座標です。
対応する変数x,yの組が座標。関数では、対応する変数x,yの値をセットで扱おう。
グラフを図示するとき、対応する変数x,yの値が座標となるような点を取ります。この点は、x軸やy軸などと名前の付いた数直線を直交させた座標平面の上に取ります。
関数の式から得られた座標を座標平面の上に取っていくと、グラフを描けます。グラフはたくさんの点が集まってできた直線や曲線のことです。
グラフは関数の式によって得られた変数x,yの値をもとにできている。
関数の式と座標との関係をまとめると以下のようになります。
関数の式とグラフの概形
このようにして得られるグラフは、関数の式によってその概形が決まっています。関数の式とグラフの概形をセットで覚えておきましょう。
グラフの概形
- 比例・1次関数 … 直線のグラフ
- 反比例 … 双曲線のグラフ
- 2乗に比例する関数 … 曲線または放物線のグラフ
関数では、変数x,yの値そのものだけなく、変数x,yの値の変化も考えることがあります。
この場合、値だけでは分かりにくいので、グラフを図示して考えます。ですから、関数のグラフの概形を覚えておいた方が良いでしょう。
関数の式と変数x,yの値との関係、そしてこれらとグラフとの関係をまとめると以下のようになります。
比例の式とグラフ
変数x,yがy=axという式で表される関係のとき、比例の関係にあると言います。
ここで、文字aは、変数ではなく定数で、比例定数と言います。関数ごとに固有の値が得られるからです。
また、比例の関係にあるとき、変数yは変数xの一次式で表され、定数項をもちません。
比例の関係にあるとき、グラフの概形や特徴をまとめると以下のようになります。
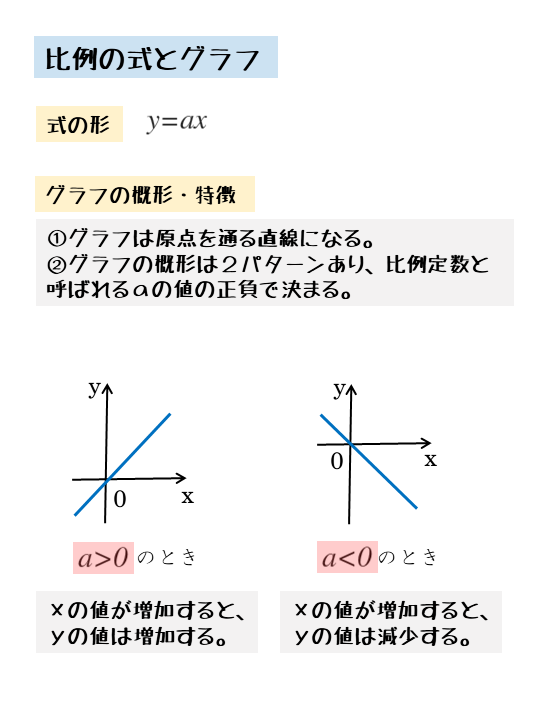
比例のグラフの概形と特徴
- 原点を通る直線
- 比例定数aの正負で右上がりか右下がりかが決まる
- a>0のとき、右上がりの直線
- a<0のとき、右下がりの直線
反比例の式とグラフ
変数x,yが、y=a/xという式で表される関係のとき、反比例の関係にあると言います。
文字aは、比例のときと同じく比例定数と言います。比例と同様に、関数ごとに固有の値が得られます。
反比例の関係を式から分かるように、変数yは変数xを分母にもつ分数で表されます。ですから、変数xが分母にあるので、x=0のとき 変数yの値は存在しません。
反比例の関係にあるとき、グラフの概形や特徴をまとめると以下のようになります。
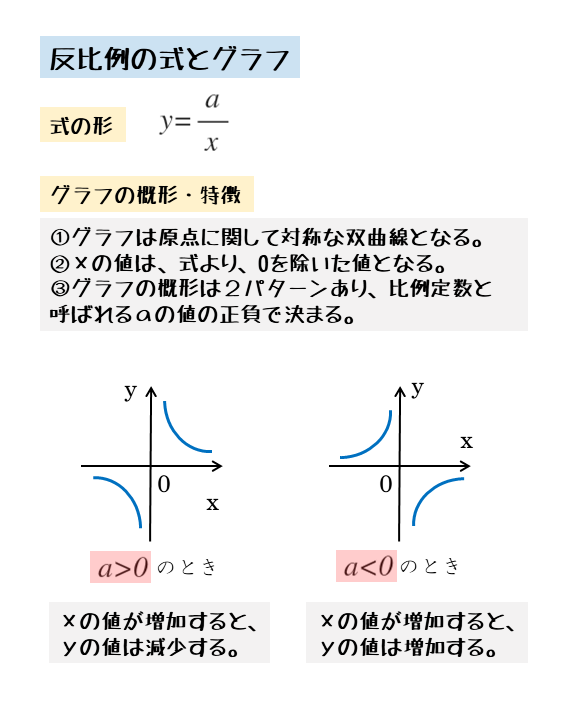
反比例のグラフの概形と特徴
- x=0のとき、 変数yの値は存在しない
- 双曲線と呼ばれる一対の曲線になる
- 双曲線の描き方は比例定数aの正負で2パターン(図参照)
反比例の関係では、変数x,yの値は、関数の式からxy=aを満たす関係にあります。この関係を上手に使うと、点の座標を求めやすくなります。
次は、1次関数や2乗に比例する関数についてです。