整数の性質|最大公約数と最小公倍数について

今回は最大公約数と最小公倍数について学習しましょう。こちらも小中学校で学習した内容の続きになるので、忘れていないか確認しながら取り組みましょう。
最大公約数と最小公倍数、互いに素
この単元では、以下のような事柄を学習します。
「最大公約数と最小公倍数について」で学習する事柄
- 最大公約数
- 最小公倍数
- 互いに素
- 2つの整数の積、最大公約数、最小公倍数の関係
初めて聞く用語があるので、定義を文言通り正しく覚えましょう。
最大公約数と最小公倍数
最大公約数
2つ以上の整数について、共通の約数のことを公約数と言います。公約数は、整数を積の形で表したときの共通な因数と考えることもできます。
このような公約数のうち、正で最大のものを最大公約数(Greatest Common Measure , G.C.M.)と言います。
12と16の最大公約数
それぞれの約数を調べると
\begin{align*} &\quad 12 \ \cdots \ 1 \ , \ 2 \ , \ 3 \ , \ \underline{4} \ , \ 6 \ , \ 12 \\[ 7pt ] &\quad 16 \ \cdots \ 1 \ , \ 2 \ , \ \underline{4} \ , \ 8 \ , \ 16 \end{align*}よって、$12$ と $16$ の最大公約数は $4$
教科書や参考書では、省略形はG.C.M.と記述されることが多いですが、他にも「G.C.D.(Greatest Common Divisor)」「G.C.F.(Greatest Common Factor)」「H.C.F.(Highest Common Factor)」等と記述されることもあるようです。
最小公倍数
2つ以上の整数について、共通の倍数のことを公倍数と言います。このような公倍数のうち、正で最小のものを最小公倍数(Least Common Multiple , L.C.M.)と言います。
12と16の最小公倍数
それぞれの倍数を調べると
\begin{align*} &\quad 12 \ \cdots \ 12 \ , \ 24 \ , \ 36 \ , \ \underline{48} \ ,\cdots \\[ 7pt ] &\quad 16 \ \cdots \ 16 \ , \ 32 \ , \ \underline{48} \ , \ 64 \ ,\cdots \end{align*}よって、$12$ と $16$ の最小公倍数は $48$
教科書や参考書では、省略形はL.C.M.と記述されることが多いですが、小文字にしたlcmと記述されることもあります。
最大公約数や最小公倍数の求め方その1
中学までの求め方(2つの整数のとき)
整数がそれほど大きくなければ、暗算で最大公約数や最小公倍数を求めることができるでしょう。
たとえば、24と36の最大公約数や最小公倍数であれば、頭の中では次のようなことを考えているのではないでしょうか。
24と36の最大公約数と最小公倍数
それぞれの約数を大きい方から調べると
\begin{align*} &\quad 36 \ \cdots \ 36 \ , \ 18 \ , \ \underline{12} \ ,\cdots \\[ 7pt ] &\quad 24 \ \cdots \ 24 \ , \ \underline{12} \ ,\cdots \end{align*}よって、$24$ と $36$ の最大公約数は $12$
また、それぞれの倍数を小さい方から調べると
\begin{align*} &\quad 36 \ \cdots \ 36 \ , \ \underline{72} \ , \ 108 \ ,\cdots \\[ 7pt ] &\quad 24 \ \cdots \ 24 \ , \ 48 \ , \ \underline{72} \ ,\cdots \end{align*}よって、$24$ と $36$ の最小公倍数は $72$
最大公約数であれば、大きい方の整数の約数を大きい順に挙げながら、その約数で小さい方の整数を割り切れるか調べましょう。
例のように、36の約数を大きい方から挙げ、それで24を割ります。割り切れれば、それは24の約数でもあります。36や18では割り切れませんが、12なら割り切れます。
また、最小公倍数であれば、大きい方の整数の倍数を小さい順に挙げながら、それが小さい方の整数で割り切れるかを調べましょう。
例のように、36の倍数を小さい方から挙げ、それを24で割ります。割り切れれば、それは24の倍数でもあります。36は24で割り切れませんが、72なら24で割り切れます。
2つの整数がそれほど大きくなければ、このような調べ方もあります。暗算でできるのが利点ですが、難しく感じるならば、きちんと書き並べる方法が最も確実です。
書き並べる方法よりも手間の少ない方法が筆算です。
筆算では、2つの整数を共通に割り算するのが特徴的です。割り算は下にしていくので、商を2つの整数の下にそれぞれ書きます。これを繰り返し、共通に割れなくなれば筆算を終えます。
共通に割れなくなれば、縦と横に並んだ数を使って、最大公約数や最小公倍数を求めます。求め方は簡単です。
筆算での求め方
- 最大公約数 … 縦に並んだ数の積
- 最小公倍数 … 縦と横に並んだ数の積
この方法では、手順通りに進めていけば機械的に求めることができます。
中学までの求め方(3つの整数のとき)
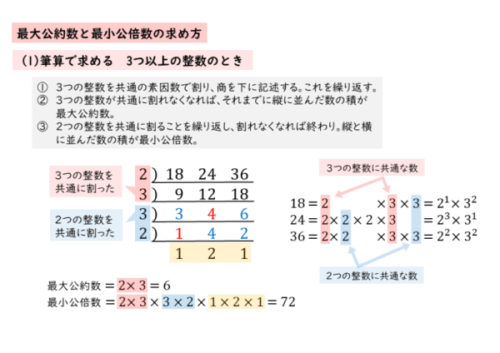
3つ以上の整数の場合、少し難しくなります。3つの整数を共通に割っていき、商を下にそれぞれ書いていくことを繰り返します。ここまでは同じですが、共通に割れなくなった後が問題です。
3つの整数を共通に割れなくなったら、それまでに縦に並んだ数の積が最大公約数になります。ここから先は最小公倍数を求めるための計算です。
3つの整数のうち、2つを共通に割っていきます。このとき、割れない残りの1つはそのまま下に書きます。2つの整数でも共通に割れなくなれば筆算を終えます。縦と横に並んだ数の積が最小公倍数です。
3つ以上の整数では、最小公倍数の求め方に注意する必要があります。ここまでが小・中学校で学習した方法です。