複素数と方程式｜高次式の因数分解について

数学２

今回は、高次式の因数分解について学習しましょう。ここで扱う整式は高次式です。ですから、展開や因数分解の公式をすぐには利用して因数分解することができません。

剰余の定理も関わるので、覚えていない人は確認しておきましょう。

高次式の因数分解

高次式とは、その名の通り次数の高い整式のことです。高次式という場合、一般に、３次以上の次数をもつ整式のことを指します。

このような高次式を因数分解する問題では、そのほとんどで２次式や３次式の展開や因数分解で学習した公式が役に立ちません。ですから、別の手段を用いて因数分解します。

因数定理

前の単元で、剰余の定理について学習しました。

剰余の定理

\begin{align*} &\text{1⃣ 整式 $P(x)$ を1次式 $x-k$ で割ったときの余りは} \\[ 5pt ] &\quad P(k) \quad \text{（剰余の定理）} \\[ 10pt ] &\text{2⃣ 整式 $P(x)$ を1次式 $ax+b$ で割ったときの余りは} \\[ 5pt ] &\quad P \left(-\frac{b}{a} \right) \end{align*}

剰余の定理では、余りが出るのが基本ですが、実際には余りが０、つまり割り切れることもあるはずです。

このような場合、整式は割る式と商との積の形で表されます。このとき、割る式である１次式は、整式の因数となります。

これが因数定理です。因数定理は、剰余の定理において、特に余りが０となるときの定理です。

因数定理

\begin{align*} &\text{1⃣ $1$ 次式 $x-k$ が整式 $P(x)$ の因数である。} \\[ 5pt ] &\quad \Leftrightarrow \ P(k)=0 \quad \text{（因数定理）} \\[ 10pt ] &\text{2⃣ $1$ 次式 $ax+b$ が整式 $P(x)$ の因数である。} \\[ 5pt ] &\quad \Leftrightarrow \ P \left(-\frac{b}{a} \right)=0 \end{align*}

剰余の定理を利用して、整式を１次式で割ったときの余りを調べます。このとき、余りが０となれば、因数定理が成り立つので、整式は１次式を因数にもつことが分かります。

因数となる１次式が分かれば、その１次式で整式を割り算することができます。そして、商からその他の因数を知ることができます。

高次式の因数を調べてみよう

次の例題を考えてみましょう。

例題１

\begin{align*} &\text{次の整式は $[ \ ]$ 内の $1$ 次式を因数にもつことを示せ。} \\[ 5pt ] &(1) \quad 2x^{\scriptsize{3}}+3x^{\scriptsize{2}}-11x-6 \quad [ x-2 ] \\[ 7pt ] &(2) \quad 6x^{\scriptsize{3}}-13x^{\scriptsize{2}}-14x-3 \quad [ 2x+1 ] \end{align*}

例題１(1)の解答・解説

例題１(1)

\begin{align*} &\text{次の整式は $[ \ ]$ 内の $1$ 次式を因数にもつことを示せ。} \\[ 5pt ] &\quad 2x^{\scriptsize{3}}+3x^{\scriptsize{2}}-11x-6 \quad [ x-2 ] \end{align*}

与式を１次式ｘ－２で割り算して余りを調べます。このとき、筆算するのではなく、剰余の定理を利用します。剰余の定理を利用すれば、式の値から余りを調べることができます。

例題１(1)の解答例

\begin{align*} &\quad P(x)=2x^{\scriptsize{3}}+3x^{\scriptsize{2}}-11x-6 \\[ 7pt ] &\text{とおく。} \\[ 5pt ] &\text{与式を $x-2$ で割ったときの余りは} \\[ 5pt ] &\text{剰余の定理より} \\[ 5pt ] &\quad P(2)=2 \cdot 2^{\scriptsize{3}}+3 \cdot 2^{\scriptsize{2}}-11 \cdot 2-6 \\[ 7pt ] &\text{整理すると} \\[ 5pt ] &\quad P(2)=0 \\[ 7pt ] &\text{よって、因数定理より、与式は} \\[ 5pt ] &\text{$x-2$ を因数にもつ。} \end{align*}

与式にｘ＝２を代入して、式の値を求めます。このときの値が、与式をｘ－２で割った余りに等しくなります。式の値が０となったので、余りは０です。

この結果から因数定理が成り立つので、与式は１次式ｘ－２を因数にもちます。

例題１(2)の解答・解説

例題１(2)

\begin{align*} &\text{次の整式は $[ \ ]$ 内の $1$ 次式を因数にもつことを示せ。} \\[ 5pt ] &\quad 6x^{\scriptsize{3}}-13x^{\scriptsize{2}}-14x-3 \quad [ 2x+1 ] \end{align*}

例題1(1)と同じ要領で解きます。

例題１(2)の解答例

\begin{align*} &\quad P(x)=6x^{\scriptsize{3}}-13x^{\scriptsize{2}}-14x-3 \\[ 7pt ] &\text{とおく。} \\[ 5pt ] &\text{与式を $2x+1$ で割ったときの余りは} \\[ 5pt ] &\text{剰余の定理より} \\[ 5pt ] &\quad P\left(-\frac{1}{2} \right)=6 \cdot \left(-\frac{1}{2} \right)^{\scriptsize{3}}-13 \cdot \left(-\frac{1}{2} \right)^{\scriptsize{2}}-14 \cdot \left(-\frac{1}{2} \right)-3 \\[ 7pt ] &\text{整理すると} \\[ 5pt ] &\quad P\left(-\frac{1}{2} \right)=0 \\[ 7pt ] &\text{よって、因数定理より、与式は} \\[ 5pt ] &\text{$2x+1$ を因数にもつ。} \end{align*}

剰余の定理を利用すれば、整式を１次式で割った余りを調べることができます。余りから因数定理が成り立てば、整式の因数を知ることができます。

高次式の因数分解では、剰余の定理と因数定理を突破口にして解いていきます。

組立除法

整式の因数のうち１つでも分かれば、残りの因数を知ることができます。

残りの因数を調べるとき、一般に、因数である１次式を割る式として割り算します。整式の割り算を行うわけですが、意外と計算ミスをしやすいので注意が必要です。

割る式が１次式のとき限定になりますが、筆算するよりも簡単に計算する方法があります。その計算方法が組立除法です。

組立除法は余りの有無によらず使えるので、割る式が１次式のときであれば積極的に利用しましょう。

割る式が１次式であれば組立除法。

組立除法の仕組み

組立除法は以下のような方法です。

組立除法

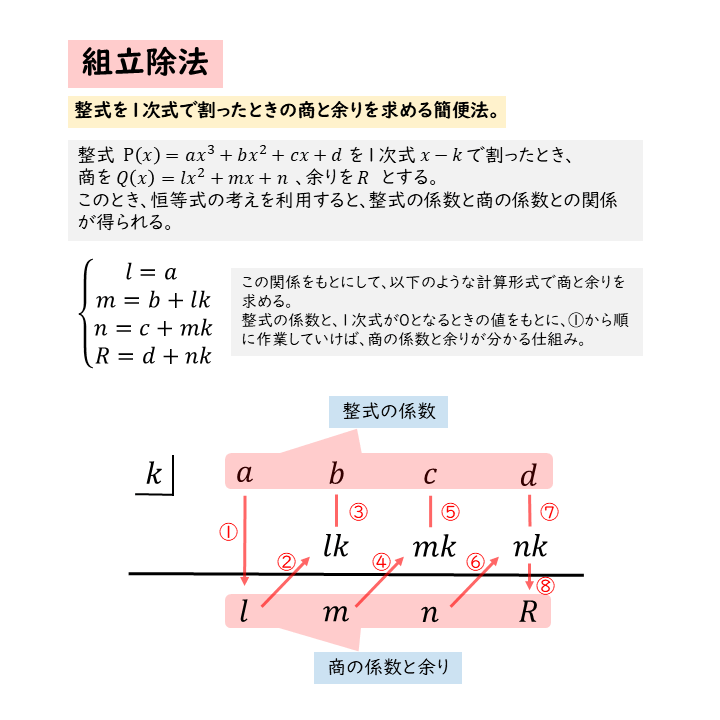
整式Ｐ(ｘ)を１次式ｘ－ｋで割ったときの商Ｑ(ｘ)と余りＲを求める簡便法。

組立除法の仕組みは、恒等式の考えがもとになっています。以下の説明では、整式は３次式としますが、一般の整式であれば同様のことが成り立ちます。

組立除法の仕組み 1⃣

\begin{align*} &\quad P(x)=ax^{\scriptsize{3}}+bx^{\scriptsize{2}}+cx+d \\[ 7pt ] &\text{を $x-k$ で割ったときの商を} \\[ 5pt ] &\quad Q(x)=lx^{\scriptsize{2}}+mx+n \\[ 7pt ] &\text{とし、余りを $R$ とすると} \\[ 5pt ] &\quad P(x)=\left(x-k \right) Q(x)+R \\[ 7pt ] &\text{と表せる。} \\[ 5pt ] &\text{このとき、$l \ , \ m \ , \ n \ , \ R$ を恒等式を利用して表す。} \end{align*}

商や余りを定義すれば、割り算の基本公式を用いて、もとの整式を表すことができます。

さらに、この等式について係数比較すると、商の係数や余りをもとの整式の係数で表すことができます。

組立除法の仕組み 2⃣

\begin{align*} &\quad \vdots \\[ 5pt ] &\quad ax^{\scriptsize{3}}+bx^{\scriptsize{2}}+cx+d=\left(x-k \right)\left(lx^{\scriptsize{2}}+mx+n \right)+R \\[ 7pt ] &\text{右辺を整理すると} \\[ 5pt ] &\quad ax^{\scriptsize{3}}+bx^{\scriptsize{2}}+cx+d=lx^{\scriptsize{3}}+\left(-lk+m \right)x^{\scriptsize{2}}+\left(-mk+n \right)x+\left(-nk+R \right) \\[ 7pt ] &\text{両辺の係数を比較すると} \\[ 5pt ] &\left\{ \begin{array}{l} a=l \\ b=-lk+m \\ c=-mk+n \\ d=-nk+R \end{array} \right. \\[ 7pt ] &\text{よって} \\[ 5pt ] &\left\{ \begin{array}{l} l=a \\ m=b+lk \\ n=c+mk \\ R=d+nk \end{array} \right. \end{align*}

商の係数や余りが、もとの整式の係数を用いて表されていることが分かります。

整式の係数は初めから分かっています。ですから、上述の４つの関係式を用いれば、商の係数を次数の高い方から順に求めることができます。そして、商の係数だけでなく、余りを求めることもできます。

ただ、４つの関係式を覚えるのは面倒です。商の係数や余りを機械的に求める方法が組立除法です。組立除法では、数の配置の仕方や数の書き込む順番が決まっています。

組立除法の仕組み
組立除法は機械的に割り算する方法

図示したような計算形式で商（厳密には商の係数）と余りを求めます。例題を用いて手順を確認しましょう。

組立除法を扱った例題

次の例題を考えてみましょう。

例題２

\begin{align*} &\text{組立除法を用いて、商と余りを求めよ。} \\[ 5pt ] &(1) \quad \left(x^{\scriptsize{3}}-10x+2 \right) \div \left(x+2 \right) \\[ 7pt ] &(2) \quad \left(8x^{\scriptsize{3}}-2x^{\scriptsize{2}}-7x+6 \right) \div \left(4x-3 \right) \end{align*}

例題2(1)の解答・解説

例題２(1)

\begin{align*} &\text{組立除法を用いて、商と余りを求めよ。} \\[ 5pt ] &\quad \left(x^{\scriptsize{3}}-10x+2 \right) \div \left(x+2 \right) \end{align*}

余りだけであれば、剰余の定理を利用して求めることができます。しかし、商を求める必要があるので、本来なら筆算で求めるのが基本的な解法です。

ここでは、割る式が１次式であることに注目します。問題で指示されていますが、割る式が１次式であれば組立除法を用います。

組立除法を用いると、以下のようになります。割られる整式には２次の項がないので、その係数は０とします。組立除法の手順は以下の通りです。

組立除法による整式の割り算(1)
例題２(1)の組立除法

例題２(1)の解答例

\begin{align*} &\left\{ \begin{array}{l} l=a \\ m=b+lk \\ n=c+mk \\ R=d+nk \end{array} \right. \end{align*}

上記の関係に合わせて計算していく。

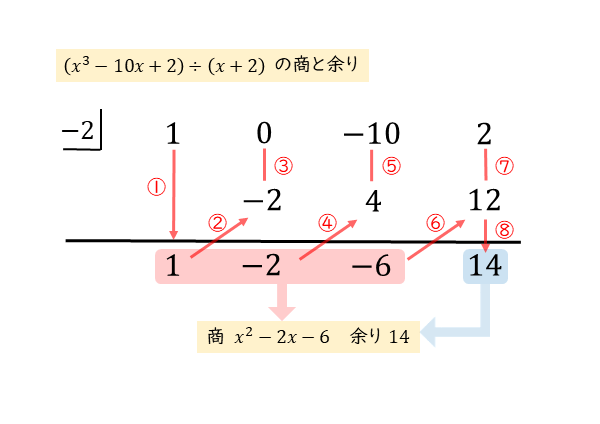
(1) １行目に、割られる式 $x^{\scriptsize{3}}-10x+2$ の係数 $1 \ , \ 0 \ , \ -10 \ , \ 2$ と、割る式 $x+2=x-(-2)$ の $-2$ を書く。$-2$ はＬ字で囲んでおく。

(2) 最初の $1$ はそのまま下に下して $1$ と書く。（図①）

(3) 次に $(-2) \times 1=-2$ を $0$ の下に書き、$0+(-2)=-2$ を下に書く。（図②，③）

(4) さらに $(-2) \times (-2)=4$ を $-10$ の下に書き、$-10+4=-6$ を下に書く。（図④，⑤）

(5) $(-2) \times (-6)=12$ を $2$ の下に書き、$2+12=14$ を下に書く。（図⑥，⑦，⑧）

横線の下に並んだ数が、商の係数と余り。

よって、商 $x^{\scriptsize{2}}-2x-6$、余り$14$

割られる式が３次式です。これを１次式で割ると、商は２次式で、余りは定数です。

組立除法を利用できるのは、割る式が１次式のときだけです。整式の係数を抜き出して計算するので、筆算よりも計算ミスしにくいのが利点です。

また、「掛けて足す」の繰り返しの計算で済みます。筆算の「掛けて引く」と異なるので注意が必要ですが、とても簡単な計算方法です。

組立除法では「掛けて足す」の繰り返し。これまでの「掛けて引く」割り算とは異なるので注意しよう。

例題2(2)の解答・解説

例題２(2)

\begin{align*} &\text{組立除法を用いて、商と余りを求めよ。} \\[ 5pt ] &\quad \left(8x^{\scriptsize{3}}-2x^{\scriptsize{2}}-7x+6 \right) \div \left(4x-3 \right) \end{align*}

割る式が１次式であることを確認して、組立除法を用いて商と余りを求めます。

例題２(1)と同じ要領で解きたいのですが、割る式の１次の項の係数に注意しましょう。組立除法を用いた割り算では、割る１次式の係数は１であることが条件です。

組立除法の注意点

\begin{align*} &\text{与式を $4x-3$ で割ったときの商 $Q(x)$ と余り $R$ で表すと} \\[ 7pt ] &\quad 8x^{\scriptsize{3}}-2x^{\scriptsize{2}}-7x+6=\left(4x-3 \right)Q(x)+R \\[ 7pt ] &\text{組立除法では割る $1$ 次式の係数が $1$ であるので} \\[ 7pt ] &\quad 8x^{\scriptsize{3}}-2x^{\scriptsize{2}}-7x+6=\left(x-\frac{3}{4} \right) \cdot \underline{4Q(x)}+R \\[ 7pt ] &\text{つまり、組立除法で得られる商は $4Q(x)$ となる。} \\[ 5pt ] &\text{よって、組立除法の後に $4$ で割って、商 $Q(x)$ を求める。} \end{align*}

割る１次式の係数が１でないときは、商に注意しましょう。組立除法の手順は以下の通りです。

組立除法による整式の割り算(2)

例題２(2)の解答例

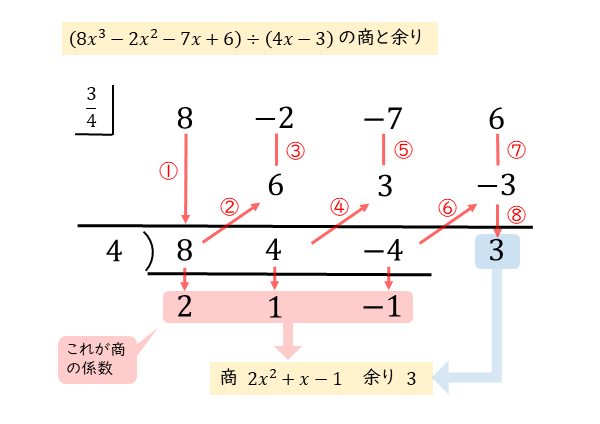
(1) まず、１行目に、割られる式 $8x^{\scriptsize{3}}-2x^{\scriptsize{2}}-7x+6$ の係数 $8 \ , \ -2 \ , \ -7 \ , \ 6$ と割る式 $4x-3=4 \left(x-\frac{3}{4} \right)$ の $\frac{3}{4}$ を書く。$\frac{3}{4}$ はＬ字で囲んでおく。

(2) 最初の $8$ はそのまま下に下して $8$ と書く。（図①）

(3) 次に $\frac{3}{4} \times 8=6$ を $-2$ の下に書き、$-2+6=4$ を下に書く。（図②，③）

(4) さらに $\frac{3}{4} \times 4=3$ を $-7$ の下に書き、$-7+3=-4$ を下に書く。（図④，⑤）

(5) $\frac{3}{4} \times (-4)=-3$ を $6$ の下に書き、$6+(-3)=3$ を下に書く。（図⑥，⑦，⑧）

(6) 得られた商をさらに $4$ で割った $2 \ , \ 1 \ , \ -1$ が、本当に求めたい商の係数。

よって、商 $2x^{\scriptsize{2}}+x-1$、余り$3$

組立除法で得られた商（の係数）を４で割ります（手順(6)）。この手順を忘れたり、余りを割ったりしないように気を付けましょう。

割る１次式の係数が１でないときは要注意。

高次式の因数分解の手順

高次式を因数分解するとき、剰余の定理や因数定理、そして組立除法を利用します。どのような手順で進めていくのかを整理しておきましょう。

高次方程式の因数分解の手順

  1. Ｐ(ｋ)＝０となるｋを見つける。（剰余の定理の利用）
  2. ｋが見つかれば、因数定理が成り立つ１次式が分かる。
  3. この１次式を割る式として、組立除法で割り算する。

剰余の定理や因数定理、組立除法を適切に利用するために、それらがどんなものなのかを把握しておくことが大切です。単なる用語の暗記で済ませないようにしましょう。教科書や参考書で過程を何度も読み返し、きちんと理解しておきましょう。

公式や定理を適切に利用するには、それらが導出される過程を理解することが大切。結果よりも過程を重視しよう。この姿勢はすべての科目に共通する。

次は、高次式の因数分解を扱った問題を実際に解いてみましょう。

数学２因数分解,複素数と方程式,因数定理,組立除法,高次式

Posted by kiri