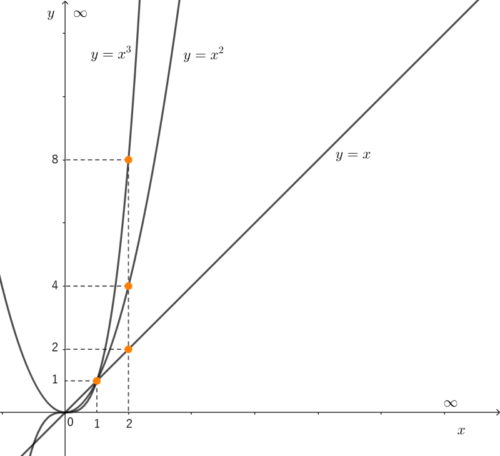数列の極限｜無限大にも程度の違いがある

07/09/2021数学３

今回は数学３「数列の極限」の発散の程度について学習しましょう。数列の極限とは直接関係ありませんが、気分転換に読むと良いでしょう。

極限を取ったとき、無限大に発散する場合は色々あります。どれも発散するのは同じですが、はたして発散の程度も同じなのでしょうか。

1. 無限大に発散する例
2. 無限大の程度の違いを知ろう
3. 無限大の程度の違いを利用しよう
4. さいごに
5. Recommended books

無限大に発散する例

ｎ，ｎ²，ｎ³を例に考えてみましょう。

例１

\begin{align*} &\quad n \to \infty \quad \cdots \text{①} \\[ 7pt ] &\text{のとき} \\[ 5pt ] &\quad n^{\scriptsize{2}} \to \infty \quad \cdots \text{②} \\[ 7pt ] &\quad n^{\scriptsize{3}} \to \infty \quad \cdots \text{③} \end{align*}

①～③はどれも無限大に発散しています。しかし、発散の程度は同じではありません。これはグラフを見るとよく分かります。

同じｘに対するｙの値の移り変わりに違いがあります。累乗の指数が大きくなるにつれて、その値も飛躍的に大きくなります。

また、①～③のことを言葉で言うとすれば、以下のように、異なる言い回しになります。

発散の程度を言葉で言い表す

ｎと同じくらいの∞を１次の無限大
ｎ²と同じくらいの∞を２次の無限大
ｎ³と同じくらいの∞を３次の無限大

同じ無限大の記号∞を使っていますが、言葉にすれば無限大の程度が異なることが分かります。

無限大の程度の違いを知ろう

無限大の程度が違うことをもっと体感するために、次の極限を考えてみましょう。

例２

\begin{align*} &\displaystyle \lim_{n \to \infty} {\frac{n^{\scriptsize{3}}}{n^{\scriptsize{2}}} } \quad \cdots \text{④} \\[ 10pt ] &\displaystyle \lim_{n \to \infty} {\frac{n^{\scriptsize{2}}}{n^{\scriptsize{3}}} } \quad \cdots \text{⑤} \end{align*}

まず、④式の極限を求めます。

④式の極限

\begin{align*} \displaystyle \lim_{n \to \infty} {\frac{n^{\scriptsize{3}}}{n^{\scriptsize{2}}} } &= \displaystyle \lim_{n \to \infty} n \\[ 10pt ] &= \infty \end{align*}

次に、⑤式の極限を求めます。

⑤式の極限

\begin{align*} \displaystyle \lim_{n \to \infty} {\frac{n^{\scriptsize{2}}}{n^{\scriptsize{3}}} } &= \displaystyle \lim_{n \to \infty} {\frac{1}{n} } \\[ 10pt ] &= 0 \end{align*}

④，⑤式はともに分母と分子が無限大に発散する不定形です。

不定形ではありますが、実際に極限をとると、一方は無限大に発散し、他方は０に収束します。これは、無限大に程度の違いがあり、ｎ³ の方がｎ²よりも速く無限大になることを示しています。

不定形

\begin{align*} &\quad \frac{\infty}{\infty} \ , \ \infty – \infty \\[ 7pt ] &\text{の形になるものを不定形という。} \end{align*}

無限大の程度の違いを利用しよう

このように同じ無限大に発散するとしても、発散の程度に違いがあることを知っていると、極限値の予想や確認を簡単に行うこともできます。

発散の程度の違いを利用した例

\begin{align*} &\quad \displaystyle \lim_{n \to \infty} {\frac{n^{\scriptsize{2}}-n+2}{2n^{\scriptsize{2}}+3} } \\[ 10pt ] &\text{について、分母、分子の $1$ 次の項と} \\[ 5pt ] &\text{定数項を無視して} \\[ 5pt ] &\quad \displaystyle \lim_{n \to \infty} {\frac{n^{\scriptsize{2}}-n+2}{2n^{\scriptsize{2}}+3} } \ \fallingdotseq \ \displaystyle \lim_{n \to \infty} {\frac{n^{\scriptsize{2}}}{2n^{\scriptsize{2}}} } \\[ 10pt ] &\text{と考えても、ともに同じ極限を得る} \\[ 5pt ] &\text{ことができる。} \end{align*}

１次の項や定数項は、２次の項に比べて無限大の程度が小さいと考えています。その考えをもとに、分母や分子にある１次の項や定数項を無視して、極限を求めます。

不要な項を無視したときの極限

\begin{align*} \displaystyle \lim_{n \to \infty} {\frac{n^{\scriptsize{2}}-n+2}{2n^{\scriptsize{2}}+3} } \ &\fallingdotseq \displaystyle \lim_{n \to \infty} {\frac{n^{\scriptsize{2}}}{2n^{\scriptsize{2}}} } \\[ 10pt ] &= \displaystyle \lim_{n \to \infty} {\frac{1}{2} } \\[ 10pt ] &= \frac{1}{2} \end{align*}

１次の項や定数項を省略せずに、もとの式から極限を求めます。

もとの式での極限

\begin{align*} \displaystyle \lim_{n \to \infty} {\frac{n^{\scriptsize{2}}-n+2}{2n^{\scriptsize{2}}+3} } &= \displaystyle \lim_{n \to \infty} {\cfrac{1-\cfrac{1}{n}+\cfrac{2}{n^{\scriptsize{2}}} }{ 2+\cfrac{3}{n^{\scriptsize{2}}} } } \\[ 10pt ] &= \frac{1}{2} \end{align*}

不要な項を無視しても、もとの式での極限と同じ結果になります。

なお、与式は∞/∞となる不定形ですが、分母と分子を分母の最高次の項で割るのは、無限大の程度の違いを考えているからです。

これまでは何となく式変形をしていたと思います。今後は、無限大の程度の違いを利用したものだと意識しながら式変形できるでしょう。

また、１次の項や定数項を無視するのは、乱暴な感じがするかもしれません。

しかし、もとの式での極限で分かるように、最高次である２次の項で割って極限を取れば、１次の項や定数項は０に収束します。最終的に０に収束することを知っているので、先に省略しても構わないことが分かります。

１次の項や定数項を省略するのは、無限大の程度の違いを知っているからできることです。

さいごに

極限を調べる問題では、以上のように無限大の程度の違いを考えて、極限値の予想や答えの確かめに利用することができます。無限大の程度に違いがあれば、不要な項を省略することもできます。

ただし、乱暴に感じたのは当然で、このことを利用するのは限定的にしておきましょう。便利ではありますが、あくまでも予想や確認にとどめておくことです。間違っても答案として記述しないように気を付けましょう。

極限の予想や確認に便利ではあるが、あくまでも簡易的な予想や確認に利用する程度にしておこう。

Recommended books

数列の極限を基本から学習できる書籍です。気になる書籍があったら、ぜひ一読してみて下さい。

オススメその１

『大学入試１０日で極める数列・数列の極限』は、理系の人向けの問題集です。出版年月日が新しいので、近年の出題傾向を踏まえた内容になっています。傾向と対策は基本なので、ありがたい一冊です。

短期間で基礎から難関大突破レベルまで効率的に学習できる、理系数学の分野別入試問題集。主要大学の入試において、近年出題率の高い分野の問題を掲載。補充問題も充実。

大学入試１０日で極める数列・数列の極限（理系のための分野別問題集）

created by Rinker

オススメその２

数学３の演習であれば、『数学３基礎問題精講』の１冊でほとんど足ります。

本書は教科書から入試への橋渡しをコンセプトにした入試対策書です。
数学３を１２５のテーマに分け、基礎問→精講→解答→ポイント→演習問題で１つのテーマを完結していますのでスムーズに無理なく学習ができます。
また、一つのテーマは１ページもしくは２ページの見開きになっています。旺文社ＨＰで、演習問題の解答をダウンロードできるようになりました。
旺文社公式サイト

難関大や医歯薬系であれば、『数学３標準問題精講』や『数学３上級問題精講』までやれば大丈夫でしょう。

数学３基礎問題精講

created by Rinker

数学３標準問題精講

created by Rinker

数学３上級問題精講

created by Rinker

以下、数学の読み物としてオススメです。あくまでも読み物なので、受験のためというよりも、教養を深めるために読むと良いでしょう。

オススメその３

『意味がわかれば数学の風景が見えてくる改訂合本』は、「数学の風景が見える」シリーズ４冊が１冊になった合本です。

計算ができるようになることよりも「意味がわかること」に焦点が当てられているので、丁寧な解説になっています。ページ数が多いのは丁寧に解説してあるからです。

多くの読者の声にお応えして「数学の風景が見える」シリーズ４冊を１冊にまとめました！
新規原稿を加えるなどして新しく生まれ変わった本書は、７００ページを超えるボリュームですが、わかりやすい文章と見開き完結のスタイルでスラスラ読めます。「微分積分」「数と計算」「図形空間」「統計確率」の４部構成で、どちらから読んでもＯＫ。
本書を読めば、数学が今までとは違ったものに見えてくるでしょう。

数学が苦手な原因は、数式が単なる数や文字の羅列にしか見えていないからではないでしょうか。もしそうであれば、立式したり、式変形したりするのはかなり苦労するでしょう。

そのことを踏まえると、数式の表す意味を読み取る（数式を言葉に翻訳できる）能力はとても大切ではないかと思います。

本書ではそこに焦点を当てており、とても興味深い書籍です。本書を読めば、これまでとは違う景色が見えるかもしれません。

意味がわかれば数学の風景が見えてくる改訂合本

created by Rinker

オススメその４

『生き抜くための高校数学高校数学の全範囲の基礎が完璧にわかる本』は、高校数学の総復習に使える読み物です。ベストセラーの「新体系・高校数学の教科書」シリーズ著者の最高傑作と名高い一冊です。

高校数学１，２，３，Ａ，Ｂ，Ｃというアラカルト方式でもなく、計算問題、公式・定理といったテーマ別でもなく、「全範囲」の基礎がたった１冊で完璧にわかる！

語りかけ口調の文章だから、授業を受けているような感覚で、自然と数学に親しめる

生きた題材や役立つ雑談、ビジュアル要素がもりだくさんだから、数学を身近に感じられ、理解が深まる

中学数学からつまずいてしまった高校生や受験生にも、数学を学び直したい大学生や社会人にも最適!

数学を学ぶことを通じて、論理的に考える力や、客観的に説明する力、試行錯誤する力が身につく

「この本ならば、最後までやり抜くことができる。数学に苦手意識を持つ大人にも子どもにも使える好著。」と佐藤優氏（作家・元外務省主任分析官）が大絶賛したのが本書。

目安としては、数学３まで学んでいれば「新体系シリーズ」、中学から高校までの数学をほとんど理解していなければ「生き抜くためのシリーズ」が向いているでしょう。