確率|独立な試行の確率について

今回は独立な試行の確率について学習しましょう。
一般に「独立試行」と言われ、問題でもよく扱われるテーマです。演習をたくさんこなして得点源にしたいところです。
よく「排反」と「独立」の2つの言葉を区別せずに使っている人がいますが、定義が異なるので文言通り覚え、演習をこなすことで違いを理解することが大切です。
記事の画像が見辛いときはクリックすると拡大できます。
独立な試行とその確率
「独立」という用語の説明の前に、「排反」についてもう一度確認しておきます。
「排反」は2つの事象の関係を表す用語で、2つの事象が同時に起こらない関係を表します。記憶が確かでない人は、中途半端なまま進むのではなく、もう一度しっかり確認しておきましょう。
このような「排反」に対して、「独立」という用語は試行に対して用いられます。対象にしているものが異なるので、しっかりと使い分けることが大切です。
独立な試行
「独立」は事象ではなく、試行どうしの関係を表す用語です。
一般に、2つの試行T1,T2があって、この2つの試行が互いに他方の結果に影響を及ぼさないとき、「2つの試行T1,T2は独立である」と言います。
1個のサイコロを2回投げる試行を考えてみましょう。このとき、2回の試行は互いに他方の結果に影響を及ぼしません。1回目の試行が、2回目の試行の結果に影響を与えないことは明らかです。
また、2つの試行T1,T2が互いに独立であるとき、試行T1の事象Aと試行T2の事象Bがともに起こる確率は、以下のように表されます。
互いに独立な試行T1,T2の事象A,Bがともに起こる確率
試行 $T_{\scriptsize{1}}$ の事象 $A$ が起こる確率を $P(A)$、試行 $T_{\scriptsize{2}}$ の事象 $B$ が起こる確率を $P(B)$ とする。
$2$ つの試行 $T_{\scriptsize{1}} \ , \ T_{\scriptsize{2}}$ が互いに独立であるとき、$2$ つの事象 $A \ , \ B$ がともに起こる確率は
\begin{align*} \quad P(A) \times P(B) \end{align*}事象なら排反かどうか、試行なら独立かどうか。誤用しないように気を付けよう。
独立な試行の確率を求めてみよう
独立な試行の確率を具体例で考えてみましょう。
独立な試行の例
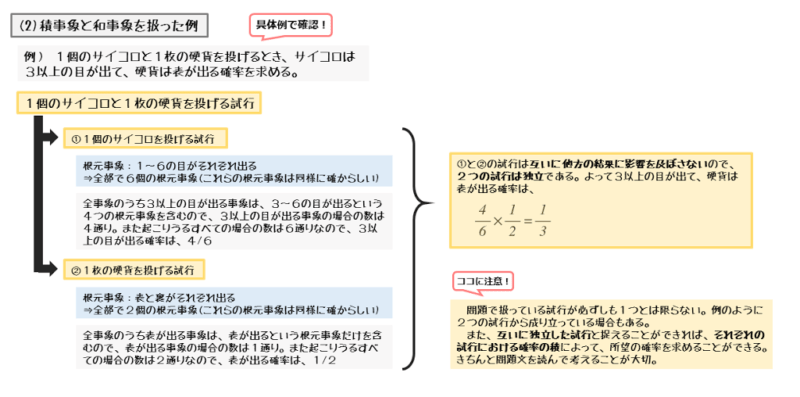
1個のサイコロと1枚の硬貨を投げるとき、サイコロは3以上の目が出て、硬貨は表が出る確率
互いに独立な試行を見つける
1個のサイコロと1枚の硬貨を投げるという試行は、細かく見ると、1個のサイコロを投げる試行と1枚の硬貨を投げる試行の2つの試行からなると捉えることができます。
1個のサイコロと1枚の硬貨を投げる試行
- 1個のサイコロを投げる試行
- 1枚の硬貨を投げる試行
この2つの試行について、サイコロの出目の結果と硬貨の表裏の結果とは互いに影響を及ぼしません。ですから、2つの試行は互いに独立な試行です。
互いに独立な試行では、互いの結果に影響を及ぼさないので、試行ごとに確率を考えることができます。
試行ごとに事象が起こる確率を求める
1個のサイコロを投げる試行について考えます。この試行で同様に確からしい根元事象は6個あります。
1個のサイコロを投げる試行での根元事象
- 1の目が出る事象
- 2の目が出る事象
- 3の目が出る事象
- 4の目が出る事象
- 5の目が出る事象
- 6の目が出る事象
これより、全事象の要素は6個になり、起こりうるすべての場合の数は6通りです。
このような根元事象をもとに3以上の目が出る事象を考えると、3~6の目が出る根元事象を要素にもつことが分かります。
以上のことから、1個のサイコロを投げる試行において、3以上の目が出る事象が起こる確率を求めます。
3以上の目が出る確率
$1$ 個のサイコロを振ったとき、$1 \ , \ 2 \ , \ \cdots \ , \ 6$ の目が出る。
これらは同様に確からしいので、起こりうるすべての場合の数は $6$ 通り。
そのうち、$3$ 以上の目が出る場合の数は $4$ 通りなので、$3$ 以上の目が出る確率は
\begin{align*} \quad \frac{4}{6}=\frac{2}{3} \end{align*}また、1枚の硬貨を投げる試行において、同様に確からしい根元事象は2個あります。
1枚の硬貨を投げる試行での根元事象
- 表が出る事象
- 裏が出る事象
これより、全事象の要素は2個になり、起こりうるすべての場合の数は2通りです。
このような根元事象をもとに表が出る事象を考えると、表が出る根元事象を要素にもつことが分かります。
以上のことから、1枚の硬貨を投げる試行において、表が出る事象が起こる確率を求めます。
表が出る確率
$1$ 枚の硬貨を投げたとき、表または裏が出る。
これらは同様に確からしいので、起こりうるすべての場合の数は $2$ 通り。
そのうち、表が出る場合の数は $1$ 通りなので、表が出る確率は
\begin{align*} \quad \frac{1}{2} \end{align*}互いに独立な試行がともに起こる確率を求める
1個のサイコロを投げる試行と1枚の硬貨を投げる試行とは互いに独立であることから、サイコロの目が3以上で、硬貨の表が出る確率は、3以上の目が出る事象が起こる確率と表が出る事象が起こる確率との積で求めることができます。
3以上の目が出て、表が出る確率
$1$ 個のサイコロを振ったとき、$1 \ , \ 2 \ , \ \cdots \ , \ 6$ の目が出る。
これらは同様に確からしいので、起こりうるすべての場合の数は $6$ 通り。
そのうち、$3$ 以上の目が出る場合の数は $4$ 通りなので、$3$ 以上の目が出る確率は
\begin{align*} \quad \frac{4}{6}=\frac{2}{3} \end{align*}$1$ 枚の硬貨を投げたとき、表または裏が出る。
これらは同様に確からしいので、起こりうるすべての場合の数は $2$ 通り。
そのうち、表が出る場合の数は $1$ 通りなので、表が出る確率は
\begin{align*} \quad \frac{1}{2} \end{align*}$1$ 個のサイコロを振る試行と $1$ 枚の硬貨を振る試行とは互いに独立なので、$3$ 以上の目が出て、硬貨の表が出る確率は
\begin{align*} \quad \frac{4}{6} \times \frac{1}{2} = \frac{1}{3} \end{align*}このように、ある試行がいくつかの独立な試行からなる場合、事象が起こる確率を試行ごとに考えることができます。これまでをまとめると以下のようになります。
独立な関係にある試行が複数あることを見抜ければ、所望の確率を求めることは難しくありません。演習をこなして、どんな場合が独立な試行なのかを把握しましょう。
独立な試行が見抜けなくても確率を求めることはできる
もちろん、起こりうるすべての場合の数や、3以上の目かつ表である事象が起こる場合の数から、所望の確率を求めることができます。こちらは基本的な確率の求め方です。
この場合、1個のサイコロと1枚の硬貨を投げる試行全体を1つの試行として扱っています。ですから、試行は1つだけで、独立かどうかを考える必要はありません。
サイコロの出目と硬貨の表裏の組合せの総数は、出目6通りのそれぞれについて、表裏2通りずつあります。
サイコロと硬貨の組合せの総数
$1$ 個のサイコロを振ったとき、目の出方は $1 \ , \ 2 \ , \ \cdots \ , \ 6$ の $6$ 通り。
この出目のそれぞれについて、$1$ 枚の硬貨の出方は表と裏の $2$ 通りずつある。
よって、$1$ 個のサイコロと $1$ 枚の硬貨を振ったときの出方の組合せの総数は
\begin{align*} \quad 6 \times 2 \ \text{(通り)} \end{align*}これが起こりうるすべての場合の数になります。
また、3以上の目かつ表である組合せの総数は、サイコロの出目4通りのそれぞれについて、硬貨の表1通りずつあります。
3以上の目かつ表である組合せの総数
$1$ 個のサイコロを振ったとき、$3$ 以上の目の出方は $4$ 通り。
この出目のそれぞれについて、表の出方は $1$ 通りずつある。
よって、$3$ 以上の目かつ表である組合せの総数は
\begin{align*} \quad 4 \times 1 \ \text{(通り)} \end{align*}これが3以上の目かつ表である事象が起こる場合の数になります。これより、求める確率は以下のようになります。
サイコロは3以上の目が出て、硬貨は表が出る確率
$1$ 個のサイコロを振ったとき、目の出方は $1 \ , \ 2 \ , \ \cdots \ , \ 6$ の $6$ 通り。
この出目のそれぞれについて、$1$ 枚の硬貨の出方は表と裏の $2$ 通りずつある。
よって、$1$ 個のサイコロと $1$ 枚の硬貨を振ったときの出方の組合せの総数は
\begin{align*} \quad 6 \times 2 \ \text{(通り)} \end{align*}$1$ 個のサイコロを振ったとき、$3$ 以上の目の出方は $4$ 通り。
この出目のそれぞれについて、表の出方は $1$ 通りずつある。
よって、$3$ 以上の目かつ表である組合せの総数は
\begin{align*} \quad 4 \times 1 \ \text{(通り)} \end{align*}したがって、サイコロは $3$ 以上の目が出て、硬貨は表が出る確率は
\begin{align*} \quad \frac{4 \times 1}{6 \times 2}=\frac{1}{3} \end{align*}これを計算すると、先ほどと同じ値を得ることができます。
ところで、この式を少し変形してみると、面白いことが分かります。
サイコロは3以上の目が出て、硬貨は表が出る確率
\begin{align*} \quad \frac{4 \times 1}{6 \times 2} = \underline{\frac{4}{6} \times \frac{1}{2}} \end{align*} \begin{align*} &\frac{4}{6} \cdots \text{サイコロを $1$ 回振って $3$ 以上の目が出る確率} \\[ 10pt ] &\frac{1}{2} \cdots \text{硬貨を $1$ 回振って表が出る確率} \end{align*}右辺(下線部分)は、独立な試行であることを利用したときの式です。独立な試行を利用する場合、全体の試行をいくつかの試行に小分けしたことが分かります。
全体の試行をいくつかの試行に小分けするメリットは、サイコロの出目と硬貨の表裏との組合せを考える必要がなくなることです。サイコロの出目や硬貨の表裏を単体で考えるのであれば、場合の数を数え間違えることはほとんどないはずです。
次は、実際に独立な試行を扱った問題を解いてみましょう。