図形と方程式|直線の方程式について

今回は、直線の方程式について学習しましょう。直線の方程式については中学ですでに学習しているので、比較的取り組みやすい単元かもしれません。
中学での学習内容をベースにしてさらに詳しく学習していきます。これまでの内容を意識しながら学習しましょう。
直線の方程式(傾き・切片)
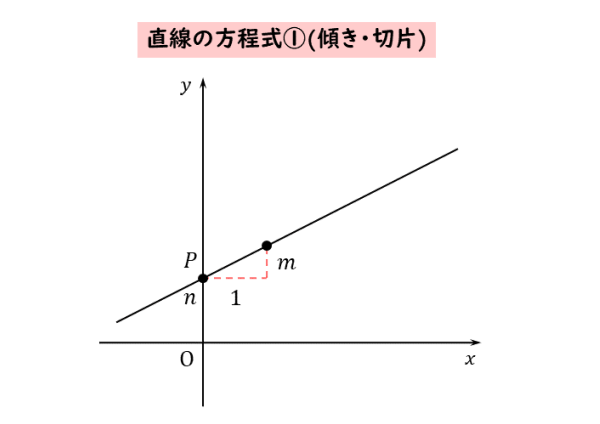
中学で学習した直線の方程式は、傾きと切片を用いて表された式です。グラフは以下の通りです。
比例の関係を表すグラフは原点を通る直線となります。それをy軸方向へ切片のぶんだけ平行移動したものが、直線の方程式が表すグラフです。
傾きは、xの増加量に対するyの増加量です。ですから、傾きのことを変化の割合と言うことがあります。
また、切片は、グラフとy軸との交点のy座標です。
直線の方程式を、傾きと切片を用いて表すと以下のようになります。
直線の方程式①
[1] 傾きを $m$、切片を $n$ とする直線の方程式は
\begin{align*} \quad y=mx+n \end{align*}[2] 点 $(p \ , \ 0)$ を通り、$x$ 軸に垂直な直線の方程式は
\begin{align*} \quad x=p \end{align*}[1]の式は、y軸に垂直な直線(傾きが0のとき)を含みますが、x軸に垂直な直線を含みません。そのために[2]の式があります。この2つですべての直線の式を表します。
すべての直線を表すことが1つの式でできないのは面倒です。ですから、以下のような一般形と言われる式があります。
直線の方程式の一般形
直線の方程式の一般形は
\begin{align*} \quad ax+by+c=0 \end{align*}ただし、$a \ , \ b \ , \ c$ は定数で、$a \neq 0$ または $b \neq 0$
一般形は、x軸に垂直な直線(b=0のとき)も含む式です。
この一般形での注意点は、定数aが傾きではないことです。同じ文字を用いているので注意しましょう。
一般形の式の利点は、すべての直線を表すことができることです。便利な式ですが、直線の方程式を求める問題で用いられることが多いとは言えません。
と言うのも、一般形の式には3つの定数の値a,b,cがあるからです。
直線の方程式を決定するには、3つの定数a,b,cの値を求める必要があります。つまり、3つの方程式を導く必要があるということです。
直線の方程式を求めために一般形を用いるのは、3点の座標が与えられている場合です。3点の座標を用いれば、3つの方程式を導出することができるからです。
しかし、3点の座標が与えられていても、一般形を用いることなく求めることもできます。
2点の座標から傾きを求め、残りの1点で切片を求めれば良いのです。ですから、一般形を積極的に用いる機会はあまり多くないかもしれません。
ただ、直線の方程式を求める問題は色々あります。ですから、一般形を用いた方が簡単に解ける問題もあります。
ここでは、直線を一般形で表すことができるということが理解できれば良いでしょう。
直線の方程式という用語について
方程式とは、雑な言い方をすれば、文字を使った等式のことですが、もう少し丁寧な言い方をすれば、変数に特定の数値(解)を代入したときにだけ等式が成立する式のことです。
これを踏まえて直線を表す式で考えてみると、等式が成り立つのは、グラフ上の点の座標を代入したときだけです。グラフ上にない点の座標を代入しても、等式は成り立ちません。
直線を表す式に、グラフ上の点の座標を代入すると、このときだけ等式が成立します。ですから、グラフ上の点の座標は、直線を表す式を方程式と見立てれば、その方程式の解と捉えることができます。
このことから、直線を表す式のことを一般に直線の方程式と言います。そして、グラフ上の点の座標は、直線の方程式の解となります。
直線の方程式(傾き・1点の座標)
傾きと切片の情報がともに分かっている場合は意外と少ないです。切片が不明な場合もあります。そのような場合では、傾きと1点の座標が分かっています。
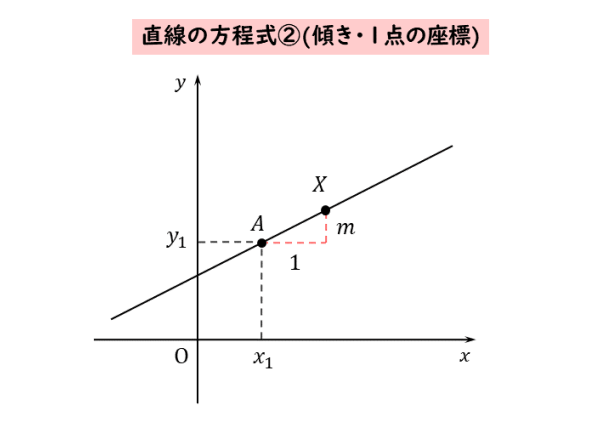
直線の方程式を、傾きと1点の座標を用いて表すと以下のようになります。
直線の方程式②
[1] 点 $(x_{1} \ , \ y_{1})$ を通り、傾きを $m$ とする直線の方程式は
\begin{align*} \quad y-y_{1}=m \left(x-x_{1} \right) \end{align*}[2] 点 $(x_{1} \ , \ y_{1})$ を通り、$x$ 軸に垂直な直線の方程式は
\begin{align*} \quad x=x_{1} \end{align*}先程と同じように、[1]の式ではx軸に垂直な直線を表せないので、[2]の式があります。
また、以下のようにして[1]の式を導出できます。
直線の方程式②の導出
直線の方程式を
\begin{align*} \quad y=mx+n \end{align*}とすると、点 $(x_{1} \ , \ y_{1})$ を通るので
\begin{align*} \quad y_{1}=m x_{1}+n \end{align*}$2$ つの等式を辺々引くと
\begin{align*} \quad y-y_{1}=mx-mx_{1} \end{align*}よって
\begin{align*} \quad y-y_{1}=m \left(x-x_{1} \right) \end{align*}これに点 $(x_{1} \ , \ y_{1})$ を代入すると等式を満たす。
等式の左辺どうし、右辺どうしをそれぞれ引くことを「辺々引く」と言います。辺々引くことで切片を消去しています。
ここで分かるのは、傾きとグラフ上の1点の座標とが分かれば、切片が不明でも直線の方程式を表すことができるということです。
傾きとグラフ上の1点の座標が分かれば、直線の方程式を表すことができる。
直線の方程式(2点の座標)
切片だけでなく、傾きの情報も不明である場合です。これからはこのような場合がほとんどです。この場合では、2点の座標が分かっています。
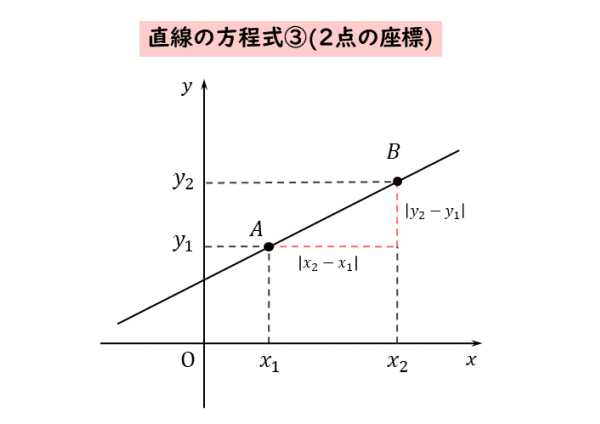
直線の方程式を、2点の座標を用いて表すと以下のようになります。
直線の方程式③
異なる $2$ 点 $(x_{1} \ , \ y_{1}) \ , \ (x_{2} \ , \ y_{2})$ を通る直線の方程式は
[1] $x_{1} \neq x_{2}$ のとき
\begin{align*} \quad y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \left(x-x_{1} \right) \end{align*}[2] $x_{1}=x_{2}$ のとき
\begin{align*} \quad x=x_{1} \end{align*}先程と同じように、[1]の式ではx軸に垂直な直線を表せないので、[2]の式があります。
また、以下のようにして[1]の式を導出できます。
直線の方程式③の導出
異なる $2$ 点 $(x_{1} \ , \ y_{1}) \ , \ (x_{2} \ , \ y_{2})$ を通るので、変化の割合は
\begin{align*} \quad \frac{y_{2}-y_{1}}{x_{2}-x_{1}} \quad \left(x_{1} \neq x_{2} \right) \end{align*}これは傾きに等しいので、これと点 $(x_{1} \ , \ y_{1})$ より
\begin{align*} \quad y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \left(x-x_{1} \right) \end{align*}導出するには、傾きが変化の割合に等しいことを利用します。
この性質は大切なのでしっかり覚えておきましょう。直線の方程式②の傾きmを変化の割合に置き換えただけです。
一般形のように、1つの式ですべての直線を表せた方が使い勝手が良いことは明らかです。ですから、以下のような式もあります。
直線の方程式③(応用)
\begin{align*} \quad y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \left(x-x_{1} \right) \end{align*}の両辺に $x_{2}-x_{1}$ を掛けると
\begin{align*} \quad \left(y_{2}-y_{1} \right) \left(x-x_{1} \right)-\left(x_{2}-x_{1} \right) \left(y-y_{1} \right)=0 \end{align*}これは $x_{2}=x_{1}$ のときも含む。
[1]の式の分母を両辺に掛けて整理しています。この式であれば、[2]の式も含むので、すべての直線を表すことができます。
分母を払っただけですが、効果は意外と侮れません。直線の方程式を機械的に求めることができるので、とても便利な方程式です。
軸に垂直な直線のことを意外と忘れがちなので、2点を通る直線の方程式を覚えるのであれば、分母を払った式の方が良いでしょう。
2点を通る直線の方程式
異なる $2$ 点 $(x_{1} \ , \ y_{1}) \ , \ (x_{2} \ , \ y_{2})$ を通る直線の方程式は
\begin{align*} \quad \left(y_{2}-y_{1} \right) \left(x-x_{1} \right)-\left(x_{2}-x_{1} \right) \left(y-y_{1} \right)=0 \end{align*}2点の座標が分かれば、応用しやすい直線の方程式を利用できるようにしておこう。
軸に垂直な直線の方程式
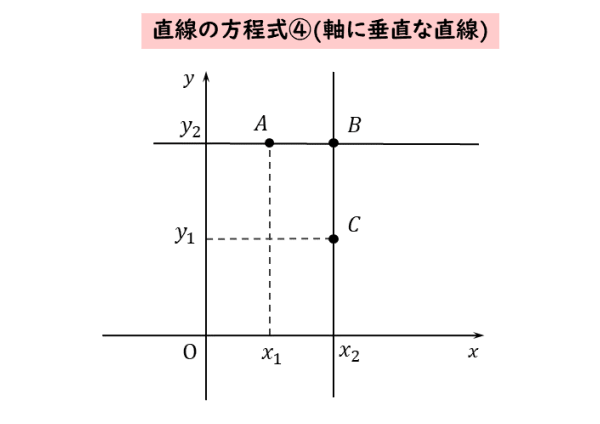
x軸やy軸に垂直な直線は、以下のようなグラフになります。
x軸に垂直な直線上にある点の座標は、x座標がつねに一定です。
同じように、y軸に垂直な直線上にある点の座標は、y座標がつねに一定です。
軸に垂直な直線の方程式
$3$ 点 $A \ , \ B \ , \ C$ の座標を
\begin{align*} &\quad A \ (x_{1} \ , \ y_{2} ) \\[ 7pt ] &\quad B \ (x_{2} \ , \ y_{2} ) \\[ 7pt ] &\quad C \ (x_{2} \ , \ y_{1} ) \end{align*}とする。このとき
直線 $AB$ の方程式は
\begin{align*} \quad y=y_{2} \end{align*}直線 $BC$ の方程式は
\begin{align*} \quad x=x_{2} \end{align*}x軸やy軸に垂直な直線では、傾きや切片を考える必要はありません。少し特殊なので注意しましょう。
直線の方程式を求めてみよう
直線の方程式の求め方は、与えられる情報に応じて異なります。問題で直線の方程式を求めるときには、どの情報が与えられているかを考えましょう。
例題
次の直線の方程式を求めよ。
$(1) \quad$ 点 $(-1 \ , \ 3)$ を通り、傾きが $4$ の直線
$(2) \quad$ $2$ 点 $(0 \ , \ 5) \ , \ (3 \ , \ 2)$ を通る直線
例題(1)の解答・解説
例題(1)
次の直線の方程式を求めよ。
$\quad$ 点 $(-1 \ , \ 3)$ を通り、傾きが $4$ の直線
傾きと1点の座標で表される直線の方程式に、与えられた傾きと座標を代入します。
例題(1)の解答例
点 $(-1 \ , \ 3)$ を通り、傾きが $4$ であるので
\begin{align*} \quad y-3=4 \left\{x-(-1) \right\} \end{align*}よって
\begin{align*} \quad y=4x+7 \end{align*}慣れてきたら、以下の式で覚えておくと良いでしょう。
直線の方程式(傾き・1点の座標)
点 $(x_{1} \ , \ y_{1})$ を通り、傾きを $m$ とする直線の方程式は
\begin{align*} \quad y-y_{1}=m \left(x-x_{1} \right) \end{align*}よって
\begin{align*} \quad y=m \left(x-x_{1} \right)+y_{1} \end{align*}初めから「y=」の形に代入するようにしておくと、符号ミスを減らせます。
例題(2)の解答・解説
例題(2)
次の直線の方程式を求めよ。
$\quad$ $2$ 点 $(0 \ , \ 5) \ , \ (3 \ , \ 2)$ を通る直線
2点の座標で表される直線の方程式に、与えられた座標を代入します。
例題(2)の解答例
$2$ 点 $(0 \ , \ 5) \ , \ (3 \ , \ 2)$ を通り、かつ $2$ 点の $x$ 座標が異なるので
\begin{align*} &\quad y-5=\frac{2-5}{3-0} \left(x-0 \right) \\[ 7pt ] &\quad y-5=-1 \cdot x \end{align*}よって
\begin{align*} \quad y=-x+5 \end{align*}公式を利用するにあたって、2点のx座標が異なることを断っておきましょう。
2点の座標を用いた公式を利用するとき、慣れないうちは代入ミスが多いです。公式を余白に書いたり、座標の上や下に対応する文字を書いたりすると代入ミスを減らせます。
次は、直線の方程式を扱った問題を実際に解いてみましょう。