図形と方程式|2直線の平行条件や垂直条件について

今回は、2直線の平行条件や垂直条件について学習しましょう。複数の直線を扱うことは頻繁にあり、それらの関係を考える問題もよく出題されます。
ここでは、平行や垂直という特徴的な関係が成り立つ条件について学習します。頻出の単元なので、演習をこなしておきましょう。
2直線の平行条件や垂直条件
2直線の平行条件
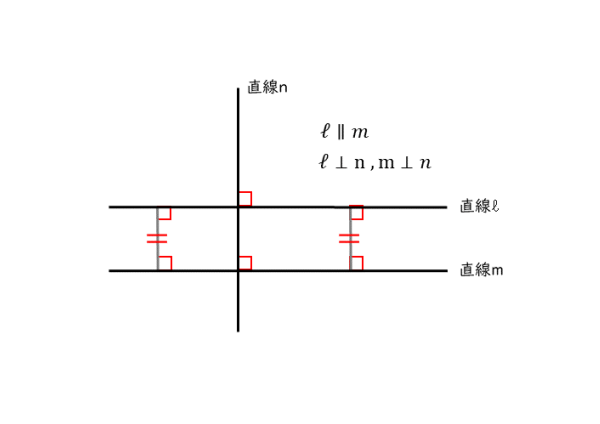
2直線が平行となるのは、2直線の間の距離がつねに一定であるときです。
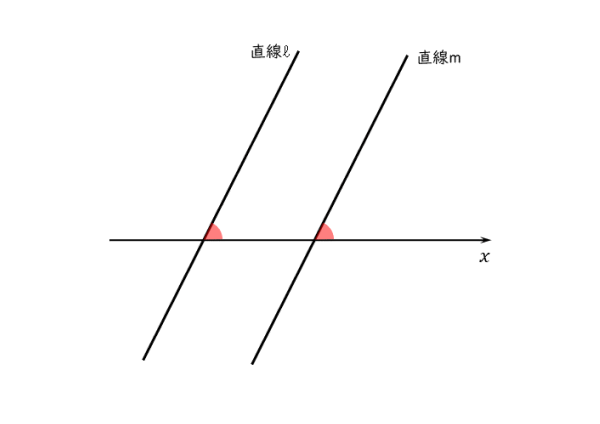
少し異なる視点で見ると、座標平面上における2直線が平行となるのは、直線とx軸とのなす角がともに等しくなるときです。
直線とx軸とのなす角とは、直線の傾きのことです。ですから、2直線が平行となるのは、直線の方程式で言えば、傾きの値がともに等しくなるときであると言えます。
2直線の平行条件①
$2$ 直線の方程式を
\begin{align*} &\quad y=m_{1}x+n_{1} \\[ 7pt ] &\quad y=m_{2}x+n_{2} \end{align*}とするとき、$2$ 直線が平行であれば
\begin{align*} \quad m_{1}=m_{2} \end{align*}が成り立つ。
ある直線に平行な直線の傾きを知りたいだけならば、この条件で足ります。
しかし、問題によっては、直線の方程式において、特定の項の係数を求める問題も出題されます。そういうわけで、一般形から導かれる平行条件も知っておく必要があります。
2直線の平行条件②
$2$ 直線の方程式を
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}とするとき、$2$ 直線が平行であれば
\begin{align*} \quad a_{1} b_{2}-a_{2} b_{1}=0 \end{align*}が成り立つ。
平行条件②の式は、2直線の方程式の係数が満たす関係式で、平行条件①の式を利用して得られます。導出してみましょう。
2直線の平行条件②の導出
$2$ 直線の方程式を
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \quad \cdots \text{①} \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \quad \cdots \text{②} \end{align*}とする。
[1] $\quad b_{1} \neq 0 \ , \ b_{2} \neq 0$ のとき
①より
\begin{align*} \quad y=-\frac{a_{1}}{b_{1}} x-\frac{c_{1}}{b_{1}} \end{align*}②より
\begin{align*} \quad y=-\frac{a_{2}}{b_{2}} x-\frac{c_{2}}{b_{2}} \end{align*}$2$ 直線が平行であるための条件は
\begin{align*} \quad -\frac{a_{1}}{b_{1}}=-\frac{a_{2}}{b_{2}} \end{align*}よって
\begin{align*} \quad a_{1} b_{2}-a_{2} b_{1}=0 \end{align*}[2] $\quad b_{1}=0$ のとき
①より
\begin{align*} \quad a_{1}x+c_{1}=0 \quad \cdots \text{③} \end{align*}③は $x$ 軸に垂直な直線となるので、③と②が平行であるためには
\begin{align*} \quad b_{2}=0 \end{align*}よって
\begin{align*} \quad b_{1}=b_{2}=0 \end{align*}したがって
\begin{align*} \quad a_{1} b_{2}-a_{2} b_{1}=0 \end{align*}が成り立つ。また、この逆も成り立つ。
[3] $\quad b_{2}=0$ のとき
[2]と同様にして成り立つ。
[1],[2],[3]より、$2$ 直線①,②が平行であるとき
\begin{align*} \quad a_{1} b_{2}-a_{2} b_{1}=0 \end{align*}このように2直線の平行条件は、傾きで考えた場合と、方程式の係数で考えた場合の2通りの表し方があります。
傾きを求めたいのか、それとも方程式の係数を求めたいのかに応じて使い分けましょう。
2直線の平行条件①+②
$2$ 直線
\begin{align*} &\quad y=m_{1}x+n_{1} \\[ 7pt ] &\quad y=m_{2}x+n_{2} \end{align*}が平行であるとき、平行条件は
\begin{align*} \quad m_{1}=m_{2} \end{align*}また、$2$ 直線
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}が平行であるとき、平行条件は
\begin{align*} \quad a_{1} b_{2}-a_{2} b_{1}=0 \end{align*}一般形の係数を用いた平行条件②の覚え方にはコツがあります。
2直線の方程式を上下に並べておき、「たすき掛けに係数を掛けてから引く」と簡単に覚えられます。垂直条件と併せて覚えると良いでしょう。
2直線の平行条件は、方程式を上下に並べて、たすき掛けに係数を掛けてから引く
2直線の垂直条件
2直線が垂直となるのは、2直線のなす角が90°になるときです。
このように2直線が垂直となるときの条件は、以下のようになります。
2直線の垂直条件①
$2$ 直線の方程式を
\begin{align*} &\quad y=m_{1}x+n_{1} \\[ 7pt ] &\quad y=m_{2}x+n_{2} \end{align*}とするとき、$2$ 直線が垂直であれば
\begin{align*} \quad m_{1} m_{2} =-1 \end{align*}が成り立つ。
垂直条件を導出するにあたって少し工夫しておきます。
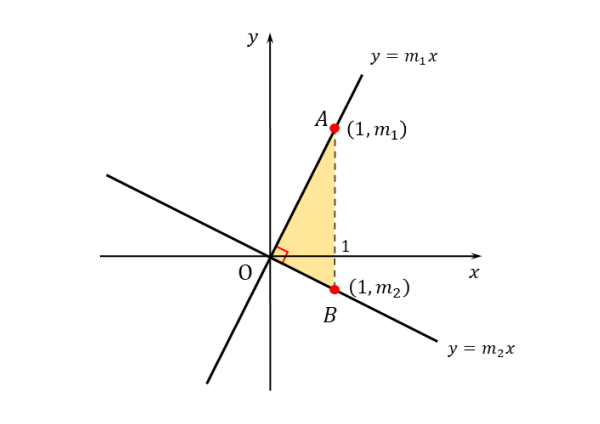
2直線が垂直であるとき、2直線を平行移動しても垂直であることは変わりません。直線の方程式を簡単にするために、原点を通るように平行移動します。
さらに、図のような直角三角形を考えます。x座標が1である2点A,Bもつくっておきます。
準備が整ったので、2直線の垂直条件を導出してみましょう。
2直線の垂直条件①の導出
$2$ 直線の方程式を
\begin{align*} &\quad y=m_{1}x+n_{1} \quad \cdots \text{①} \\[ 7pt ] &\quad y=m_{2}x+n_{2} \quad \cdots \text{②} \end{align*}とする。これらを原点を通るように平行移動すると
\begin{align*} &\quad y=m_{1}x \\[ 7pt ] &\quad y=m_{2}x \end{align*}また
\begin{align*} \quad A(1 \ , \ m_{1}) \ , \ B(1 \ , \ m_{2}) \end{align*}とすると、$\triangle OAB$ は $\angle A =90^{\circ}$ の直角三角形となる。
よって、三平方の定理より
\begin{align*} \quad AB^{2}=OA^{2}+OB^{2} \quad \cdots \text{③} \end{align*}ここで
\begin{align*} &\quad AB=m_{1}-m_{2} \\[ 7pt ] &\quad OA^{2}={m_{1}}^{2}+1 \\[ 7pt ] &\quad OB^{2}={m_{2}}^{2}+1 \end{align*}であるので、これらを③に代入して
\begin{align*} \quad \left( m_{1}-m_{2} \right)^{2}=\left( {m_{1}}^{2}+1 \right)+\left( {m_{2}}^{2}+1 \right) \end{align*}整理すると
\begin{align*} \quad m_{1} m_{2}=-1 \end{align*}この垂直条件は、垂直な2直線であれば必ず成り立ちます。
また、平行条件のときと同じように、一般形から導かれる垂直条件も知っておく必要があります。
2直線の垂直条件②
$2$ 直線の方程式を
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}とするとき、$2$ 直線が垂直であれば
\begin{align*} \quad a_{1} a_{2}+b_{1} b_{2}=0 \end{align*}が成り立つ。
垂直条件②の式は、2直線の方程式の係数が満たす関係式で、垂直条件①の式を利用して得られます。導出してみましょう。
2直線の垂直条件②の導出
$2$ 直線の方程式を
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \quad \cdots \text{①} \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \quad \cdots \text{②} \end{align*}とする。
[1] $\quad b_{1} \neq 0 \ , \ b_{2} \neq 0$ のとき
①より
\begin{align*} \quad y=-\frac{ a_{1} }{ b_{1} } x-\frac{ c_{1} }{ b_{1} } \end{align*}②より
\begin{align*} \quad y=-\frac{ a_{2} }{ b_{2} } x-\frac{ c_{2} }{ b_{2} } \end{align*}$2$ 直線が垂直であるための条件は
\begin{align*} \quad \left(-\frac{ a_{1} }{ b_{1} } \right) \left(-\frac{ a_{2} }{ b_{2} } \right)=-1 \end{align*}よって
\begin{align*} \quad a_{1} a_{2}+b_{1} b_{2}=0 \end{align*}[2] $\quad b_{1}=0$ のとき
①より
\begin{align*} \quad a_{1}x+c_{1}=0 \quad \cdots \text{③} \end{align*}③は $x$ 軸に垂直な直線となるので、③と②が垂直であるためには
\begin{align*} \quad a_{2}=0 \end{align*}よって
\begin{align*} \quad a_{2}=b_{1}=0 \end{align*}したがって
\begin{align*} \quad a_{1} a_{2}+b_{1} b_{2}=0 \end{align*}が成り立つ。また、この逆も成り立つ。
[3] $\quad b_{2}=0$ のとき
[2]と同様にして成り立つ。
[1],[2],[3]より、$2$ 直線①,②が垂直であるとき
\begin{align*} \quad a_{1} a_{2}+b_{1} b_{2}=0 \end{align*}2直線の垂直条件も平行条件と同じように、傾きで考えた場合と、方程式の係数で考えた場合の2通りの表し方があります。
求めるものが直線の傾きなのか、それとも方程式の係数なのかに応じて使い分けましょう。
2直線の垂直条件①+②
$2$ 直線
\begin{align*} &\quad y=m_{1}x+n_{1} \\[ 7pt ] &\quad y=m_{2}x+n_{2} \end{align*}が垂直であるとき、垂直条件は
\begin{align*} \quad m_{1} m_{2}=-1 \end{align*}また、$2$ 直線
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}が垂直であるとき、垂直条件は
\begin{align*} \quad a_{1} a_{2}+ b_{1} b_{2}=0 \end{align*}平行条件②と同様に、一般形の係数を用いた垂直条件②の覚え方にはコツがあります。
一般形の係数から導く垂直条件は、2直線の方程式を上下に並べておき、「上下に並んだ係数を掛けてから足す」と導出できます。
2直線の垂直条件は、方程式を上下に並べて、上下に並んだ係数を掛けてから足す
次は、2直線の平行条件や垂直条件を利用して、2直線が平行か垂直かを調べてみましょう。
2直線が平行か垂直かを調べてみよう
平行条件や垂直条件を利用して、2直線の関係を調べてみましょう。
例題
次の $2$ 直線は、平行であるか。また、垂直であるか。
\begin{align*} &(1) \quad y=-3x+1 \ , \ y=-3x-2 \\[ 7pt ] &(2) \quad y=2x+4 \ , \ y=-\frac{1}{2}x+3 \end{align*}例題(1)の解答・解説
例題(1)
次の $2$ 直線は、平行であるか。また、垂直であるか。
\begin{align*} \quad y=-3x+1 \ , \ y=-3x-2 \end{align*}2直線の傾きを調べます。一般形ではないので、すぐに分かります。
例題(1)の解答例
$2$ 直線
\begin{align*} &\quad y=-3x+1 \\[ 7pt ] &\quad y=-3x-2 \end{align*}の傾きはともに $-3$ で一致する。
よって、$2$ 直線は平行である。
2直線の傾きが一致すれば、2直線は平行です。
2直線の平行条件:2直線の傾きが一致する
2直線の平行条件
$2$ 直線
\begin{align*} &\quad y=m_{1}x+n_{1} \\[ 7pt ] &\quad y=m_{2}x+n_{2} \end{align*}が平行であるとき、平行条件は
\begin{align*} \quad m_{1}=m_{2} \end{align*}また、$2$ 直線
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}が平行であるとき、平行条件は
\begin{align*} \quad a_{1} b_{2}-a_{2} b_{1}=0 \end{align*}例題(2)の解答・解説
例題(2)
次の $2$ 直線は、平行であるか。また、垂直であるか。
\begin{align*} \quad y=2x+4 \ , \ y=-\frac{1}{2}x+3 \end{align*}例題(1)と同じ要領で解きます。
例題(2)の解答例
$2$ 直線
\begin{align*} &\quad y=2x+4 \\[ 7pt ] &\quad y=-\frac{1}{2}x+3 \end{align*}の傾きの積を調べると
\begin{align*} \quad 2 \times \left(-\frac{1}{2} \right)=-1 \end{align*}よって、$2$ 直線は垂直である。
2直線の垂直条件:2直線の傾きの積=-1
2直線の傾きが一致しなければ、垂直条件を満たすか調べましょう。
2直線の垂直条件
$2$ 直線
\begin{align*} &\quad y=m_{1}x+n_{1} \\[ 7pt ] &\quad y=m_{2}x+n_{2} \end{align*}が垂直であるとき、垂直条件は
\begin{align*} \quad m_{1} m_{2}=-1 \end{align*}また、$2$ 直線
\begin{align*} &\quad a_{1}x+b_{1}y+c_{1}=0 \\[ 7pt ] &\quad a_{2}x+b_{2}y+c_{2}=0 \end{align*}が垂直であるとき、垂直条件は
\begin{align*} \quad a_{1} a_{2}+ b_{1} b_{2}=0 \end{align*}次は、2直線の平行条件や垂直条件を扱った問題を実際に解いてみましょう。