数学１,数学Ａ
今さら、センター試験の過去問を解いても意味がないと思うかもしれません。もちろん、共通テストになったためにセンター試験とは形式の変わる部分が出てきますが、問題のレベルに大きな差があるとは考えられません。
形式に慣れることは難しいかもしれません。しかし、センター試験の過去問から、自分の学力レベルを把握することができるでしょう。入試レベルへの到達度を知ることは、とても大切なことです。
今回は、2017年1月14・15日に実施された、センター試験の数学１・Ａの第１問についてです。
第１問は「数と式」や「２次関数」からの出題ですが、難易度は去年並みの評価のようです。過去問に類似した問題が出題されたので、充分な対策ができていればより易しく感じたかもしれません。
やはり過去問を解いておくことは大切です。
１，２年生の中には、この時季から本格的に受験対策を始める人もいます。受験に成功する人に共通するのは、準備に取り掛かるのが早いことです。
また、受験に成功する人は、日常的に受験に直結する学習をしています。その場しのぎではなく、３カ月後、半年後、１年後の自分の学力を意識しながら学習するのが大切ではないかと思います。
大学進学の意思があれば、実際の入試問題を解き、自分の現在の学力を客観的に把握しましょう。解けないことが問題ではなく、自分の足りない部分を知らないことが問題です。
要求される学力と自分の学力とのギャップを埋めるのが受験対策です。
模範解答とは言えませんが、解き方や考え方の参考になれば幸いです。あくまでも一例なので鵜呑みにせず、自分なりに解答例を考えてみると良いでしょう。質の高い学習になります。
記事の画像が見辛いときはクリックすると拡大できます。
数学１・Ａの第１問について
第１問は、数１の「数と式」と「２次関数」の単元からの出題でした。各単元の出題内容をまとめると以下のようになります。
第１問の出題内容
第１問〔１〕，〔２〕…「数と式」からの出題
〔１〕「式の値」に関する問題
〔２〕「集合と命題」に関する問題
第１問〔３〕…「２次関数」からの出題
式変形や最小値に関する問題
どちらの単元も教科書例題レベルなので、ぜひ完答したい問題です。
「数と式」の計算では、このレベルの数式を余裕で扱えないと、完全に準備不足です。「２次関数」の式変形でも、数学２・Ｂのことを考えると、煩雑ではありますが、それほど難しい変形ではないでしょう。
数学の効果的な対策としては、例題を反復し、確実にかつ速やかに解けるレベルに仕上げることが遠回りのようで実は近道。例題は初歩的な定石で、これらを組み合わせて問題が作られる。
６０分間（共通テストでは７０分）で解かなければならないので、「確実に」だけでは足りません。「確実に」解けるようになったら、次は「速やかに」解けるようにしましょう。
短時間で処理できる計算力を問われている。準備では計算のスピードも意識しよう。
第１問〔１〕について
第１問〔１〕は「数や式」を扱った問題です。
設問を読みながら、与えられた条件や押さえておきたい事柄が目立つようにしましょう。線引きしたり、囲んだりすると見落としがありません。
設問全体を俯瞰してみると、「さらに」や「また」という言葉があるので、３部構成であることが分かります。
第１問〔１〕は小問３つから構成されています。
第１問〔１〕
解くことに集中しているとどうしても視野が狭くなる。ヒントになる条件は解くときに必ず利用するので、見落とさない工夫をしよう。
解答欄アイ
小問を通してすべて「式の値」に関する問題です。
解答欄アイについて、情報を整理すると以下のようになります。
解答欄アイ
条件
\begin{align*}
&\quad x \ \text{は正の実数} \\[ 5pt ]
&\quad x^{\scriptsize{2}}+ \frac{4}{x^{\scriptsize{2}}} = 9 \ \text{を満たす}
\end{align*}
求めるもの
\begin{equation*}
\quad \left( x + \frac{2}{x} \right)^{\scriptsize{2}} \ \text{の値}
\end{equation*}
第１問〔１〕
条件式を利用するために、与式を乗法公式で展開します。分数を扱いますが、慌てず丁寧に展開しましょう。
解答欄アイの解答例 1⃣
\begin{align*}
&\left(x+\frac{2}{x} \right)^{\scriptsize{2}} \\[ 7pt ]
= \ &x^{\scriptsize{2}} + 2 \cdot x \cdot \frac{2}{x} + \left( \frac{2}{x} \right)^{\scriptsize{2}} \\[ 7pt ]
= \ &\underline{ x^{\scriptsize{2}} + \frac{4}{x^{\scriptsize{2}}} } + 4
\end{align*}
ここでは、与式を展開しましたが、条件式を平方完成して与式を導くこともできます。ただ、分数を扱うので、展開の方が解きやすいでしょう。
展開して整理すると、条件式に対応する箇所（下線部分）ができます。条件式を代入して計算すると、解を得ることができます。
解答欄アイの解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&= \underline{ x^{\scriptsize{2}} + \frac{4}{x^{\scriptsize{2}}} } + 4 \\[ 7pt ]
&\text{ここで} \\[ 5pt ]
&\quad x^{\scriptsize{2}}+ \frac{4}{x^{\scriptsize{2}}} = 9 \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad x^{\scriptsize{2}} + \frac{4}{x^{\scriptsize{2}}} +4=9+4=13 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad \left(x+\frac{2}{x} \right)^{\scriptsize{2}}=13 \quad \cdots \text{アイ}
\end{align*}
解答欄アイは次の行にも出てきます。すでに解答は分かっていますが、求めておきます。
求めるもの
\begin{equation*}
x + \frac{2}{x} \ \text{の値}
\end{equation*}
ｘ＋２/ｘの値を求めるには、両辺の平方根をとります。
このときに注意したいのは、等式を満たす平方根には、正の平方根と負の平方根があることです。
第１問〔１〕
条件によれば、ｘは正の実数であるので、２/ｘも正の実数です。これを考慮して解きます。
解答欄アイの解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad \left(x+\frac{2}{x} \right)^{\scriptsize{2}}=13 \quad \cdots \text{アイ} \\[ 7pt ]
&\text{$x$ は正の実数であるので} \\[ 5pt ]
&\quad x+\frac{2}{x} \gt 0 \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad x+\frac{2}{x}= \sqrt{13}
\end{align*}
平方根には正の平方根と負の平方根の２つがある。条件に注意しよう。
解答欄アイの解答例をまとめると以下のようになります。
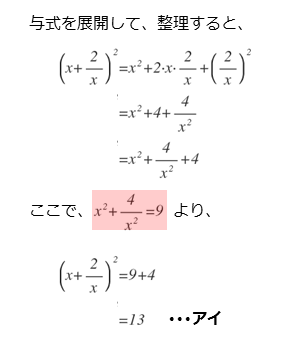解答欄アイの解答例①
解答欄アイの解答例②
解答欄ウ・エオカ
次の小問は、３乗公式を扱った問題です。
現在の教科書では、３乗公式は発展問題扱いになっているようですが、教科書で扱っているのでしっかりマスターしておきましょう。
発展の内容でも、数学２・Ｂや数学３のことを考えてマスターしておこう。
解答欄アイを含めて、既知の情報を確認しておきます。また、求めるもの（解答欄ウ・エオカ）も確認します。
解答欄ウ・エオカ
既知のもの
\begin{align*}
&\quad x \ \text{は正の実数} \\[ 5pt ]
&\quad x^{\scriptsize{2}}+ \frac{4}{x^{\scriptsize{2}}} = 9 \\[ 7pt ]
&\quad \left(x+ \frac{2}{x} \right)^{\scriptsize{2}} = 13 \\[ 7pt ]
&\quad x+ \frac{2}{x} = \sqrt{13}
\end{align*}
求めるもの
\begin{equation*}
\quad x^{\scriptsize{3}} + \frac{8}{x^{\scriptsize{3}}} \ \text{の変形とその値}
\end{equation*}
第１問〔１〕
解答欄から、次の３乗公式を利用できそうです。
３乗公式
\begin{equation*}
a^{\scriptsize{3}}+b^{\scriptsize{3}} = \left(a+b \right) \left(a^{\scriptsize{2}}-ab+b^{\scriptsize{2}} \right)
\end{equation*}
この３乗公式に当てはめて整理します。
解答欄ウの解答例
\begin{align*}
&a=x \ , \ b=\frac{2}{x} \ \text{より} \\[ 5pt ]
&x^{\scriptsize{3}} + \frac{8}{x^{\scriptsize{3}}} \\[ 7pt ]
= \ &\left(x+\frac{2}{x} \right) \left(x^{\scriptsize{2}}-x \cdot \frac{2}{x} +\frac{4}{x^{\scriptsize{2}}} \right) \\[ 7pt ]
= \ &\left(x+\frac{2}{x} \right) \left(x^{\scriptsize{2}}+\frac{4}{x^{\scriptsize{2}}}-2 \right) \quad \cdots \text{ウ}
\end{align*}
解答例アイと同様に、対応する等式を利用して式の値を求めます。
解答欄エオカの解答例
\begin{align*}
&\quad \vdots \\[ 7pt ]
&= \ \left(x+\frac{2}{x} \right) \left(x^{\scriptsize{2}}+\frac{4}{x^{\scriptsize{2}}}-2 \right) \quad \cdots \text{ウ} \\[ 7pt ]
&\text{ここで} \\[ 5pt ]
&\quad x^{\scriptsize{2}}+ \frac{4}{x^{\scriptsize{2}}} = 9 \\[ 7pt ]
&\quad x+ \frac{2}{x} = \sqrt{13} \\[ 7pt ]
&\text{より}
\end{align*}
\begin{align*}
\quad \left(x+\frac{2}{x} \right) \left(x^{\scriptsize{2}}+\frac{4}{x^{\scriptsize{2}}}-2 \right) &= \sqrt{13} \cdot \left(9-2 \right) \\[ 7pt ]
&= 7\sqrt{13}
\end{align*}
\begin{align*}
&\text{したがって} \\[ 5pt ]
&\quad x^{\scriptsize{3}} + \frac{8}{x^{\scriptsize{3}}} = 7\sqrt{13} \quad \cdots \text{エオカ}
\end{align*}
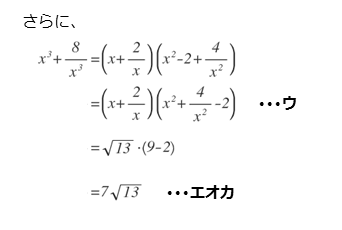解答欄ウ・エオカの解答例
先に求めた値も利用するので、計算ミスで全滅しないように。答案の書き方にも気を付けよう。
解答欄キク
次の小問は、４次の項が出てきます。４乗公式は習っていないので、これまでの情報で解決できないかを考えます。
解答欄キク
既知のもの
\begin{align*}
&\quad x \ \text{は正の実数} \\[ 5pt ]
&\quad x^{\scriptsize{2}}+ \frac{4}{x^{\scriptsize{2}}} = 9 \\[ 7pt ]
&\quad \left(x+ \frac{2}{x} \right)^{\scriptsize{2}} = 13 \\[ 7pt ]
&\quad x+ \frac{2}{x} = \sqrt{13} \\[ 7pt ]
&\quad x^{\scriptsize{3}}+ \frac{8}{x^{\scriptsize{3}}} = 7\sqrt{13}
\end{align*}
求めるもの
\begin{equation*}
\quad x^{\scriptsize{4}} + \frac{16}{x^{\scriptsize{4}}} \ \text{の値}
\end{equation*}
第１問〔１〕
与えられた２次式の両辺を２乗すると、４次の項が出てきます。このことに気付けば、注意するのは計算ミスだけです。
条件式である２次式の両辺を２乗して、等式を整理します。
解答欄キクの解答例
\begin{align*}
&\quad x^{\scriptsize{2}}+\frac{4}{x^{\scriptsize{2}}}=9 \\[ 7pt ]
&\text{の両辺を $2$ 乗すると}
\end{align*}
\begin{align*}
\quad \left(x^{\scriptsize{2}}+\frac{4}{x^{\scriptsize{2}}} \right)^{\scriptsize{2}} &= 9^{\scriptsize{2}} \\[ 7pt ]
x^{\scriptsize{4}} +2 \cdot x^{\scriptsize{2}} \cdot \frac{4}{x^{\scriptsize{2}}} + \left( \frac{4}{x^{\scriptsize{2}}} \right)^{\scriptsize{2}} &= 81 \\[ 7pt ]
x^{\scriptsize{4}} +8 + \frac{16}{x^{\scriptsize{4}}} &= 81 \\[ 7pt ]
x^{\scriptsize{4}} + \frac{16}{x^{\scriptsize{4}}} &= 73 \quad \cdots \text{キク}
\end{align*}
展開の工夫と言っても良いですが、一度は見かけたことのある問題なので、難易度はそれほど高くありません。
また、乗法公式を変形した式を利用しても良いでしょう。
乗法公式を変形して利用する
\begin{align*}
&\quad \left(a+b \right)^{\scriptsize{2}}=a^{\scriptsize{2}}+2ab+b^{\scriptsize{2}} \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad a^{\scriptsize{2}}+b^{\scriptsize{2}}=\left(a+b \right)^{\scriptsize{2}}-2ab
\end{align*}
乗法公式を利用した解答例は以下のようになります。
解答欄キクの別解例全体的にすぐに方針の立つ計算問題なので、ミスなく速やかに解きたい問題です。早い人だと５分も掛からないでしょう。
第１問〔１〕のポイントと解答例をまとめると以下のようになります。 ポイントだけなく、注意点もまとめてあります。ノートにまとめるときの参考になれば幸いです。
第１問〔１〕のポイントと解答例 次は、第１問〔２〕を解いてみましょう。
