数学1・A|2017センター試験・第3問を解いてみよう

今さら、センター試験の過去問を解いても意味がないと思うかもしれません。もちろん、共通テストになったためにセンター試験とは形式の変わる部分が出てきますが、問題のレベルに大きな差があるとは考えられません。
形式に慣れることは難しいかもしれません。しかし、センター試験の過去問から、自分の学力レベルを把握することができるでしょう。入試レベルへの到達度を知ることは、とても大切なことです。
今回は、2017年センター試験数学1・Aの第3問についてです。
例年と比べると、出題の形式や内容が履修内容の理解度を問われるものだったように感じます。ですから、暗記で終わっている人には難しく感じたのではないかと思われます。
「本質を理解する」という意味では、良問ではないかと思います。このようなレベルの問題を日頃からこなせるようになりたいものです。
記事の画像が見辛いときはクリックすると拡大できます。
数学I・Aの第3問について
第3問は、数A「場合の数と確率」の単元からの出題でした。出題の題材や内容をまとめると以下のようになります。
出題内容(題材:3人が順番に引くくじ引き)
- 少なくとも1人が当たりくじを引く問題
- 事象を排反な3つの事象に分割して考える問題
- 3種類の条件付き確率の大小関係に関する問題
頻出の余事象を扱った確率や条件付き確率をはじめ、「排反」の言葉の意味を理解しているかなどの問題が出題されました。
これまでの出題内容や形式とは若干趣が異なったので、特に「排反」に関する問題では面食らった人が多かったかもしれません。ただ何となく確率を求めていた人には完答するのが難しかったと思われます。
「本質の理解」の大切さを改めて感じさせる問題。このような良問を日頃から数多く解いておきたい。
第3問の全体像を掴もう
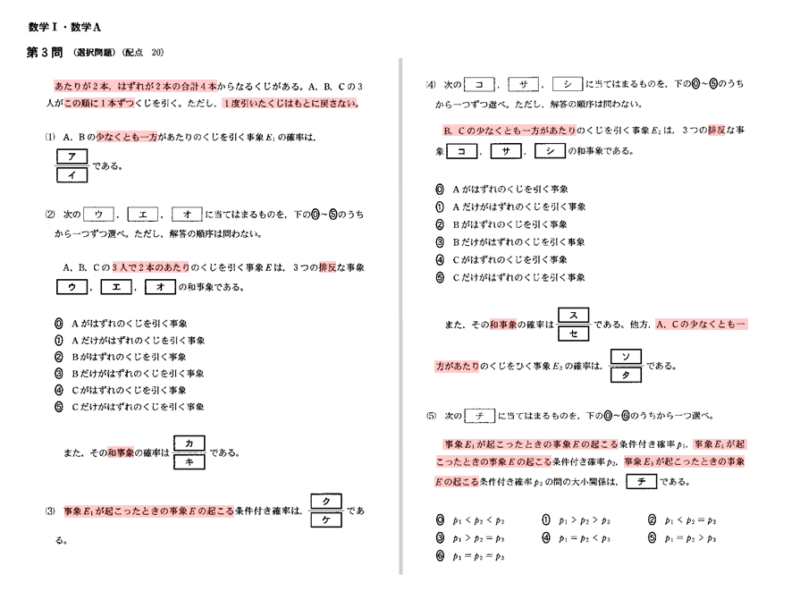
第3問は以下のような問題でした。
全体を俯瞰してみると、(1)~(5)の小問形式になっています。特に最後の問題は、それまでが解けていないと正しい選択肢を選ぶことができない問題です。
問題を解くのに共通していたのは、与えられた条件を満たす場合をすべて書き出せたかどうかだと思います。
日頃から事象を書き出す習慣の有無が、得点に大きく影響したのではないかと思います。手を動かしてイメージを膨らませる習慣はどの科目でも有効なので、ぜひとも習慣にしておきましょう。
第3問で扱われている題材とそのルール
以下の条件で色々な確率を求める。
- 当たり2本、はずれ2本の合計4本のくじを、A,B,Cの順番に1本ずつ引く。ただし、引いたくじは戻さない。
- 引いたくじは戻さないので、反復試行ではない。
第3問(1)
解答欄アイ
小問(1)は解答欄アイに関する問題です。
解答欄アイ
$A \ , \ B$ の少なくとも一方があたりのくじを引く事象 $E_{1}$ の確率

「少なくとも」という文言があるので、余事象を利用して求めます。
「少なくとも」という文言を見たら、余事象を使ってみよう。
事象E1の余事象は「A,Bがともにはずれのくじを引く事象」です。この余事象の確率は、「Aがはずれを引く確率」×「Bがはずれを引く確率」×「Cがあたりを引く確率」で求めることができます。
「Aがはずれを引く確率」は、4本のくじのうちはずれの2本のどちらかを引けば良いので、2/4=1/2です。
次に「Bがはずれを引く確率」は、Aが引いて3本になった状態から残ったはずれの1本を引けば良いので、1/3です。
最後に「Cがあたりを引く確率」は、当たりだけしか残っておらず何を引いても問題ないので、2/2=1です。これらの積を取れば、余事象が起こる確率です。
余事象の確率を求めた後は「1-(余事象の確率)」を計算すれば事象E1の確率を得ることができます。
解答欄アイの解答例をまとめると以下のようになります。
解答例の解き方は実は条件付き確率を利用した解き方
複数の試行を行っていても反復試行でない場合、次の試行の結果は前の試行の結果に影響を受けます(独立ではないから)。
このような場合、前の試行の結果が起こったことを前提に次の試行の結果を考えているので、条件付き確率を考えていることになります。
この考え方で解かない場合、3人がくじを引いた結果(場合の数)を数えあげて確率を求めることになります。
3人がくじを引いた結果から確率を求める
3人のくじの引き方は全部で
\begin{align*} \quad 4 \times 3 \times 2=24 \ \text{(通り)} \end{align*}また、$A \ , \ B$ がともにはずれを引き、$C$ があたりを引く引き方(余事象)は全部で
\begin{align*} \quad 2 \times 1 \times 2=4 \ \text{(通り)} \end{align*}よって、余事象の確率は
\begin{align*} \quad \frac{4}{24}=\frac{1}{6} \end{align*}余事象を利用しないで求める場合
もちろん、余事象を利用せず、直接的に事象E1の確率を求めることもできます。
「A,Bの少なくとも一方があたりのくじを引く」事象をすべて書き出します。
「A,Bの少なくとも一方があたりのくじを引く」事象
$A \ , \ B$ の少なくとも一方があたりのくじを引く事象を書き出すと
($A \ , \ B \ , \ C$)=(当,当,は),(当,は,当),(当,は,は),(は,当,当),(は,当,は)
の $5$ 通りある。
全部で5通り考えらます。あたりのくじは2本しかないので、3人ともあたりを引くことはないことに注意しましょう。
それぞれの事象の確率を求めると、すべて1/6になります。ここで、各事象は互いに排反であることを考慮すると、求める確率は和で求めて5/6になります。
今回は後の問題のことを考えると、こちらの方が良かったかもしれません。
第3問(2)
解答欄ウエオ,カキ
小問(2)は解答欄ウエオ,カキに関する問題です。
解答欄ウエオ,カキ
$A \ , \ B \ , \ C$ の $3$ 人で $2$ 本のあたりのくじを引く事象 $E$ に関する問題

「3人で2本のあたりのくじを引く」と言っても、あたりのくじを引くのがAとBの場合やAとCの場合など合があります。
この場合の事象Eは、いくつかの事象を含むことが分かります。また、各事象は問題文にもある通り、3つあり、かつ互いに排反です。
「3人で2本のあたりのくじを引く」ときの結果を書き出してみます。
「3人で2本のあたりのくじを引く」事象
$3$ 人で $2$ 本のあたりのくじを引く事象を書き出すと
($A \ , \ B \ , \ C$)=(当,当,は),(当,は,当),(は,当,当)
の $3$ 通りある。
全部で3通りあることが分かります。3つの事象は同時に起こらないので、互いに排反であると言えます。
互いに排反な3つの事象
- (当,当,は):Cだけがはずれを引く事象
- (当,は,当):Bだけがはずれを引く事象
- (は,当,当):Aだけがはずれを引く事象
このように事象Eは互いに排反な3つの事象からなるので、3つの事象の和事象で求められます。
3つの排反な事象が起こる確率はともに1/6です。これらの確率の和から、事象Eの確率が1/2であることが分かります。
次の問題を意識しながら解こう
小問(1)だけを考えれば、余事象を利用して解くことは悪くありません。ただ、小問(2)のことを考えると方針とは言えないかもしれません。
もし、小問(1)で余事象を利用せずに解いていれば、小問(2)では計算なしで解くことができたかもしれません。
解答欄ウエオ,カキの解答例をまとめると以下のようになります。
第3問(3)
解答欄クケ
小問(3)は解答欄クケに関する問題です。
解答欄クケ
事象 $E_{1}$ が起こるときの事象 $E$ の起こる条件付き確率 $P_{E_{1}}(E)$

条件付き確率の公式を上手に利用したいところです。
条件付き確率の公式
事象 $A$ が起こったときの事象 $B$ が起こる条件付き確率 $P_{A}(B)$ は
\begin{align*} \quad P_{A}(B) &= \frac{n \left(A \cap B \right)}{n \left( A \right)} \\[ 7pt ] &= \frac{P \left(A \cap B \right)}{P \left( A \right)} \end{align*}条件付き確率 $P_{A}(B)$ は、事象 $A$ が全事象になり、その事象 $A$ の中で共通部分となる事象 $A \cap B$ が起こる確率を求めたもの。
小問(3)で公式を使うためには、文字の対応関係を把握しなければなりません。
小問(3)の条件付き確率
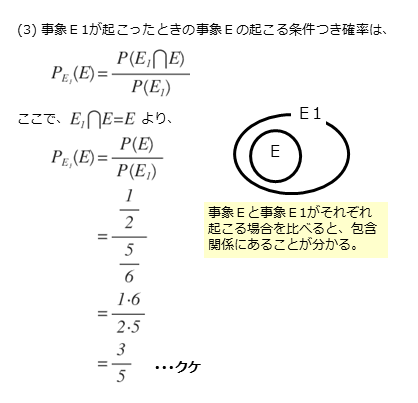
事象 $E_{1}$ が起こるときの事象 $E$ の起こる条件付き確率 $P_{E_{1}}(E)$ は
\begin{align*} \quad P_{E_{1}}(E) &= \frac{n \left(E_{1} \cap E \right)}{n \left( E_{1} \right)} \\[ 7pt ] &= \frac{P \left(E_{1} \cap E \right)}{P \left( E_{1} \right)} \end{align*}小問(3)で条件付き確率を求めるには、2つの事象E1,Eの共通部分E1⋂Eを求めなければなりません。
小問(1),(2)できちんと結果を書き残しておけば、簡単に共通部分E1⋂Eに関する場合の数や確率を求めることができるでしょう。
「A,Bの少なくとも一方があたりのくじを引く」ときの結果(事象E1)を書き出してみます。
「A,Bの少なくとも一方があたりのくじを引く」事象
$A \ , \ B$ の少なくとも一方があたりのくじを引く事象を書き出すと
($A \ , \ B \ , \ C$)=(当,当,は),(当,は,当),(当,は,は),(は,当,当),(は,当,は)
の $5$ 通りある。
全部で5通りあります。
また、「3人で2本のあたりのくじを引く」ときの結果(事象E)を書き出してみます。
「3人で2本のあたりのくじを引く」事象
$3$ 人で $2$ 本のあたりのくじを引く事象を書き出すと
($A \ , \ B \ , \ C$)=(当,当,は),(当,は,当),(は,当,当)
の $3$ 通りある。
これらは$A \ , \ B$ の少なくとも一方があたりのくじを引く事象にすべて含まれている。
全部で3通りあります。
これらの共通の結果を調べてみると、事象Eはすべて事象E1に含まれていることに気付きます。つまり、E1⋂E=Eとなります。
共通部分E1⋂Eの場合の数が得られたので、あとは公式から条件付き確率を求めます。
小問(3)の条件付き確率
事象 $E_{1}$ が起こるときの事象 $E$ の起こる条件付き確率 $P_{E_{1}}(E)$ は
\begin{align*} \quad P_{E_{1}}(E) = \frac{P \left(E_{1} \cap E \right)}{P \left( E_{1} \right)} \end{align*}ここで、事象 $E_{1}$ が起こる場合の数は $5$ 通り、事象 $E$ が起こる場合の数は $3$ 通りある。
また
\begin{align*} \quad E_{1} \cap E = E \end{align*}であるので、求める条件付き確率は
\begin{align*} \quad P_{E_{1}}(E) &= \frac{n \left(E_{1} \cap E \right)}{n \left( E_{1} \right)} \\[ 7pt ] &= \frac{n \left(E \right)}{n \left( E_{1} \right)} \\[ 7pt ] &= \frac{3}{5} \end{align*}解答欄クケの解答例をまとめると以下のようになります。こちらでは場合の数ではなく、確率を用いています。
次は、第3問(4)を解いてみましょう。