数学1・A|2017センター試験・第4問を解いてみよう

今さら、センター試験の過去問を解いても意味がないと思うかもしれません。もちろん、共通テストになったためにセンター試験とは形式の変わる部分が出てきますが、問題のレベルに大きな差があるとは考えられません。
形式に慣れることは難しいかもしれません。しかし、センター試験の過去問から、自分の学力レベルを把握することができるでしょう。入試レベルへの到達度を知ることは、とても大切なことです。
今回は、2017年1月14・15日に実施された、センター試験の数学1・Aの第4問についてです。
センター試験(大学入学共通テストに改名)でも「整数」に関する問題が出題されるようになりましたが、意外と苦手意識をもつ人が多い印象があります。特に、難関大学の個別試験(2次試験)ではよく扱われます。
マーク形式とは言え、入試レベルなのでしっかりこなせるようにしておきたいものです。そのためにも、やはり過去問を解いておくことは大切です。
1,2年生の中には、この時季から本格的に受験対策を始める人もいます。受験に成功する人に共通するのは、準備に取り掛かるのが早いことです。
また、受験に成功する人は、日常的に受験に直結する学習をしています。その場しのぎではなく、3カ月後、半年後、1年後の自分の学力を意識しながら学習するのが大切ではないかと思います。
大学進学の意思があれば、実際の入試問題を解き、自分の現在の学力を客観的に把握しましょう。解けないことが問題ではなく、自分の足りない部分を知らないことが問題です。
要求される学力と自分の学力とのギャップを埋めるのが受験対策です。
模範解答とは言えませんが、解き方や考え方の参考になれば幸いです。あくまでも一例なので鵜呑みにせず、自分なりに解答例を考えてみると良いでしょう。質の高い学習になります。
記事の画像が見辛いときはクリックすると拡大できます。
数学1・Aの第4問について
数学1・Aの第4問は数A「整数の性質」からの出題でした。ベースになるのは小学校で学習した約数や倍数などです。
しかし、単に数値を求めるだけでなく、整数の性質を論理的に説明したり、理解したりする問題が比較的多いのが特徴だと思います。要するに証明問題がよく出題されるということです。
このことは特に数Aの単元全般に言えることだと思います。ですから、基本的な計算はもちろんですが、じっくりと思考することを意識して学習しておきましょう。
整数の「性質」を学ぶ単元なので、それを理解しているかを問われるのは当たり前。計算できるのはもちろんだが、論理的な思考力が身に付くような学習を日頃から行いたい。
第4問の全体像を掴もう
第4問は以下のような問題でした。
全体を俯瞰してみると、(1)~(3)の小問形式になっています。特に、(1),(2)が連動していることに注意しましょう。
また、(3)では(1),(2)とは異なる数を扱っています。そういうわけで、第4問は、(1),(2)の前半部分と、(3)の後半部分の2部構成になっていると考えられます。
条件を満たす数をきちんと書き出し、それらを吟味すれば完答を狙えたでしょう。
第4問(1)
解答欄アイ
(1)は解答欄アイに関する問題です。
解答欄アイ
百の位の数が $3$、十の位の数が $7$、一の位の数が $a$ である $3$ 桁の自然数を $37a$ と表記する。
$37a$ が $4$ で割り切れるときの $a$ の値
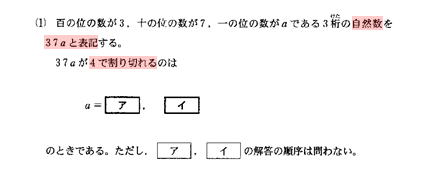
3桁の自然数を37aと表記することに注意しましょう。このまま用いると間違えてしまいます。
また、3桁の自然数は、4で割り切れるので4の倍数になります。整数の性質を知っているかどうかが問われています。
4の倍数は、下2桁の数が4の倍数である数。
3桁の自然数37aの下2桁は7aです。十の位の数が7と分かっているので、一の位の数だけを考えればよいことが分かります。
一の位の数には0,1,…,9の9つの候補があります。これらから1つずつ選んで作った2桁の数70,71,…,79の数を4で割っていき、割り切れる数を見つければ良いでしょう。
70,71,…,79のうち、4の倍数になるのは72,76の2つです。
解答欄アイの解答例をまとめると以下のようになります。
3桁の数を式で表す
3桁の数を式で表すことができます。これを利用して解く問題が出題されることもあります。
3桁の数を便宜上、abcと表記します。このとき、abcをそのまま計算で使うことはできません。あくまでも便宜上の表記だからです。
3桁の数abcを式で表すと以下のように表せます。
3桁の数 $abc$ を式で表す
\begin{align*} &100 \times a + 10 \times b + 1 \times c \\[ 7pt ] = \ &100a + 10b + c \end{align*}100をa個、10をb個、1をc個集めた数を3桁の数abcと考えるのがポイント。
第4問(2)
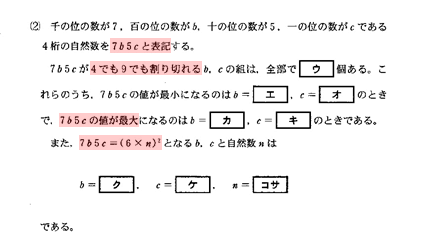
(1)では3桁の自然数でしたが、(2)では4桁の自然数になっています。条件も変わっているので注意しましょう。
解答欄ウ
(2)の解答欄ウに関する問題です。
解答欄ウ
千の位の数が $7$、百の位の数が $b$、十の位の数が $5$、一の位の数が $c$ である $4$ 桁の自然数を $7b5c$ と表記する。
$7b5c$ が $4$ でも $9$ でも割り切れる $b \ , \ c$ の組の個数

4でも9でも割り切れる自然数とは、4の倍数かつ9の倍数のことです。4桁の自然数7b5cは、4の倍数である条件に加えて、9の倍数である条件も満たす必要があります。
4の倍数は、下2桁の数が4の倍数である数。9の倍数は、各位の和が9の倍数である数。
4桁の自然数7b5cが4の倍数であるので、下2桁の数5cが4の倍数になります。50,51,…,59から4の倍数を探すと、52,56の2つです。これより、c=2,6です。
また、4桁の自然数7b5cが9の倍数であるので、各位の数の和を求めるとb+c+12です。これとc=2,6の結果を利用してbの値を求めます。
b,cの組を探す
$c=2$ のとき、各位の数の和は
\begin{align*} \quad b+c+12 &=b+2+12 \\[ 7pt ] &=b+14 \end{align*}これが $9$ の倍数になるのは $b=4$ のとき
また、$c=6$ のとき、各位の数の和は
\begin{align*} \quad b+c+12 &=b+6+12 \\[ 7pt ] &=b+18 \end{align*}これが $9$ の倍数になるのは $b=0 \ , \ 9$ のとき
したがって、$b \ , \ c$ の組は
\begin{align*} (b \ , \ c)=(4 \ , \ 2) \ , \ (0 \ , \ 6) \ , \ (9 \ , \ 6) \end{align*}の $3$ 個ある。
先にcの値を求めておいて、bについての条件式からbの値を求めています。その結果、b,cの組が3組あることが分かりました。b=0のときを忘れそうなので注意しましょう。
解答欄ウの解答例をまとめると以下のようになります。
解答例は個別試験(2次試験)で記述することを考えたときの一例です。マーク形式の試験では、上述したように、条件式に代入して探していく解き方で充分でしょう。
解答欄エオ,カキ
(2)の解答欄エオ,カキに関する問題です。
解答欄エオ,カキ
千の位の数が $7$、百の位の数が $b$、十の位の数が $5$、一の位の数が $c$ である $4$ 桁の自然数を $7b5c$ と表記する。
$4$ 桁の自然数 $7b5c$ が $4$ でも $9$ でも割り切れる $b \ , \ c$ の組のうち、$7b5c$ の値が最小または最大になる $b \ , \ c$ の値

解答欄ウで求めた3個のb,cの組から、4桁の自然数7b5cが最小または最大となるものを見つけます。
3個のb,cの組を実際に代入して調べます。
4桁の自然数7b5cの最大値と最小値
$3$ 個の $b \ , \ c$ の組は
\begin{align*} (b \ , \ c)=(4 \ , \ 2) \ , \ (0 \ , \ 6) \ , \ (9 \ , \ 6) \end{align*}であるので、$4$ 桁の自然数 $7b5c$ はそれぞれ
\begin{align*} \quad 7452 \ , \ 7056 \ , \ 7956 \end{align*}よって、$7b5c$ の値が最小になるのは
\begin{align*} \quad b=0 \ , \ c=6 \end{align*}のときで、$7b5c$ の値が最大になるのは
\begin{align*} \quad b=9 \ , \ c=6 \end{align*}のときである。
解答欄エオ,カキの解答例をまとめると以下のようになります。
解答欄ク,ケ,コサ
(2)の解答欄ク,ケ,コサに関する問題です。
解答欄ク,ケ,コサ
千の位の数が $7$、百の位の数が $b$、十の位の数が $5$、一の位の数が $c$ である $4$ 桁の自然数を $7b5c$ と表記する。
$7b5c={(6 \times n)}^{2}$ となる $b \ , \ c \ , \ n$ の値

4桁の自然数7b5cが積の形で表されているので、因数分解をしたときの話です。
4桁の自然数7b5cは7056,7452,7956と分かっているので、それぞれ変形して確かめます。その前に、(6×n)2=36×n2と変形しておきます。
ここで、どうして与式のようなものが出てきたのかを考えてみましょう。
4桁の自然数7b5cは4でも9でも割り切れる数でした。4でも9でも割り切れるということは、4の倍数かつ9の倍数、言い換えると36の倍数であるということです。
つまり、4桁の自然数7b5cは、36を因数にもつ数になります。このことから、与式が出てくるわけです。
4桁の自然数7b5cのイメージが湧いたところで、3つの数7056,7452,7956を36でそれぞれ割り算し、残りの数がn2の形になるか吟味します。
3つの数を因数分解する
$4$ 桁の自然数 $7452 \ , \ 7056 \ , \ 7956$ を $36$ でそれぞれ割り算すると
\begin{align*} &\quad 7056 \div 36 = 196 = {14}^{2} \\[ 7pt ] &\quad 7452 \div 36 = 207 = 9 \times 23 \\[ 7pt ] &\quad 7956 \div 36 = 221 \end{align*}よって
\begin{align*} \quad 7056 &= 36 \times 196 \\[ 7pt ] &= 6^{2} \times 14^{2} \\[ 7pt ] &= \left(6 \times 14 \right)^{2} \end{align*}したがって
\begin{align*} \quad b=0 \ , \ c=6 \ , \ n=14 \end{align*}3個のb,cの組のうち、b=0,c=6のときだけが与式を満たすことが分かります。
解答欄ク,ケ,コサの解答例をまとめると以下のようになります。
次は、第4問(3)を解いてみましょう。















