数学２
今回は、２重解をもつ条件について学習しましょう。扱う方程式は、２次方程式ではなく、３次方程式になります。
３次式を因数分解できなければならないので、不安な人は復習しながら進めていきましょう。
３次方程式の問題の取り組み方
３次方程式を扱った問題では、１次式と２次式の積に因数分解することが基本方針です。
３次式を因数分解するためには、因数となる１次式を見つけることが最優先です。因数となる１次式が見つかれば、組立除法を用いて割り算できます。割り算によって２次式の商が分りますが、この商が残りの因数となります。
３次方程式が２重解をもつ条件
３次方程式は最大で３つの実数解をもちます。この３つの解がすべて同じであれば、３重解と言います。また、３つのうち２つが同じであれば、２重解と言います。
２次方程式のときと異なり、３つの解がすべて同じときと、２つの解が同じときがあるので、３重解や２重解と区別できる言い方になっています。
このような３次方程式において、２重解をもつ条件を考えてみましょう。
３次方程式が１次式と２次式の積に因数分解できたとすると、すぐに思いつくのは、２次式から得られる２次方程式が重解をもつ場合です。
しかし、これだけではありません。２次方程式がもつ異なる２つの実数解のうち、１次式から得られる方程式の解と同じものがあるかもしれません。つまり、３次方程式が２重解をもつ可能性は２通りあるということです。
３次方程式が２重解をもつ条件
$3$ 次方程式が $1$ 次式 $x-\alpha$ と $2$ 次式 $g(x)$ の積に因数分解できるとき
\begin{equation*}
\quad \left( x-\alpha \right) \ g(x)=0
\end{equation*}
と表せる。
このとき、$3$ 次方程式が $2$ 重解をもつのは
[１] $2$ 次方程式 $g(x)=0$ が $x=\alpha$ でない重解をもつ。
[２] $2$ 次方程式 $g(x)=0$ の解の $1$ つが $x=\alpha$ で、他の解は $x=\alpha$ でない。
の $2$ 通りが考えられる。
３次方程式が２重解をもつ条件を考えるときは、場合分けして、それぞれの場合で解かなければなりません。重解は２次方程式でよく扱われるので、[１]の場合だけで安心しがちです。[２]の場合を見落とさないようにしましょう。
３次方程式が２重解をもつ条件を決定してみよう
３次方程式が２重解をもつ条件を決定してみましょう。
例題
$3$ 次方程式
\begin{equation*}
\quad x^{\scriptsize{3}}+(a-1)x^{\scriptsize{2}}+(4-a)x-4=0
\end{equation*}
が $2$ 重解をもつように、定数 $a$ の値を求めよ。
例題の解答・解説
３次方程式を扱った問題なので、まず因数分解することを考えましょう。剰余の定理と因数定理から、３次式の因数となる１次式を探します。
例題の解答例 1⃣
\begin{align*}
&\quad f(x)=x^{\scriptsize{3}}+\left(a-1 \right)x^{\scriptsize{2}}+\left(4-a \right)x-4 \\[ 7pt ]
&\text{とすると} \\[ 5pt ]
&\quad f(1)=1^{\scriptsize{3}}+\left(a-1 \right) \cdot 1^{\scriptsize{2}}+\left(4-a \right) \cdot 1-4=0 \\[ 7pt ]
&\text{より、$f(x)$ は $x-1$ を因数にもつ。}
\end{align*}
因数となる１次式が分かったら、組立除法で３次式を割り算します。組立除法の結果は以下の通りです。
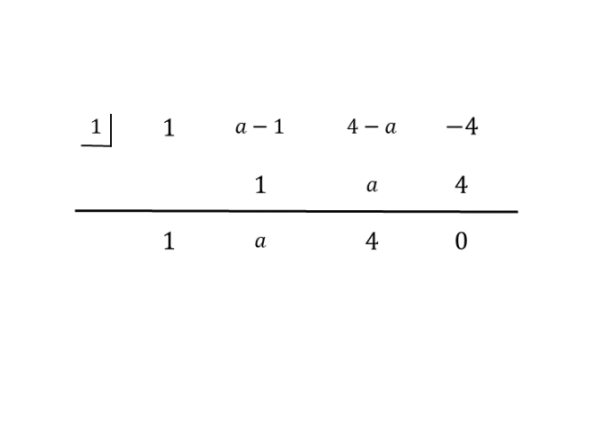例題の組立除法 ３次式を因数分解できたら、与えられた３次方程式を因数分解した形にします。この因数分解の結果から、解を求めるための方程式を新たに導きます。
例題の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\text{より、$f(x)$ は $x-1$ を因数にもつ。} \\[ 5pt ]
&\text{よって} \\[ 5pt ]
&\quad f(x)=\left( x-1 \right) \left( x^{\scriptsize{2}}+ax+4 \right) \\[ 7pt ]
&\text{より、方程式は} \\[ 5pt ]
&\quad \left( x-1 \right) \left( x^{\scriptsize{2}}+ax+4 \right)=0 \\[ 7pt ]
&\text{したがって} \\[ 5pt ]
&\quad x-1=0 \quad \text{または} \quad x^{\scriptsize{2}}+ax+4=0
\end{align*}
３次方程式の解の１つは、１次方程式からすぐに分かります。この解をもとに場合分けをして、２重解をもつときの条件、言い換えると定数ａの値を求めます。つまり、２重解をもつ条件は定数ａによって決まるということです。
まず、２次方程式が重解をもつときです。ただし、１次方程式の解とは異なることも忘れないようにしましょう。
例題の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad x-1=0 \quad \text{または} \quad x^{\scriptsize{2}}+ax+4=0 \\[ 7pt ]
&\text{[１] $x^{\scriptsize{2}}+ax+4=0$ が $1$ ではない重解をもつ} \\[ 5pt ]
&\text{判別式を $D$ とすると} \\[ 5pt ]
&\quad D=0 \quad \text{かつ} \quad 1^{\scriptsize{2}}+a \cdot 1+4 \neq 0 \\[ 7pt ]
&\text{を満たせばよい。ここで} \\[ 5pt ]
&\quad D=a^{\scriptsize{2}}-16=\left(a+4 \right) \left(a-4 \right) \\[ 7pt ]
&\text{より、$D=0$ とすると} \\[ 5pt ]
&\quad a=\pm 4 \\[ 7pt ]
&\text{これは $a+5 \neq 0$ を満たす。}
\end{align*}
３次方程式は最大で３つの解をもつので、誤って３重解にならないように気を付けましょう。判別式の条件だけでは、２次方程式が重解をもつことは言えても、ｘ＝１を解にもたないことは言えません。
それを踏まえて２次方程式がｘ＝１を解にもたないという条件を付けています。２次方程式に特定の解をもたせないために、その解を代入しても等式が成り立たない（≠を用います）とします。
２次方程式に解でない値を代入しても、等式は成り立たない。等式を成り立たせたくなければ、≠を使う。
次は、２次方程式の解の１つが１となる（１次方程式の解と同じになる）ときです。もちろん、２次方程式の残りの解は１になってはいけません。
例題の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\text{[２] $x^{\scriptsize{2}}+ax+4=0$ の解の $1$ つが $1$ で、他の解が $1$ ではない} \\[ 5pt ]
&\text{$x=1$ が解であるので} \\[ 5pt ]
&\quad 1^{\scriptsize{2}}+a \cdot 1+4= 0 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad a+5=0 \quad \text{すなわち} \quad a=-5 \\[ 7pt ]
&\text{このとき、$2$ 次方程式は} \\[ 5pt ]
&\quad x^{\scriptsize{2}}-5x+4=0 \\[ 7pt ]
&\text{となるので} \\[ 5pt ]
&\quad \left(x-1 \right) \left(x-4 \right)=0 \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad x=1 \ , \ 4 \\[ 7pt ]
&\text{これは、他の解が $1$ ではないので適する。} \\[ 5pt ]
&\text{[１]，[２]から、求める定数 $a$ の値は} \\[ 5pt ]
&\quad a=\pm 4 \ , \ -5
\end{align*}
定数ａの値が分かったら、２次方程式の解をきちんと確認しましょう。与えられた３次方程式が２重解をもつのは、定数ａの値によって３通りあることが分かります。
組立除法が上手くいかないとき
係数に文字が含まれると、筆算はもちろんですが、組立除法でも難しく感じるかもしれません。そんなときは、最低次数の文字（ここでは定数ａ）について整理すると、３次式を因数分解できます。
最低次数の文字に注目して因数分解する
\begin{align*}
&\quad x^{\scriptsize{3}}+(a-1)x^{\scriptsize{2}}+(4-a)x-4=0 \\[ 7pt ]
&\text{方程式の左辺を $a$ について整理すると} \\[ 5pt ]
&\quad x^{\scriptsize{3}}-x^{\scriptsize{2}}+4x-4+a \left(x^{\scriptsize{2}}-x \right)=0 \\[ 7pt ]
&\text{さらに変形すると} \\[ 5pt ]
&\quad x^{\scriptsize{2}} \left(x-1 \right)+4 \left(x-1 \right)+ax \left(x-1 \right)=0 \\[ 7pt ]
&\text{共通因数 $x-1$ でくくると} \\[ 5pt ]
&\quad \left(x-1 \right) \left(x^{\scriptsize{2}}+ax+4 \right)=0
\end{align*}
２次方程式の因数分解でも扱った解法です。複数の文字がある場合、最低次数の文字に注目して変形します。この解法では、因数となる１次式が分かっていなくても因数分解できるところが利点です。
次は、３次方程式が２重解をもつ条件を扱った問題を実際に解いてみましょう。
