集合と論理|必要条件と十分条件、同値について

今回は「必要条件や十分条件、同値」について学習しましょう。
特に必要・十分条件を扱った問題は、センター試験(大学入学共通テスト)でも毎年出題されるほど頻出です。それにも関わらず、意外と苦手にしている人が多いのも事実です。
この単元を得点源にできるとだいぶ有利になるので、しっかりマスターしておきましょう。
記事の画像が見辛いときはクリックすると拡大できます。
必要条件・十分条件
すでに学習済みですが、命題のうちxやaなどの変数を含む文や式のことを特に「条件」と言います。
そして、このような条件を2つ用いて1つの命題にしたものが、命題「p⇒q」です。命題「p⇒q」において、条件pを仮定、条件qを結論と言います。
必要条件や十分条件は、命題「p⇒q」における条件p,qの関係を表す用語です。
十分条件
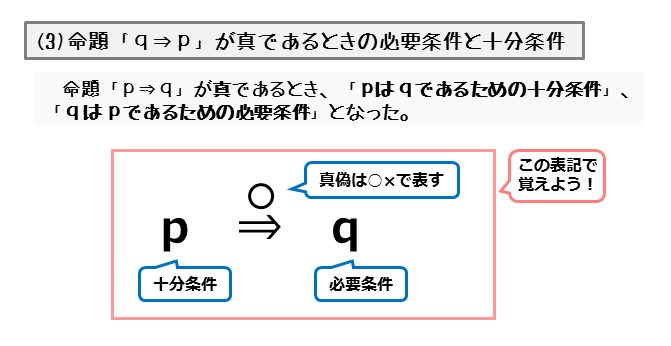
命題「p⇒q」が真であるとします。このとき、仮定である条件pは、結論である条件qが成り立つには十分な仮定になります。
このとき、結論qに対する仮定pのことを「十分条件」と言います。一般に、命題「p⇒q」が真であるとき、「pはqであるための十分条件である」と言います。
条件q(結論)が成り立つために、条件pが絶対に必要かと言うと、そうでもありません。他にも結論を成り立たせる条件があるからです。条件qが成り立つには、必ずしも必要ではありませんが、十分な条件です。
このことは、集合P,Qの包含関係をイメージすると理解しやすいでしょう。
「命題「p⇒q」が真であるとき、pはqであるための十分条件」とは、仮定pは結論qから見れば、仮定として十分な条件という意味です。
仮定は、結論にとって十分であっても必要ではない。
2つの条件の関係から、一方が十分条件になる例を挙げます。
条件が十分条件になる例
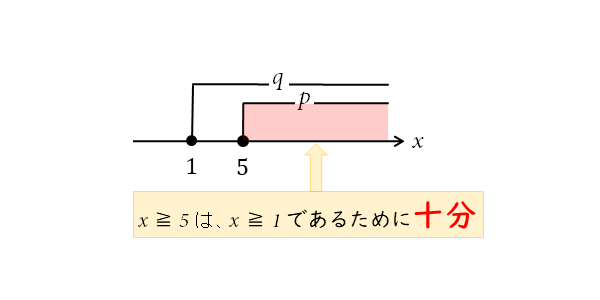
条件 $p \ , \ q$ について
\begin{align*} &\quad p \ : \ x \geqq 5 \\[ 7pt ] &\quad q \ : \ x \geqq 1 \end{align*}であるとする。
数直線を見ると、x≧5であるために、x≧1であることは条件として十分ではあります。
しかし、それが必要かと言われればそうとは言い切れません。
このことから、「x≧5はx≧1であるための十分条件ではあるが、必要条件ではない」となります。
必要条件
命題「p⇒q」が真であるとします。このとき、結論である条件qは、仮定である条件pから必然的に導かれる結論になります。
このとき、仮定pに対する結論qのことを「必要条件」と言います。一般に、命題「p⇒q」が真であるとき、「qはpであるための必要条件である」と言います。
「命題「p⇒q」が真であるとき、qはpであるための十分条件」とは、結論qは仮定pから見れば、結論として必要な条件という意味です。
結論は仮定の行きつく先なので、仮定にとって必要な条件。
2つの条件の関係から、一方が必要条件になる例を挙げます。
必要条件になる例
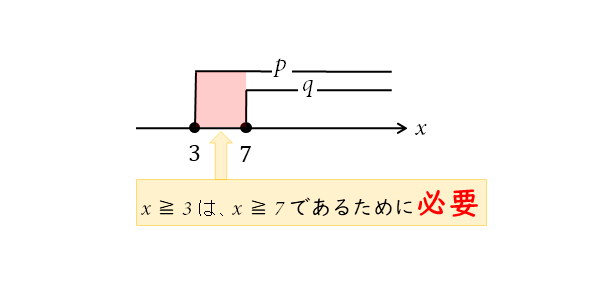
条件 $p \ , \ q$ について
\begin{align*} &\quad p \ : \ x \geqq 3 \\[ 7pt ] &\quad q \ : \ x \geqq 7 \end{align*}であるとする。
数直線を見ると、x≧7であるために、x≧3であることは条件として必要です。
しかし、それで十分かと言われればそうとは言い切れません。
このことから、「x≧3はx≧7であるための必要条件ではあるが、十分条件ではない」と言えます。
具定例として少し分かりにくいかもしれません。この例では、命題「p(x≧3)⇒q(x≧7)」が偽で、命題「q(x≧7)⇒p(x≧3)」が真です。ですから、結論になるのは条件p(x≧3)の方です。
結論p(x≧3)は、仮定q(x≧7)から見れば、十分ではないが必要な条件になります。
図解して必要条件と十分条件を考えよう
この単元で頭を悩ませるのは、2つの条件p,qが必要条件と十分条件のどちらになるかということです。苦手意識のある人も多いかもしれません。
しかし、集合や要素に置き換え、さらにベン図を使えば、その悩みは解決します。
条件pが真となる変数の値を要素とする集まりを集合P、条件qが真となる変数の値を要素とする集まりを集合Qとします。
命題「p⇒q」が真であるとき、2つの集合P,Qの関係を考えてみましょう。
すでに学習済みですが、集合Pは集合Qの部分集合になります。ですから、2つの集合にはP⊂Qという包含関係があります。
命題の真偽と集合の包含関係
命題「 $p \Rightarrow q$ 」が真である
⇔ $P \ , \ Q$ には $P \subset Q$ という包含関係がある
P⊂Qであるとき、集合Pから選んだ要素は、集合Qの要素でもあります。それに対して、集合Qから選んだ要素は、集合Pの要素になるとは限りません。もしかすると、他の集合Rの要素かもしれません。
このような関係にあるとき、集合Pから要素を選べば、それは必然的に集合Qの要素になります。
ですから、集合Qは、集合Pにとって十分ではないけれど、(命題がP⇒Qが成り立つのに)必要な集合です。
また、集合Qには集合Pに属さない要素があります。
ですから、集合Pは、集合Qにとって必要ではないけれど、(命題がP⇒Qが成り立つのに)十分な集合です。
このように集合P,Qの関係をベン図を用いて考えると、それに対応する2つの条件p,qの関係も分かってきます。
包含関係のある大小2つの条件
包含関係のある大小2つの条件では、小条件であれば大条件を必ず満たします。
しかし、小条件以外にも大条件を満たすものがあります。ですから、小条件は、大条件を満たすのに十分であっても、大条件にとって必要な条件ではありません。
それに対して大条件は、小条件であれば結果的に大条件を満たすので、小条件にとって代用できない条件です。つまり大条件は、小条件にとって外せない必要な条件になります。
相手の条件にとって、十分か必要かといった視点で考えてみると判別がつくこともある。
命題「q⇒p 」が真であるときの十分条件・必要条件
先ほどは、命題「p⇒q」が真であるときを考えました。
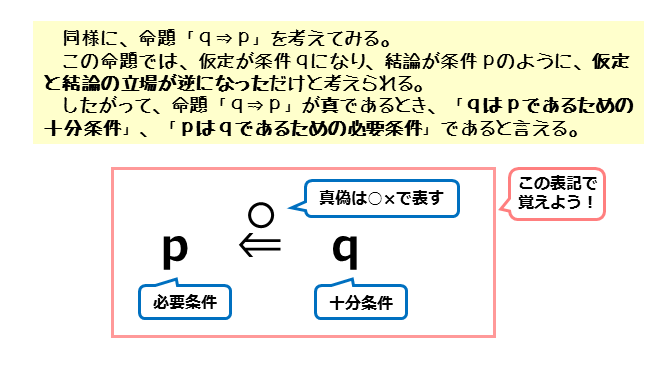
次は、命題「q⇒p」が真であるときを考えます。命題「q⇒p」では、仮定が条件q、結論が条件pです。仮定と結論が逆になっているので注意しましょう。
仮定と結論が逆になっていることから、集合での関係も逆になります。ここに気づけば、十分条件と必要条件の立場も逆になることが分かります。
したがって、命題「q⇒p」が真であるとき、仮定qは結論pであるための十分条件、結論pは仮定qであるための必要条件となります。
次は、必要十分条件や同値についてです。
必要十分条件と同値
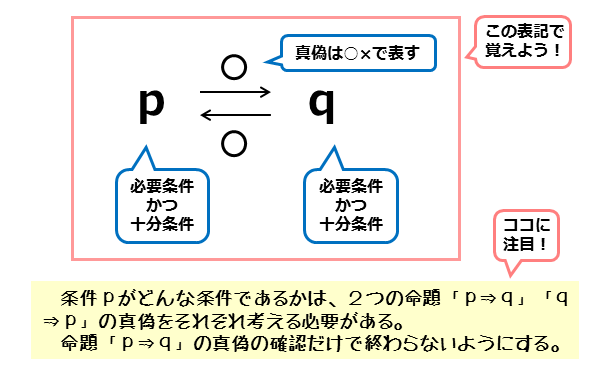
十分条件かつ必要条件である条件
命題「p⇒q」が真であるとき、pはqの十分条件、qはpの必要条件です。pがqの十分条件であることは分かりますが、pがqの必要条件であるかは不明です。これは条件qについても同じです。
しかし、命題「q⇒p(またはp⇐q)」も真であれば、様子が変わります。命題「q⇒p」が真であれば、pはqの必要条件、qはpの十分条件です。
このように、2つの命題「p⇒q」と「q⇒p」がともに真であれば、p,qは互いに十分条件かつ必要条件になります。
一般に、2つの命題がともに真であるとき、「pはqであるための必要十分条件である(同様にqはpであるための必要十分条件である)」と言います。
問題では、命題「p⇒q」が与えられ、pがqにとってどのような条件かを問われます。そのような問題では、2つの命題「p⇒q」と「q⇒p」の真偽を確認しなければなりません。
命題「p⇒q」では、pが条件qの十分条件かそうでないかが分かる。pがqの必要条件かどうかは、命題「q⇒p(またはp⇐q)」で分かる。
同値とは同じ条件ということ
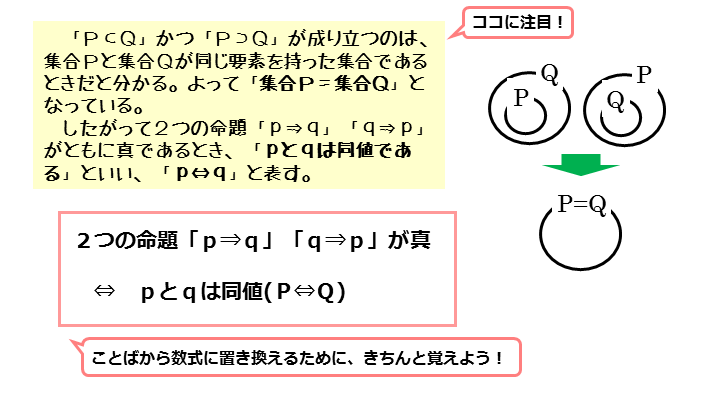
2つの命題「p⇒q」と「q⇒p(またはp⇐q)」がともに真であるとき、「pとqは同値である」とも言います。
このときの条件p,qの関係を集合を使って考えてみましょう。
命題「p⇒q」が真であるとき、集合P,Qの間にはP⊂Qが成り立ちます。
また、命題「q⇒p(またはp⇐q)」が真であるとき、集合P,Qの間にはQ⊂Pが成り立ちます。
このとき、集合P,Qは互いの要素を持ち合います。このような状況が成り立つのは、集合P,Qが全く同じ要素をもつ、言い換えると、P=Qであるときです。
条件p,qがともに必要十分条件になるとき、集合ではその大きさも要素の数もすべて同じになるので、同値であると言います。ちなみに、pとqが同値であることを「p⇔q」と記述します。
次は、十分条件や必要条件を扱った問題を実際に解いてみましょう。