数学２
今回は、平行四辺形の頂点の座標について学習しましょう。ここでは、平行四辺形を作るとき、４つの頂点のうち３つが既知で、残りの頂点の座標を考えます。
図形を扱った問題では、三角形や四角形が題材としてよく用いられます。演習をこなして慣れておきましょう。
平行四辺形の頂点
平行四辺形の名称の有無
平行四辺形の頂点を考える問題では、平行四辺形の名称の有無を確認しておく必要があります。
たとえば、３点Ａ，Ｂ，Ｃの頂点の座標が予め与えられているとします。このとき「平行四辺形ＡＢＣＤ」と言われれば、点Ｄの位置はただ１つに固定されます。図では、反時計回りに頂点Ａ，Ｂ，Ｃ，Ｄと並んでいる平行四辺形だけになります。
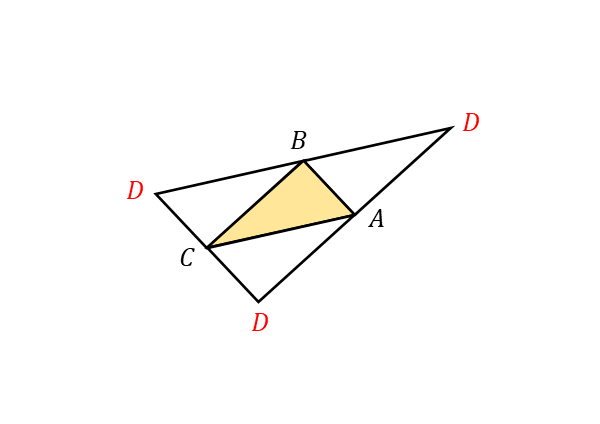頂点Ｄの位置 それに対して「４点Ａ，Ｂ，Ｃ，Ｄが平行四辺形の頂点となるように」と言われれば、点Ｄの位置はただ１つに固定されません。
図では、点Ｄの位置は３通り考えられます。４点で平行四辺形ができていれば、平行四辺形ＡＢＣＤでも良いし、平行四辺形ＡＢＤＣや平行四辺形ＡＤＢＣでも良いわけです。
このことから分かるのは、図形の名称は頂点の並びを示す情報だということです。
図形の名称にはルールがあり、頂点に振ったアルファベットを時計回り、または反時計回りに順番に読むことになっています。このことが分かっていれば、図形の名称が大切な情報だと分かるはずです。
平行四辺形の頂点の求め方
平行四辺形の４つの頂点のうち、３つの座標が与えられているとします。このとき、残りの点の座標を求めるには、平行四辺形の性質を利用します。
平行四辺形の対角線には以下の性質があります。
平行四辺形の対角線
平行四辺形の２本の対角線は、互いに他を二等分する。
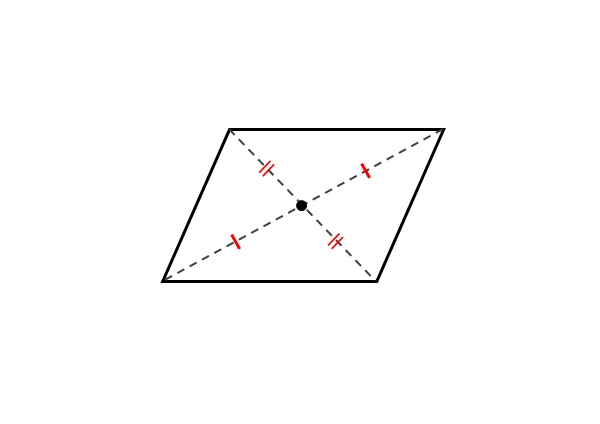平行四辺形の性質 言い換えると、平行四辺形の２本の対角線の中点は一致するということです。ですから、それぞれの対角線で中点を求め、そしてｘ座標どうし、ｙ座標どうしを等号でそれぞれ結べば、方程式を導くことができます。
平行四辺形の頂点の座標を求めてみよう
例題
\begin{align*}
&\text{$3$ 点 $A(5 \ , \ -1) \ , \ B(3 \ , \ 3) \ , \ C(-1 \ , \ -3)$ を頂点とする} \\[ 5pt ]
&\text{平行四辺形の残りの頂点 $D$ の座標を求めよ。}
\end{align*}
例題の解答・解説
問題文を注意深く読みましょう。平行四辺形の頂点にアルファベットが振ってありますが、平行四辺形の名称がありません。つまり、頂点の順序が示されていません。
３点Ａ，Ｂ，Ｃの座標が与えられているので、座標平面に図示してみましょう。そうすれば、点Ｄの位置を予想することができるでしょう。
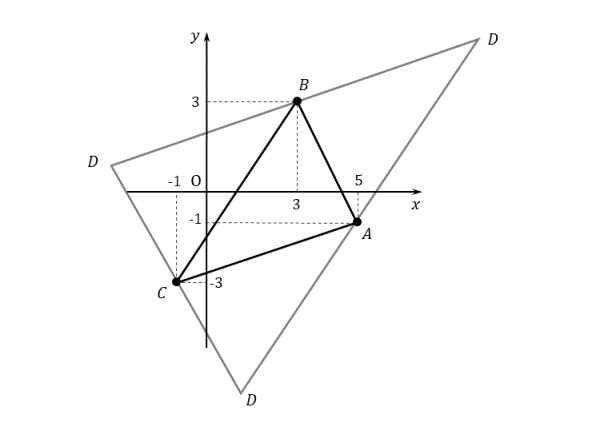例題の作図 図を参考にすれば、点Ｄの候補は３通りあることが予想できます。点Ｄの座標を定義しておき、できる平行四辺形を書き並べます。
例題の解答例 1⃣
\begin{align*}
&\quad A(5 \ , \ -1) \ , \ B(3 \ , \ 3) \ , \ C(-1 \ , \ -3) \\[ 7pt ]
&\text{残りの頂点 $D$ の座標を $(x \ , \ y)$ とする。} \\[ 5pt ]
&\text{平行四辺形の頂点の順序は、次の $3$ つの場合がある。} \\[ 5pt ]
&\quad (i) \ \text{平行四辺形 $ABCD$ } \\[ 5pt ]
&\quad (ii) \ \text{平行四辺形 $ABDC$ } \\[ 5pt ]
&\quad (iii) \ \text{平行四辺形 $ADBC$ }
\end{align*}
それぞれの平行四辺形において、点Ｄの座標を求めます。平行四辺形の対角線の性質を利用します。
まず、平行四辺形ＡＢＣＤの場合です。対角線は、２つの線分ＢＤ，ＡＣです。
例題の解答例 2⃣
\begin{align*}
&\quad A(5 \ , \ -1) \ , \ B(3 \ , \ 3) \ , \ C(-1 \ , \ -3) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&(i) \ \text{平行四辺形 $ABCD$ の場合} \\[ 5pt ]
&\text{線分 $BD$ と線分 $AC$ の中点が一致するので、} \\[ 5pt ]
&\quad \frac{x+3}{2}=\frac{5+(-1)}{2} \\[ 7pt ]
&\quad \frac{y+3}{2}=\frac{(-1)+(-3)}{2} \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad x=1 \\[ 7pt ]
&\quad y=-7
\end{align*}
次に、平行四辺形ＡＢＤＣの場合です。対角線は、２つの線分ＡＤ，ＢＣです。
例題の解答例 3⃣
\begin{align*}
&\quad A(5 \ , \ -1) \ , \ B(3 \ , \ 3) \ , \ C(-1 \ , \ -3) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&(ii) \ \text{平行四辺形 $ABDC$ の場合} \\[ 5pt ]
&\text{線分 $AD$ と線分 $BC$ の中点が一致するので、} \\[ 5pt ]
&\quad \frac{x+5}{2}=\frac{3+(-1)}{2} \\[ 7pt ]
&\quad \frac{y+(-1)}{2}=\frac{3+(-3)}{2} \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad x=-3 \\[ 7pt ]
&\quad y=1
\end{align*}
さいごに、平行四辺形ＡＤＢＣの場合です。対角線は、２つの線分ＣＤ，ＡＢです。
例題の解答例 4⃣
\begin{align*}
&\quad A(5 \ , \ -1) \ , \ B(3 \ , \ 3) \ , \ C(-1 \ , \ -3) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&(iii) \ \text{平行四辺形 $ADBC$ の場合} \\[ 5pt ]
&\text{線分 $CD$ と線分 $AB$ の中点が一致するので、} \\[ 5pt ]
&\quad \frac{x+(-1)}{2}=\frac{5+3}{2} \\[ 7pt ]
&\quad \frac{y+(-3)}{2}=\frac{(-1)+3}{2} \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad x=9 \\[ 7pt ]
&\quad y=5\\[ 7pt ]
&(i) \ , \ (ii) \ , \ (iii) \ \text{より、頂点 $D$ の座標は} \\[ 5pt ]
&\quad (1 \ , \ -7) \ , \ (-3 \ , \ 1) \ , \ (9 \ , \ 5)
\end{align*}
中点の座標の求め方は、図形を扱った問題では頻出なので、しっかりマスターしておきましょう。
中点の座標
\begin{align*}
&\text{$A(x_{1} \ , \ y_{1}) \ , \ B(x_{2} \ , \ y_{2})$ とするとき、} \\[ 5pt ]
&\text{線分 $AB$ の中点の座標は} \\[ 5pt ]
&\quad \left(\frac{x_{1}+x_{2}}{2} \ , \ \frac{y_{1}+y_{2}}{2} \right)
\end{align*}
次は、平行四辺形の頂点の座標を扱った問題を実際に解いてみましょう。
