数学1|図形を扱った入試問題を解いてみよう

今回、紹介する問題は図形問題です。一見して簡単そうに見えますが、意外と難しい問題です。
図形を扱った問題の場合、解ける解けないの差がはっきりするような気がします。やはり慣れが必要かもしれません。
過去問を解いてみよう
過去の入試問題になります。最初は力試しに自力で解いてみることをお勧めします。
問題
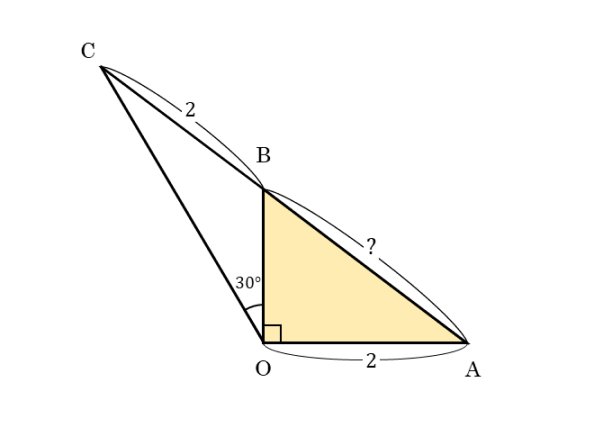
図において
\begin{align*} &\quad \angle {BOC}=30^{\circ} \\[ 7pt ] &\quad OA=BC=2 \end{align*}とするとき、$AB^{\scriptsize{3}}$ を求めよ。
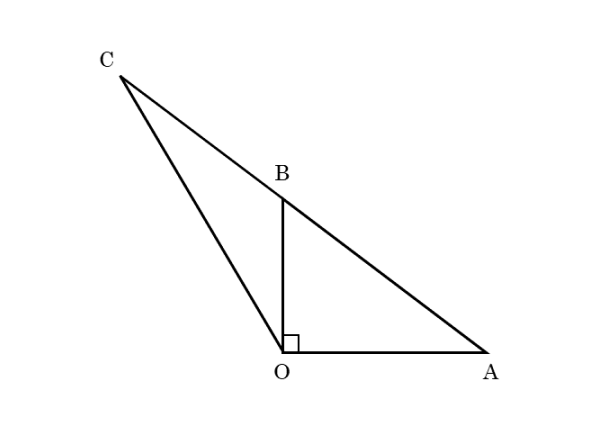
自力で解けない人は、以下の「問題を解く前に」を確認しましょう。
問題を解く前に
方針を決めよう
マーク形式レベルであれば、方針に複数の候補がほとんど出てこないので、問題を読めばすぐに取り掛かれます。
それに対して、記述形式レベル(大学別の個別試験、通称2次試験レベル)になると、方針の候補が1つではない問題が多くなります。そもそも方針自体を立てることが難しい問題も多いでしょう。
そんな問題に対して、方針があやふやなままでは解ききることは困難です。完答は無理でも、部分点を確保するには、答案の中で方針を示す必要があります。
要するに、記述形式レベルを問題を解くには、記述する前に方針をきちんと決めることがとても大切になります。
本問は、図形の辺の長さを求める問題です。辺の長さの求め方としては、主に3つが考えられます。
辺の長さを求めるときに利用するもの
- 三平方の定理
- 相似の関係
- 三角比
与えられた図を観察すると、3つの三角形があることが分かります。△OAB,△OBC,△OACの3つです。
与えられた角の大きさや辺の長さから、相似の関係を利用することはこのままでは無理そうです。三平方の定理か三角比に絞って各三角形を見ていきます。
△OABについて
△OABは∠OAB=90°の直角三角形です。ABの長さを求めるにあたって、真っ先に目に注目する三角形でしょう。
直角三角形なので、三平方の定理を利用できます。三平方の定理から辺の長さを求めるには、少なくとも2辺の長さを必要とします。
残念ながら、長さを与えられたのは、3辺のうちOAだけです。OBの長さが分かれば良いのですが難しそうです。
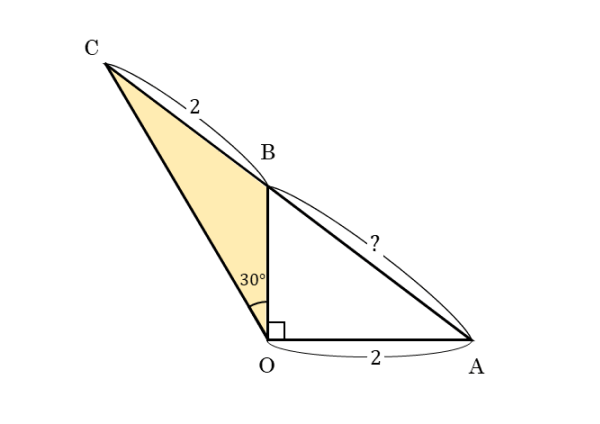
△OBCについて
△OBCは、直角三角形ではありませんが、∠COB=30°の三角形です。
△OBCはABに直接関係するわけではありません。しかし、△OABとOBを共有しています。ですから、余弦定理を利用して、OBの長さを求めたいところです。
余弦定理の式は、1つの内角と3つの辺の関係を表します。もし、内角の大きさを求めるのであれば、3辺の長さが分かっていることが条件です。また、1辺の長さを求めるのであれば、内角の大きさと2辺の長さが分かっていることが条件です。
△OBCにおいて、余弦定理からOBの長さを求めるとすれば、OCの長さが必要になります。残念ながら、長さを与えられたのは、3辺のうちBCだけです。OCの長さが分かれば良いのですが難しそうです。
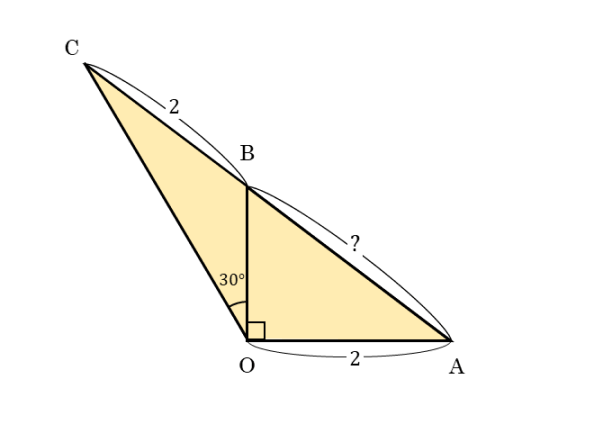
△OACについて
△OACは∠AOC=120°の三角形です。∠AOC=∠AOB+∠BOCが成り立ちます。
ACの長さが分かれば、ABの長さが分かります。しかし、この三角形でもOCの長さが分からないので、余弦定理を利用できません。
このように各三角形を見てみると、どれも1辺の長さの情報が足りない状況になっています。ここから分かるのは、この問題のポイントが「足りない辺の長さをどのようにして得るか」ということです。
また、以上の考察から、ABの長さを求めるのに効率の良さそうな辺の長さは、OCの長さではないかと予想できます。
与えられた角の大きさを活用する
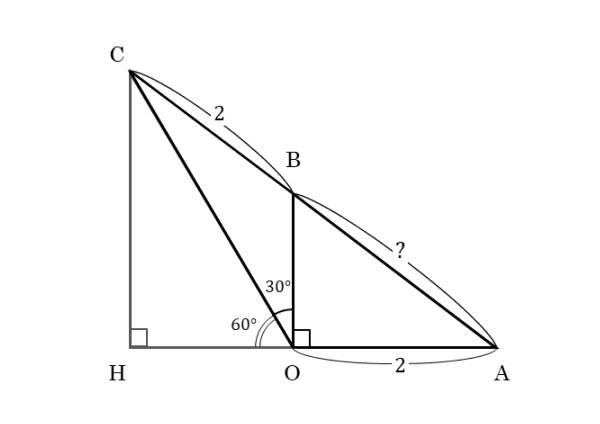
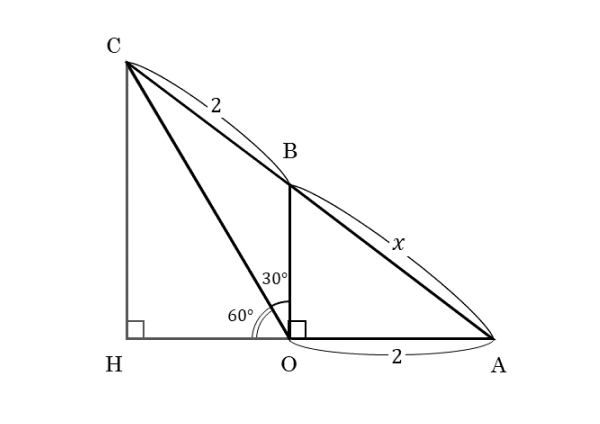
以上の考察を踏まえて、与えられた∠BOCの大きさ(30°)を活用できないかを考えます。頂点Cから直線OAに垂線を下ろし、その足をHとします。
補助線である垂線を使って、新たな△OCHを作ります。△OCHは∠COH=90°の直角三角形です。しかも、∠COH=60°であるので、3辺の比を利用できます。
また、OBとCHは平行なので、平行線と線分の比の関係も利用できます。これを利用すれば、OHの長さをABを用いて表すことができそうです。
OHの長さが決まれば、3辺の比を利用してOCの長さも決まります。これで大まかな方針が決まりました。与えられた30°の使い方に気付けるかどうかで見通しの良さがだいぶ変わります。
問題の解答・解説
求めたいABの長さをxとおき、平行線と線分の比を利用してOHをABで表します。
問題の解答例 1⃣
\begin{align*} \quad AB=x \quad (\gt 0) \end{align*}とおく。
$AB$ と $CH$ は平行であるので
\begin{align*} \quad AB : BC = AO : OH \end{align*}が成り立つ。よって
\begin{align*} \quad x : 2 = 2 : OH \end{align*}より
\begin{align*} \quad OH= \frac{4}{x} \quad \cdots \text{①} \end{align*}直角三角形である△OCHに注目します。3辺の比、または三角比を利用して、OCをABで表します。
問題の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad OH= \frac{4}{x} \quad \cdots \text{①} \end{align*}$\triangle {OCH}$ において
\begin{align*} \quad \angle {COH}=60^{\circ} \end{align*}であるので
\begin{align*} \quad OH=OC \cos {60^{\circ}} \end{align*}よって
\begin{align*} \quad OC=2OH \end{align*}これと①より
\begin{align*} \quad OC=\frac{8}{x} \end{align*}これで念願のOCの長さが決まりました。△OACの3辺の長さは、値こそ分かりませんが、文字を用いて表せるのですべて埋まっています。
また、∠AOC=120°であるので、内角も1つ分かっています。
△OACにおいて余弦定理を利用できる条件が揃いました。余弦定理を利用して、xについての方程式を導き、そして解きます。
問題の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad OC=\frac{8}{x} \end{align*}$\triangle {OAC}$ において、余弦定理より
\begin{align*} \quad AC^{2}=OA^{2}+OC^{2}-2OA \cdot OC \cos {120^{\circ}} \end{align*}よって
\begin{align*} \quad \left(x+2 \right)^{2}=2^{2}+\left( \frac{8}{x} \right)^{2}-2 \cdot 2 \cdot \frac{8}{x} \cdot \left( -\frac{1}{2} \right) \end{align*}これを整理すると
\begin{align*} &\Longleftrightarrow \quad x^{2}+4x+4=4+\frac{64}{x^{2}}+\frac{16}{x} \\[ 7pt ] &\Longleftrightarrow \quad x^{2}+4x=\frac{64}{x^{2}}+\frac{16}{x} \\[ 7pt ] &\Longleftrightarrow \quad x \left(x+4 \right)=\frac{16}{x^{2}} \left(4+x \right) \\[ 7pt ] &\Longleftrightarrow \quad x^{3} \left(x+4 \right)=16 \left( x+4 \right) \quad (\because \ x^{2} \neq 0) \\[ 7pt ] &\Longleftrightarrow \quad x^{3}=16 \quad (\because \ x+4 \neq 0) \end{align*}ここで
\begin{align*} \quad x=AB \end{align*}であるので
\begin{align*} \quad AB^{3}=16 \end{align*}xについての方程式を導いた後は、要領よく変形していきましょう。解答例を見れば大したことではないと分かりますが、実際に解いてみると意外と考えさせられます。
入試レベルの問題では、よく考えないとなかなか解けないものが多いです。思考力が鍛えられるので、日頃から標準レベル以上の問題に積極的に取り組みたいところです。
共通テストでは「思考力・表現力・判断力」を試す問題が多く出題されることが分かっています。そのような問題に対応するためにも、覚えれば解けるような問題よりも、方針をきちんと立てる必要のある問題を多くこなすことが大切です。
Recommended books
大学入試の仕組みが変わり、思考力・表現力・判断力をこれまで以上に問われるようになります。日頃から意識的に取り組むことが大切です。
オススメその1
最初に紹介するのは、河合塾SERIESの『これからの大学入試に必要な数学の「思考力」を鍛える問題集』です。
河合塾数学科の考える「思考力・判断力・表現力」がまとめられています。過去の入試問題を分析し、その中から思考力を養うために経験しておきたい問題を収集してあります。
また、試行調査の問題を参考にした「共通テスト型問題」も収録されています。
オススメその2
2冊目は『総合的研究 記述式答案の書き方ーー数学I・A・II・B』です。数学に苦手意識がなく、将来的に得意科目にしたい人向けです。
『総合的研究』シリーズは、チャート式やフォーカスゴールドなどと並んで有名な参考書で、数学以外の科目もあります。また、電子書籍でも出版されているので、持ち運びに苦労しないのもポイントが高いです。
この本のテーマは《伝える》ことです。私たちは、この本で、数学的に正当な思考・数学的な事実を、どうすれば文章にして他者に伝えられるか、懸命に説明しています。
ちょっとした言葉づかい、論理的な説明の順序、条件と命題の違いの意識、いろいろな文字の立場の理解・・・・・・きっと、読者の皆さんの考えを読み手に《伝える》ために、すぐ役立つはずです。
(中略)数学の答案作りとは、自分と読み手のあいだに小さいながらも数学の世界を築く作業です(抽象的な言い方ですが、数学的に正しい主張とは、常に完結した、バランスの取れた小宇宙です)。
自分の知性と読み手の知性、双方を信頼し、両者の思考をつなぎ、そこに確固たる数学的結論を創造する。この営みは、多くの中高生が考えているより、ずっとやりがいのあるものです。
この本を手に取られたあなたが、この本を通じて答案作成の方法を知り、そのたのしみに触れていただけることを祈ります。
それでは、《伝える》レッスンをはじめましょう!(まえがきより)
著者が異なりますが、こちらも『総合的研究』シリーズです。
オススメその3
『基礎からのジャンプアップノート 数学 記述式答案 書き方ドリル』の方が、数学に苦手意識のある人にとっては『総合的研究』シリーズよりも取り組みやすいかもしれません。
数学Ⅰ+A+Ⅱ+Bの記述力の基礎力を固めるなら、まずはこのドリルから!!
問題編64ページ、別冊解答編32ページ
- 証明問題、場合分けの答案の書き方のコツがわかる
- 「なぞって理解する」書き込みノートだから、わかりやすい答案の書き方が覚えやすい
- 「例(手本)」→「Check!」→「練習問題」 まねる&繰り返すの流れで、記述力UP!
- 別冊「解答編」では、練習問題をくわしく解答
『基礎からのジャンプアップノート』は数学以外の科目にもあります。基礎レベルの内容を扱っており、ページ数も多くありません。日常学習での予習や復習に使い勝手が良いでしょう。