数学Ｂ｜数列を扱った入試問題を解いてみよう

01/14/2023数学Ｂ

問題の解答・解説

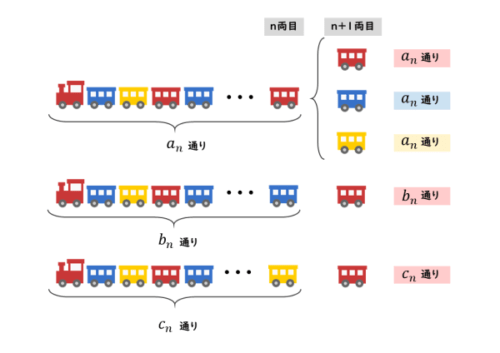
図のように、ｎ両目とｎ＋１両目について考えます。この２両であっても、色の組合せは変わりません。

問題の解答例 1⃣

隣り合った車両の少なくとも一方が赤色となる塗り方をした $n$ 両編成の列車について、最後尾の車両が赤色、青色、黄色であるものをそれぞれ $a_{n} \ , \ b_{n} \ , \ c_{n}$ 通りあるとする。

$n$ 両目が赤色ならば、$n+1$ 両目は赤色、青色、黄色のいずれかであり、$n$ 両目が青色ならば、$n+1$ 両目は赤色、$n$ 両目が黄色ならば、$n+1$ 両目は赤色である。

よって

\begin{align*} \quad \left\{ \begin{array}{l} a_{n+1}=a_{n}+b_{n}+c_{n} \quad \cdots \text{①} \\[ 7pt ] b_{n+1}=a_{n} \\[ 7pt ] c_{n+1}=a_{n} \end{array} \right. \end{align*}

隣り合うｎ両目とｎ＋１両目について、漸化式を導くことができました。これらを連立して解きます。

問題の解答例 2⃣

\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \left\{ \begin{array}{l} a_{n+1}=a_{n}+b_{n}+c_{n} \quad \cdots \text{①} \\[ 7pt ] b_{n+1}=a_{n} \\[ 7pt ] c_{n+1}=a_{n} \end{array} \right. \end{align*}

①から

\begin{align*} \quad a_{n+2}=a_{n+1}+b_{n+1}+c_{n+1} \end{align*}

ここで

\begin{align*} \quad b_{n+1}=a_{n} \ , \ c_{n+1}=a_{n} \end{align*}

より

\begin{align*} \quad a_{n+2}=a_{n+1}+a_{n}+a_{n} \end{align*}

よって

\begin{align*} \quad a_{n+2}-a_{n+1}-2a_{n}=0 \quad \cdots \text{②} \end{align*}

隣接３項間の漸化式②を導くことができました。隣接３項間の漸化式には特性方程式があります。これを利用して変形します。

問題の解答例 3⃣

\begin{align*} &\quad \vdots \\[ 7pt ] &\quad a_{n+2}-a_{n+1}-2a_{n}=0 \quad \cdots \text{②} \end{align*}

②から

\begin{align*} \quad \left\{ \begin{array}{l} a_{n+1}-2a_{n}=-\left(a_{n+1}-2a_{n} \right) \\[ 10pt ] a_{n+1}+a_{n}=2\left(a_{n+1}+a_{n} \right) \end{array} \right. \end{align*}

よって

数列 $\{ a_{n+1}-2a_{n} \}$ は公比 $-1$

数列 $\{ a_{n+1}+a_{n} \}$ は公比 $2$

の等比数列となる。

隣接３項間の漸化式の場合、変形のやり方は２通りあるので注意しましょう。

それぞれの等比数列の一般項を求めます。

問題の解答例 4⃣

\begin{align*} \quad \vdots \end{align*}

よって

\begin{align*} \quad \left\{ \begin{array}{l} a_{n+1}-2a_{n}=\left(a_{2}-2a_{1} \right) \cdot \left(-1 \right)^{n-1} \\[ 7pt ] a_{n+1}+a_{n}=\left(a_{2}+a_{1} \right) \cdot 2^{n-1} \end{array} \right. \end{align*}

ここで

\begin{align*} \quad a_{1}=1 \ , \ a_{2}=3 \end{align*}

であるので

\begin{align*} \quad \left\{ \begin{array}{l} a_{n+1}-2a_{n}=\left(3-2 \cdot 1 \right) \cdot \left(-1 \right)^{n-1} \\[ 7pt ] a_{n+1}+a_{n}=\left(3+1 \right) \cdot 2^{n-1} \end{array} \right. \end{align*}

ここで

\begin{align*} \quad 1=\left(-1 \right)^{2} \ , \ 4=2^{2} \end{align*}

より

\begin{align*} \quad \left\{ \begin{array}{l} a_{n+1}-2a_{n}=\left(-1 \right)^{n+1} \quad \cdots \text{③} \\[ 10pt ] a_{n+1}+a_{n}=2^{n+1} \quad \cdots \text{④} \end{array} \right. \end{align*}

各数列の一般項が分かったので、これらからａ_n+1 を消去します。

問題の解答例 5⃣

\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \left\{ \begin{array}{l} a_{n+1}-2a_{n}=\left(-1 \right)^{n+1} \quad \cdots \text{③} \\[ 10pt ] a_{n+1}+a_{n}=2^{n+1} \quad \cdots \text{④} \end{array} \right. \end{align*}

④－③より

\begin{align*} \quad 3a_{n}=2^{n+1}-\left(-1 \right)^{n+1} \end{align*}

よって

\begin{align*} \quad a_{n}=\frac{1}{3} \left\{ 2^{n+1}-\left(-1 \right)^{n+1} \right\} \quad \cdots \text{⑤} \end{align*}

求めたい場合の数は、隣り合った車両の少なくとも一方が赤色となるような色の塗り方です。ですから、ａ_n+1 の式を導きます。

問題の解答例 6⃣

\begin{align*} &\quad a_{n+1}=a_{n}+b_{n}+c_{n} \quad \cdots \text{①} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad a_{n}=\frac{1}{3} \left\{ 2^{n+1}-\left(-1 \right)^{n+1} \right\} \quad \cdots \text{⑤} \end{align*}

求める場合の数は、①，⑤より

\begin{align*} \quad a_{n}+b_{n}+c_{n}=a_{n+1} \end{align*}

したがって

\begin{align*} \quad \frac{1}{3} \left\{ \ 2^{\left(n+1 \right)+1}-\left(-1 \right)^{\left(n+1 \right)+1} \ \right\}=\frac{1}{3} \left\{ 2^{n+2}-\left(-1 \right)^{n+2} \right\} \end{align*}

漸化式さえ導くことができれば、あとは計算ミスをしないように丁寧に変形していくだけです。

しかし、最初で躓くと、なかなか手の進まない問題だったかもしれません。

場合の数についての漸化式を導くために、１両目と２両目、２両目と３両目……と具体例を考え、そこから規則性を探すことが必要でした。

具体例を考えたのは、場合の数を求めるためではなく、規則性を探すためです。

入試レベルの問題では、具体例が少ないと、方針を上手く立てられません。気付きを得るまでは、途中で諦めずに具体例を挙げ続けることが大切です。

具体例を挙げていってもなかなか解けず、長く考えさせられることが多いでしょう。そういう意味では、入試の過去問は思考力を鍛えることにとても役立ちます。

できることなら日頃から標準レベル以上の問題に積極的に取り組みたいところです。

共通テストでは「思考力・表現力・判断力」が試される問題が多く出題されることが分かっています。

そのような問題に対応するためにも、覚えれば解けるような問題よりも、じっくり考えて解く必要がある問題を多くこなすことが大切です。

隣接３項間の漸化式

隣接３項間の漸化式とその特性方程式をまとめると以下の通りです。

隣接３項間の漸化式

\begin{align*} \quad pa_{n+2}+qa_{n+1}+ra_{n}=0 \end{align*}

について

\begin{align*} \quad px^{2}+qx+r=0 \end{align*}

を特性方程式と言い、この方程式の解を

\begin{align*} \quad \alpha \ , \ \beta \end{align*}

とする。

ただし、$\alpha \neq 1$ かつ $\beta \neq 1$ かつ $\alpha \neq \beta$ のとき

\begin{align*} \quad \left\{ \begin{array}{l} a_{n+1}-\alpha a_{n}=\beta \left(a_{n+1}-\alpha a_{n} \right) \\[ 7pt ] a_{n+1}-\beta a_{n}=\alpha \left(a_{n+1}-\beta a_{n} \right) \end{array} \right. \end{align*}

を導くことができる。

数列 $\{ a_{n+1}-\alpha a_{n} \}$ の一般項は

\begin{align*} \quad a_{n+1}-\alpha a_{n}= \left( a_{2}-\alpha a_{1} \right) {\beta}^{n-1} \end{align*}

数列 $\{ a_{n+1}-\beta a_{n} \}$ の一般項は

\begin{align*} \quad a_{n+1}-\beta a_{n}= \left( a_{2}-\beta a_{1} \right) {\alpha}^{n-1} \end{align*}

$2$ つの一般項の式から $a_{n+1}$ を消去して、数列 $a_{n}$ の一般項を求める。

他には

$\alpha \ , \ \beta$ のうち一方が $1$ のとき

$\alpha = \beta$ かつ $\alpha \neq 1$ かつのとき

がありますが、上の場合よりも易しくなります。