確率|確率の基本性質について

前回、確率に関わる用語やその定義を学習したので、今回は確率の基本性質について学習しましょう。
基本性質と言うくらいなので、この性質を使いながら色々な事柄が起こる確率を求めていきます。確実に使えるようにしておきましょう。
なお、記事の画像が見辛いときはクリックすると拡大できます。
確率の基本的な性質
確率を求める式は基本的に1つだけです。ある事象が起こる確率であればこの式で求めることができるので、それほど難しくはありません。
確率
このときの事象 $A$ が起こる確率 $P(A)$
\begin{align*} P(A) = \frac{\text{事象 $A$ が起こる場合の数}}{\text{起こりうるすべての場合の数}} \end{align*}1つの事象が起こる確率であれば、上述の式で簡単に求めることができます。
しかし、複数の事象が起こる確率となると、単純にこの式を使って求めることはできません。事象どうしの関係を考えないといけないからです。ここを間違うと、正しい確率を求めることができないので注意が必要です。
積事象・和事象、排反、余事象
まず用語を確認しましょう。最初は「積事象」と「和事象」です。
- 積事象:2つの事象A,Bについて、AとBがともに起こる事象のこと。A⋂Bと表す。
- 和事象:2つの事象A,Bについて、AまたはBが起こる事象のこと。A⋃Bと表す。
「共通部分」や「和集合」から呼び名が変わったと捉えると、理解に苦しむことはないでしょう。
このような事象について、積事象A⋂Bが起こる確率をP(A⋂B)、和事象A⋃Bが起こる確率をP(A⋃B)と表します。
2つの事象がともに起こることがあるとき
積事象と和事象が起こる確率について、一般に以下のような関係が成り立ちます。
積事象と和事象が起こる確率の関係 1⃣
\begin{align*} P \left(A \cup B \right) = P \left(A \right) + P \left(B \right) – P \left(A \cap B \right) \end{align*}和事象を求めるには、単純にそれぞれの事象が起こる確率を足せば良いわけではありません。それぞれの事象がともに起こる確率(積事象が起こる確率)を除外しなくてはなりません。
2つの事象がともに起こることがないとき
上の式では、2つの事象がともに起こることを踏まえています。しかし、2つの事象A,Bがともに起こることがない(同時に起こらない)ときもあります。それが「排反」という関係です。
排反
事象A,Bが同時に起こらないこと。このとき、AとBは互いに排反(事象)であると言う。
2つの事象A,Bが互いに排反であれば、A⋂B=∅であるので、先ほどの式は以下のようになります。
積事象と和事象が起こる確率の関係 2⃣
$2$ つの事象 $A \ , \ B$ が互いに排反であるとき
\begin{align*} \quad A \cap B = \varnothing \end{align*}となるので
\begin{align*} \quad P \left( A \cap B \right) = 0 \end{align*}である。よって
\begin{align*} \quad P \left(A \cup B \right) = P \left(A \right) + P \left(B \right) \quad \text{(加法定理)} \end{align*}A⋂B=∅であれば、積事象A⋂Bの要素はありません。このとき、積事象A⋂Bが起こる場合の数は0となるので、その確率はP(A⋂B)=0です。
このことから、和事象A⋃Bが起こる確率は、2つの事象A,Bがそれぞれ起こる確率の和だけで表されます。この式を加法定理と言うことがあります。
特定の事象が起こらないときの事象
さいごに「余事象」です。余事象は補集合をイメージすると分かりやすいでしょう。
余事象
事象Aについて、事象Aが起こらない事象のこと。事象Aの余事象を $\overline{A}$ と表す。
事象Aの余事象 $\overline{A}$ が起こる確率 $P(\bar{A})$ は以下のように表せます。
事象Aの余事象が起こる確率
事象 $A$ の余事象を $\overline{A}$ とすると
\begin{align*} \quad P( \ \overline{A} \ ) = 1 \ – P(A) \end{align*}これまでをまとめると以下のようになります。
次は積事象や和事象を具体例で考えてみましょう。
積事象と和事象の関係式を使ってみよう
次の確率を求めてみましょう。
例題1
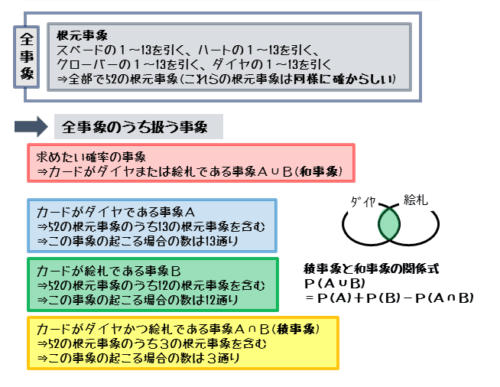
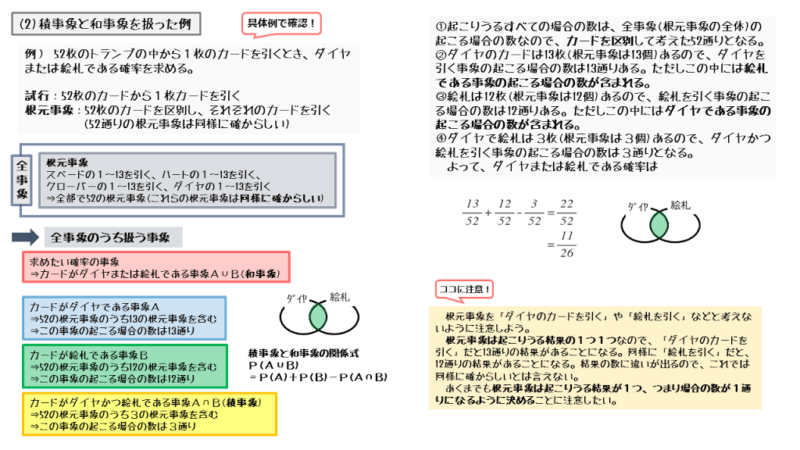
52枚のトランプの中から1枚のカードを引くとき、ダイヤまたは絵札である確率
根元事象を正しく定めよう
試行は「52枚のトランプの中から1枚のカードを引く」となります。次は事象についてですが、少し注意が必要です。
問題文には「ダイヤのカードを引く」や「絵札を引く」という文言がありますが、これらは根元事象ではないことに気を付けましょう。
これらはあくまでも事象の1つであって、根元事象となる事象ではありません。「ダイヤのカードを引く」や「絵札を引く」といった事象では、枚数が複数(結果が複数)あったり、枚数に違い(偏り)があったりして、同じ程度に起こると期待できないからです。
同じ程度に起こると期待できる根元事象は、必ず1通りの結果を要素にもつ事象です。そのことに注意して根元事象を定めましょう。
トランプなどのカードを引く場合の確率では、数字や絵柄で考えずに、カードをすべて区別して扱います。カードの数字や絵柄にこだわらずに1枚を引くとなれば、同じ程度に起こると期待できます。
以上のことから、根元事象は「区別した52枚のカードをそれぞれ引く」となり、52個の根元事象があることになります。また、全事象は、52個の根元事象をまとめた事象です。
52枚のトランプの中から1枚のカードを引くときの根元事象
$\spadesuit$ の $1$ を引く事象
$\spadesuit$ の $2$ を引く事象
$\quad \vdots$
$\diamondsuit$ の $1$ を引く事象
$\diamondsuit$ の $2$ を引く事象
$\quad \vdots$
$\clubsuit$ の $1$ を引く事象
$\clubsuit$ の $2$ を引く事象
$\quad \vdots$
$\heartsuit$ の $1$ を引く事象
$\heartsuit$ の $2$ を引く事象
$\quad \vdots$
全部で $52$ 個の根元事象があり、これらは同じ程度に起こると期待できる。
根元事象を定めるとき、数字や絵柄にかかわらず、カードの1枚1枚を区別しよう。
根元事象を定めたところで問われている確率を求めます。
事象の要素を数え上げよう
起こりうるすべての場合の数は、全事象の要素の個数から52通りです。
ダイヤまたは絵札である事象は、ダイヤである事象と絵札である事象の和事象です。根元事象をきちんと定めてあるので、ダイヤである事象と絵札である事象を分けて考えることができます。
ダイヤのカードは13枚あるので、ダイヤである事象は13個の根元事象が含みます。これよりダイヤである事象が起こる場合の数は13通りです。
ダイヤである事象
$\diamondsuit$ の $1$ を引く事象
$\diamondsuit$ の $2$ を引く事象
$\quad \vdots$
$\diamondsuit$ の $11$ を引く事象
$\diamondsuit$ の $12$ を引く事象
$\diamondsuit$ の $13$ を引く事象
全部で $13$ 個の根元事象を含む事象
同様にして、絵札のカードは12枚あるので、絵札である事象は12個の根元事象を含みます。これより絵札である事象が起こる場合の数は12通りです。
絵札である事象
$\spadesuit$ の $11$ を引く事象
$\spadesuit$ の $12$ を引く事象
$\spadesuit$ の $13$ を引く事象
$\diamondsuit$ の $11$ を引く事象
$\diamondsuit$ の $12$ を引く事象
$\diamondsuit$ の $13$ を引く事象
$\clubsuit$ の $11$ を引く事象
$\clubsuit$ の $12$ を引く事象
$\clubsuit$ の $13$ を引く事象
$\heartsuit$ の $11$ を引く事象
$\heartsuit$ の $12$ を引く事象
$\heartsuit$ の $13$ を引く事象
全部で $12$ 個の根元事象を含む事象
2つの事象が互いに排反かどうかを確認しよう
2つの事象が起こる場合の数を求めたら、2つの事象が互いに排反であるかどうかを確認します。
ダイヤかつ絵札であるカードが3枚あるので、ダイヤである事象と絵札である事象は同時に起こる場合があります。
ダイヤかつ絵札である事象
$\diamondsuit$ の $11$ を引く事象
$\diamondsuit$ の $12$ を引く事象
$\diamondsuit$ の $13$ を引く事象
全部で $3$ 個の根元事象を含む事象
2つの事象は互いに排反ではないので、積事象であるダイヤかつ絵札である事象が存在します。
ダイヤかつ絵札のカードは3枚あるので、ダイヤかつ絵札である事象は3個の根元事象を含みます。ですから、この事象が起こる場合の数は3通りです。
ベン図を利用すると2つの事象の関係をイメージしやすくなります。
確率を求めよう
以上の考察をもとにして、ダイヤまたは絵札である事象が起こる確率を求めます。
例題1の解答例
$52$ 枚のトランプから $1$ 枚を引く。
このとき、場合の数は全部で $52$ 通り。
また、ダイヤ、絵札、ダイヤかつ絵札である場合の数は
ダイヤである場合の数 … $13$ 通り
絵札である場合の数 … $12$ 通り
ダイヤかつ絵札である場合の数 … $3$ 通り
したがって、ダイヤまたは絵札である確率は
\begin{align*} \quad \frac{13}{52} + \frac{12}{52} – \frac{3}{52} &= \frac{13+12-3}{52} \\[ 7pt ] &= \frac{22}{52} \\[ 7pt ] &= \frac{11}{26} \end{align*}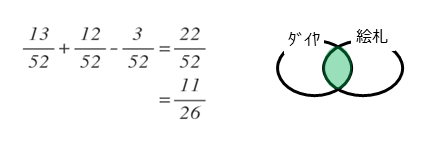
左辺は積事象と和事象の関係式です。右辺は1つの分数にまとめただけですが、確率を求めるときの基本的な式です。
ここで、分子に注目すると、ダイヤまたは絵札である場合の数になっていることが分かります。このことから、確率の求め方は2通りあることが分かります。
確率の求め方
- 求めたい事象が起こる場合の数を求め、確率の式に代入する。
- 各事象の確率を求め、積事象と和事象の関係式で求める。(例題の解答例)
場合の数を使って確率を求めるとき
\begin{align*} P(A \cup B) = \frac{\text{事象 $A \cup B$ が起こる場合の数}}{\text{起こりうるすべての場合の数}} \end{align*}積事象と和事象を使って確率を求めるとき
長い解説になりましたが、最初なのでできるだけ丁寧に説明しました。慣れてくるとほとんどは省略して解くことになります。しかし、基本的な流れを押さえておくことは大切です。
確率を求めるときの基本的な流れ
- 根元事象(要素)を定める
- それらを含む事象(部分集合)や場合の数(要素の個数)を求める
- 確率を求める
積事象と和事象のポイントをまとめると以下のようになります。
次は排反(排反事象)を具体例で考えてみましょう。