2次関数|2次方程式の解法について

今回は、2次方程式の解法について学習しましょう。中学で扱った2次方程式では、そのほとんどが乗法公式を利用した因数分解で解くことができました。
しかし、高校数学では、乗法公式では因数分解のできない式の方が多くなります。もちろん、乗法公式を利用して因数分解できる式もありますが、たすき掛けを利用する場合が多いです。
全体的に扱う式が複雑になるので、式をよく観察して、どのような解法で解を求めれば良いのか判断できるようになりましょう。
2次方程式の解法は2パターン
方程式とは1つ以上の変数を含む等式のことです。この方程式のうち、2次の多項式を扱ったものを2次方程式と言います。
2次方程式の解法には2パターンあります。
2次方程式の解法
- 因数分解して解を求める
- 解の公式を使って解を求める
式を見てすぐに判断できるようになりましょう。
2次方程式を因数分解で解く
2次方程式を因数分解するとき、その方法には2通りあります。
因数分解の方法は2通り
- 共通因数でくくる因数分解
- 乗法公式を利用した因数分解
(2次式)=0という2次方程式を因数分解すると、左辺の2次式は因数の積の形で表されます。この積は右辺が0であることから、因数のいずれかは必ず0になります。
因数分解した後に等式の性質を利用することで、解を求めることができるようになります。
「方程式は左辺と右辺が等しい」という等式の性質を利用。
たとえば、2次方程式をたすき掛けで因数分解すると、左辺が1次式の積で表されます。
左辺の2次式を1次式の積に因数分解
\begin{align*} \quad ac{x}^{2} +\left(ad + bc \right)x +bd &=0 \\[ 7pt ] \left(ax+b \right) \left(cx+d \right) &=0 \end{align*}左辺は $2$ つの $1$ 次式 $ax+b \ , \ cx+d$ の積で表される。
等式の性質から、左辺は右辺と等しいので0になるはずです。左辺の積が0になるということは、1次式ax+b,cx+dのどちらかは必ず0にならなければなりません。
このことから、以下のような等式を2つ導くことができます。
等式の性質から新たな方程式を導出
\begin{align*} \quad \left(ax+b \right) \left(cx+d \right) =0 \end{align*}等式の性質から
\begin{align*} \quad ax+b=0 \end{align*}または
\begin{align*} \quad cx+d =0 \end{align*}が成り立つ。これらを解くと
\begin{align*} \quad x=-\frac{b}{a} \end{align*}または
\begin{align*} \quad x=-\frac{d}{c} \end{align*}よって、与式の解は
\begin{align*} \quad x=-\frac{b}{a} \ , \ -\frac{d}{c} \end{align*}2次方程式を因数分解して等式の性質を利用すると、1次方程式を導くことができます。これらを変数xについて解いた結果が2次方程式の解です。
どちらの1次式の値も0になりうるので「または」の関係。「集合と論理」の単元でも問われる知識。
因数分解での解法をまとめると以下のようになります。
2次方程式を解の公式で解く
因数分解による解法は、等式の性質から解を求めました。それに対して、解の公式を利用した解法は、2次方程式の係数や定数項を利用します。
因数分解よりも直接的な解法なので、式変形に自信がなくても解を求めることができるのが利点です。
解の公式は以下のようになります。
2次方程式の解の公式
$2$ 次方程式
\begin{align*} \quad a{x}^{2} +bx +c =0 \end{align*}について、この $2$ 次方程式の解は
\begin{align*} \quad x = \frac{-b \pm \sqrt{{b}^{2}-4ac}}{2a} \end{align*}の右辺に $a \ , \ b \ , \ c$ の値を代入することで求めることができる。
解の公式を見て分かるように、係数a,bや定数項cの値を用いることによって解(変数xの値)を一気に求めることができます。
高校数学では、解の公式の応用版もあります。上手に使い分けると、計算がラクになります。
解の公式で解を求めると、約分が必要なときがあります。
このようなときは基本的な解の公式ではなく、応用版を使うと約分なしで解を求めることができます。
基本版と応用版の使い分けは、1次の項の係数が偶数かどうかで判断します。
以上のように2通りの方法で、2次方程式を解くことができます。
基本的には、与えられた式に応じて解き方を使い分ける方針の方が良いでしょう。式の扱いに慣れるには、解の公式よりも因数分解の方が適切だからです。
まずは因数分解できないかを考えよう。解の公式は最終手段で。
解の公式を導出してみよう
ところで、解の公式はどのように導出されるのでしょうか?
分かれば大したことではないのですが、導出するにはこれまでの知識を活用する必要があります。少し面倒ですが、公式の導出にチャレンジしてみましょう。
解の公式の導出には平方完成を利用します。
平方完成は、2次関数ではお馴染みの変形です。この平方完成を利用すると、変数xについて解くことができます。
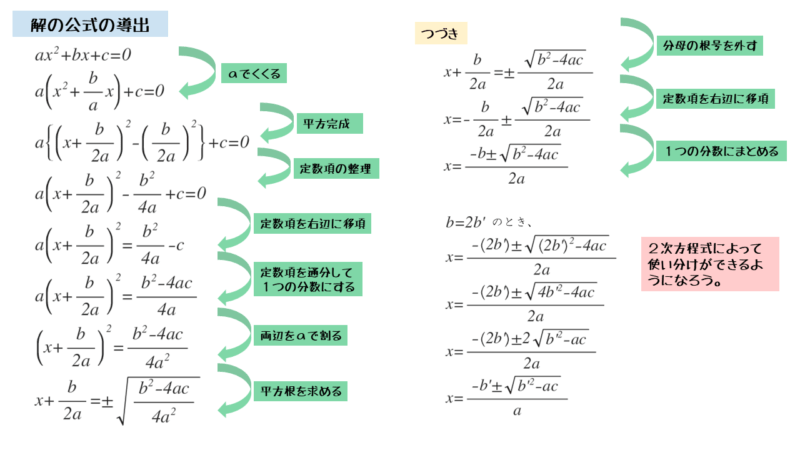
解の公式の導出
\begin{align*} a{x}^{2}+bx+c &= 0 \\[ 7pt ] a\left({x}^{2}+\frac{b}{a} x \right) +c &= 0 \\[ 7pt ] a\left\{ \left(x+\frac{b}{2a} \right)^{2}-\frac{{b}^{2}}{4{a}^{2}} \right\} +c &= 0 \\[ 7pt ] a{\left(x+\frac{b}{2a} \right)}^{2}-\frac{{b}^{2}}{4a} +c &= 0 \\[ 7pt ] a{\left(x+\frac{b}{2a} \right)}^{2}-\frac{{b}^{2}-4ac}{4a} &= 0 \\[ 7pt ] a{\left(x+\frac{b}{2a} \right)}^{2} &= \frac{{b}^{2}-4ac}{4a} \\[ 7pt ] {\left(x+\frac{b}{2a} \right)}^{2} &= \frac{{b}^{2}-4ac}{4{a}^{2}} \\[ 7pt ] x+\frac { b }{ 2a } &= \pm \frac{\sqrt {{b}^{2}-4ac}}{2a} \\[ 7pt ] x &= -\frac{b}{2a} \pm \frac{\sqrt{{b}^{2}-4ac}}{2a} \\[ 7pt ] x &= \frac{-b \pm \sqrt{{b}^{2}-4ac}}{2a} \end{align*}また、$b=2b’$ のとき
\begin{align*} \quad x &= \frac{-2b’ \pm \sqrt{\left(2b’ \right)^{2}-4ac}}{2a} \\[ 7pt ] &= \frac{-2b’ \pm \sqrt{4{b’}^{2}-4ac}}{2a} \\[ 7pt ] &= \frac{-2b’ \pm \sqrt{4\left({b’}^{2}-ac \right)}}{2a} \\[ 7pt ] &= \frac{-2b’ \pm 2\sqrt{{b’}^{2}-ac}}{2a} \\[ 7pt ] &= \frac{-b’ \pm \sqrt{{b’}^{2}-ac}}{a} \end{align*}決して難しいわけではありません。丁寧に変形していけば、きちんと導出することができます。
特に理系志望ならば理系科目を得点源にしたいところです。そのためにも、公式を自分で導出できるようにしておくべきでしょう。
解の公式に限らず、公式の導出ではこれまでに学習してきたことを利用します。そのおかげで知識の定着度合いを確認できたり、他の単元との関わりに気付けたりします。
上手な式の扱い方も身に付けることができるので、受ける恩恵が多いのが公式の導出です。
入試レベルになると、係数や定数項に文字を含む整式を扱うことになる。意外と複雑な式を扱うので、日頃から式の扱いに慣れておこう。
2次方程式の解の意味を考えてみよう
2次方程式の解き方については中学でも学習しているので、ある程度は問題ないかと思います。ここでは、2次方程式を解いて得られる解について考えてみましょう。
2次方程式やその解は、ただの計算問題やその答えだけではありません。たとえば、問題で与えられた関係を数式化したものだったり、個数や長さをもつ数量であったりします。
2次方程式やその解にはそれなりに意味があるということです。では、関数やグラフとの関係はどうでしょうか。
2次方程式が関数やグラフと関係するのは、関数の式においてy=0のときです。
このときの2次方程式は、グラフとx軸との交点(共有点と言う)について考えている式です。ですから、この場合の解は、グラフとx軸との共有点のx座標になります。
2次方程式と関数やグラフとの関係
- (2次方程式)=(関数の式においてy=0のときの式)
- (2次方程式を解く)=(グラフとx軸との共有点のx座標を求める)
- (2次方程式の解)=(グラフとx軸との共有点のx座標)
このように2次方程式は関数やグラフと密接な関係があるので、2次方程式を単独で解くような問題よりも、関数やグラフの問題の中で解くことの方が多くなります。
ですから、2次方程式に出会ったら、ただの計算ではなく、関数やグラフとの関係を意識しながら扱いましょう。
2次方程式の解についてまとめると以下のようになります。
次は、2次方程式を実際に解いてみましょう。
2次方程式に関する問題を解いてみよう
次の問題を解いてみましょう。
式を良く観察して方針を立ててから解きましょう。
問1の解答・解説
問1
次の $2$ 次方程式を解け。
\begin{align*} \quad 2x^{2}-x-1=0 \end{align*}左辺は3項からなる2次式です。このような2次式の場合、乗法公式による因数分解か、解の公式かの二択になります。
問1では、左辺をたすき掛けで因数分解できるので、解の公式を使わずに解きます。
問1の解答例 1⃣
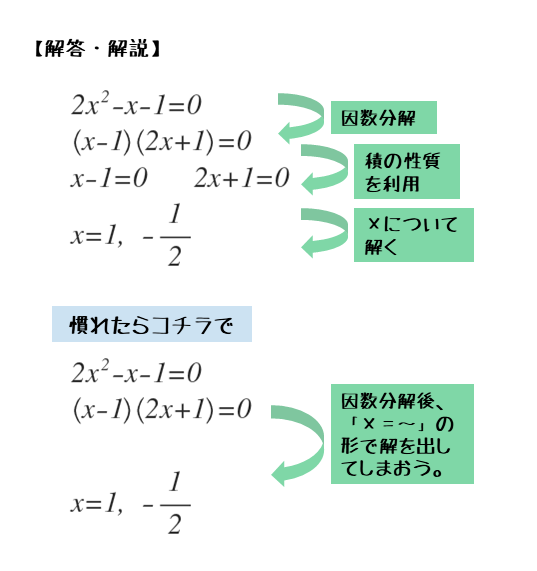
\begin{align*} \quad 2x^{2}-x-1 &=0 \\[ 7pt ] \left(x-1 \right)\left(2x+1 \right) &=0 \end{align*}左辺の2次式を因数分解すると、1次式どうしの積の形になります。
等式の性質を利用して、新たな方程式を導出して解を求めます。
問1の解答例 2⃣
\begin{align*} \quad &\vdots \\[ 7pt ] \quad \left(x-1 \right) &\left(2x+1 \right) =0 \end{align*}等式の性質から
\begin{align*} \quad x-1=0 \ \text{または} \ 2x+1=0 \end{align*}これらを解くと
\begin{align*} \quad x=1 \ \text{または} \ x=-\frac{1}{2} \end{align*}よって、求める解は
\begin{align*} \quad x=-\frac{1}{2} \ , \ 1 \end{align*}たすき掛けに慣れていれば、中学レベルとほとんど変わりません。解答例では、「または」という文言を用いて丁寧に記述しましたが、慣れてくるとほぼ記述されなくなります。
問1のポイントと解答例をまとめると以下のようになります。
たすき掛けに慣れてきたら、暗算で因数分解できるようになろう。計算はスピード感が大切。
問2の解答・解説
問2
次の $2$ 次方程式を解け。
\begin{align*} \quad 2x^{2}+5x+1=0 \end{align*}問1と同じように、左辺は3項からなる2次式です。しかし、今回はたすき掛けでは因数分解できないようです。
問2では、伝家の宝刀「解の公式」で解を求めます。
解の公式
$2$ 次方程式 $a{x}^{2}+bx+c=0$ の解は
\begin{align*} \quad x = \frac{-b \pm \sqrt{{b}^{2}-4ac}}{2a} \end{align*}与式と公式を見比べて、2次式の係数や定数項の対応関係を把握します。
対応関係が分かったら、公式の右辺に対応する数を代入します。代入では符号ミスが多いので気を付けましょう。
問2の解答例 1⃣
与式と公式の対応関係を調べると
\begin{align*} \quad a{x}^{2}+bx+c &=0 \\[ 7pt ] \quad 2x^{2}+5x+1 &=0 \end{align*}より
\begin{align*} \quad a = 2 \ , \ b = 5 \ , \ c = 1 \end{align*}これらを解の公式に代入すると
\begin{align*} \quad x = \frac{-5 \pm \sqrt{{5}^{2}-4 \cdot 2 \cdot 1}}{2 \cdot 2} \end{align*}右辺を整理して
\begin{align*} \quad x = \frac{-5 \pm \sqrt{17}}{4} \end{align*}与式と公式の対応関係を正しく把握することが大切です。
問2のポイントと解答例をまとめると以下のようになります。
初めのうちは公式を覚えるために、暗算せずに数に置き換えて解こう。また、-bのところで符号ミスをしやすいので気を付けよう。
問3の解答・解説
問3
次の $2$ 次方程式を解け。
\begin{align*} \quad 3x^{2}+2x-2=0 \end{align*}問3の式も因数分解できないので、解の公式を使って解きます。ただし、1次の項の係数が偶数なので、解の公式の応用版を使います。
解の公式
$2$ 次方程式 $a{x}^{2}+bx+c=0$ の解は
\begin{align*} \quad x = \frac{-b \pm \sqrt{{b}^{2}-4ac}}{2a} \end{align*}また、$b=2b’$ のとき
\begin{align*} \quad x = \frac{-b’ \pm \sqrt{{b’}^{2}-ac}}{a} \end{align*}与式と公式を見比べて、2次式の係数や定数項の対応関係を把握します。
対応関係が分かったら、公式の右辺に対応する数を代入します。代入では符号ミスが多いので気を付けましょう。
問3の解答例 1⃣
与式と公式の対応関係を調べると
\begin{align*} \quad a{x}^{2}+bx+c &=0 \\[ 7pt ] \quad 3x^{2}+2x-2 &=0 \end{align*}より
\begin{align*} &\quad a = 3 \ , \ b = 2 \ \left(= 2 \cdot 1 \right) \ , \\[ 7pt ] &\quad c = -2 \end{align*}これらを解の公式に代入すると
\begin{align*} \quad x = \frac{-1 \pm \sqrt{{1}^{2}-3 \cdot \left(-2 \right)}}{3} \end{align*}右辺を整理して
\begin{align*} \quad x = \frac{-1 \pm \sqrt{7}}{3} \end{align*}基本的な公式と比べて小さな数で計算できるようになり、計算量が格段に減ります。
ただし、もとの公式と変わる部分に注意しないと計算ミスをします。演習をこなして使いこなせるレベルまで仕上げておきましょう。
問3のポイントと解答例をまとめると以下のようになります。
解の公式では、bの値を代入するときが一番ミスが多くなります。応用版では特にミスしやすくなるので、さらに気を付けましょう。
そうは言っても、使いながら覚えていくのが一番効率が良いので、計算ミスを恐れずにどんどん使っていきましょう。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学2・Bや数学3では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
オススメその1『合格る計算数学1・A・2・B』
我流に陥らないために、「へたな方法」や「いまいちな方法」なども紹介されています。自分の計算のやり方が良いのか悪いのかを客観的に把握できるのがとても良いと思います。
特長
- 「例題」による計算の着眼点(コツ)の解説と習得。「類題」の演習で計算力の定着。
- 「正しい方法」に加えて「へたな方法」「いまいちな方法」の紹介。比較で違いを把握。
- 「ここがツボ!」や「重要ポイントチェック」でポイントを素早く確認。
- 「暗算すべきところ」「できれば暗算してほしいところ」が明確にわかる。
オススメその2『鉄緑会 基礎力完成 数学Ⅰ・A+Ⅱ・B』
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度、頭の中を整理しよう
- 2次方程式の解法は、因数分解または解の公式による解法の2つ。
- 因数分解による解法は、等式や積の性質を利用して求める。
- 解の公式による解法は、2次式の係数や定数項を利用して求める。
- 1次の項の係数が偶数のときなら、簡略化した解の公式を利用できる。