2次関数|2次不等式の解法について(応用編)

2次不等式の解法の基本について学習したので、次は応用編を学習しましょう。
応用編では、2次関数のグラフとx軸との共有点が1個または0個のときの解法になります。
このような2次不等式を解く場合、グラフを図示しないと解を間違う可能性が高くなります。
グラフを図示することの大切さについては何度も言及していますが、その重要性が分かるような問題ではないかと思います。
2次不等式の解法では、グラフとx軸との共有点の個数がポイント
おさらいになりますが、2次不等式の解法の手順は基本的に以下のようになります。
2次不等式の解法の手順
- 2次不等式を2次関数と値域に置き換える
- 2次関数において、y=0を代入して2次方程式を導出する。
- 2次方程式を解いて、グラフとx軸との共有点のx座標を求める
- グラフ・値域・共有点のx座標から定義域を求める。
- 求めた定義域が2次不等式の解
解法の手順は上述の通りです。ただし、2次不等式の左辺から作った2次方程式を、因数分解できたり、解の公式で解けたりすれば、2次不等式の解をすぐに求めることもできます。
2次不等式の解法・基本編では、2次方程式が異なる2つの実数解をもつ場合を取り上げました。
2次方程式が異なる2つの実数解をもつ場合、この実数解がグラフとx軸との共有点のx座標になります。ですから、2次方程式の実数解が分かれば、グラフと値域から定義域を求めることができます。
また、以下のように一般化もされています。
2次不等式の解
$2$ 次不等式
\begin{align*} \quad a{x}^{2}+bx+c \lt 0 \quad ( a \gt 0 \ , \ \alpha \lt \beta) \end{align*}について
\begin{align*} \quad a{x}^{2}+bx+c = 0 \end{align*}の解が
\begin{align*} \quad x=\alpha \ , \ \beta \end{align*}であるとき、$2$ 次不等式の解は
\begin{align*} \quad \alpha \lt x \lt \beta \end{align*}$2$ 次不等式
\begin{align*} \quad a{x}^{2}+bx+c \gt 0 \quad ( a \gt 0 \ , \ \alpha \lt \beta) \end{align*}について
\begin{align*} \quad a{x}^{2}+bx+c = 0 \end{align*}の解が
\begin{align*} \quad x=\alpha \ , \ \beta \end{align*}であるとき、$2$ 次不等式の解は
\begin{align*} \quad x \lt \alpha \ , \ \beta \lt x \end{align*}2次不等式の左辺を見て、左辺から作った2次方程式の解がすぐに分かりそうなら上述の解法を利用しましょう。当てはめるだけなので難しくありません。
実際は手順通りに考えているが、記述を省略して解いているだけ。
基本編に対して応用編では、左辺から作った2次方程式が実数解を1個(重解)または0個もつ場合です。グラフとx軸との共有点の個数で言えば、共有点が1個または0個の場合です。
(実数解が1個)=(共有点が1個),(実数解が0個)=(共有点が0個)
基本編と応用編との違いは、2次方程式の実数解をそのまま定義域に用いることができないことです。ですから、基本編の解法と区別する必要があります。
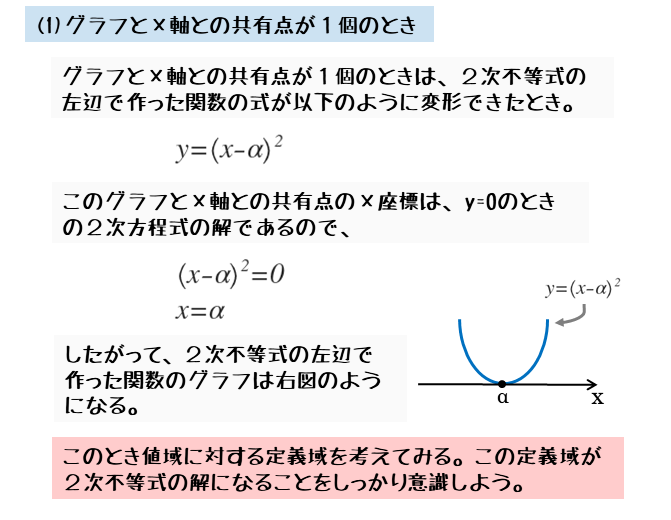
2次関数のグラフとx軸との共有点が1個の場合
グラフとx軸との共有点が1個の場合、2次関数においてy=0のときの2次方程式を考えてみましょう。
共有点が1個なので、2次方程式の実数解は1個だけ、すなわち重解になります。重解をもつとき、2次方程式はカッコの2乗の形に因数分解されます。
2次方程式が重解をもつ
$2$ 次方程式
\begin{align*} \quad a{x}^{2}+bx+c = 0 \end{align*}の解が
\begin{align*} \quad x=\alpha \end{align*}であるとき
\begin{align*} \quad a{\left( x – \alpha \right)}^{2} =0 \end{align*}と因数分解できる。
2次不等式の左辺がカッコの2乗の形に因数分解できるとき、グラフは共有点を1個もつようにx軸に接しています。このとき、共有点のx座標は2次方程式の重解です。
値域に対応する定義域を考える
さて、グラフとx軸との位置関係や共有点のx座標が分かったので、値域に対応する定義域を考えてみましょう。
2次不等式を2次関数と値域に置き換えたとき、値域は4つのパターンが考えられます。
4パターンの値域
- y>0のとき
- y≧0のとき
- y<0のとき
- y≦0のとき
それぞれの場合で定義域を考えます。
値域がy>0のとき
値域がy>0のとき、値域に対応するグラフは、y座標が0である共有点を除いた部分になります。
このグラフを参考にすると、値域に対応する定義域は、共有点のx座標α以外のすべての実数になります。ですから、2次不等式の解はx=α以外のすべての実数となります。
以下のように一般化されています。
2次不等式の解 1⃣
$2$ 次不等式
\begin{align*} \quad a{\left( x – \alpha \right)}^{2} \gt 0 \quad ( a \gt 0 ) \end{align*}の解は
\begin{align*} \quad x=\alpha \ \text{以外のすべての実数} \end{align*}共有点のx座標を定義域から除く必要があるので注意しよう。
値域がy≧0のとき
値域がy≧0のとき、値域に対応するグラフは、すべての部分が残ったグラフになります。
このグラフを参考にすると、値域に対応する定義域はすべての実数です。ですから、2次不等式の解はすべての実数となります。
以下のように一般化されています。
2次不等式の解 2⃣
$2$ 次不等式
\begin{align*} \quad a{\left( x – \alpha \right)}^{2} \geqq 0 \quad ( a \gt 0 ) \end{align*}の解は、すべての実数
値域がy<0のとき
値域がy<0のとき、値域に対応するグラフはありません。グラフが値域に含まれないからです。
グラフを参考にすると、値域に対応する定義域は存在しません。ですから、2次不等式の解は解なしとなります。
以下のように一般化されています。
2次不等式の解 3⃣
$2$ 次不等式
\begin{align*} \quad a{\left( x – \alpha \right)}^{2} \lt 0 \quad ( a \gt 0 ) \end{align*}の解は、解なし
値域がy≦0のとき
値域がy≦0のとき、値域に対応するグラフは共有点だけが残ります。グラフと言うよりも点と言った方が適切かもしれません。
グラフを参考にすると、値域に対応する定義域は共有点のx座標αだけです。ですから、2次不等式の解はx=αとなります。
以下のように一般化されています。
2次不等式の解 4⃣
$2$ 次不等式
\begin{align*} \quad a{\left( x – \alpha \right)}^{2} \leqq 0 \quad ( a \gt 0 ) \end{align*}の解は
\begin{align*} \quad x = \alpha \end{align*}このようにグラフとx軸との共有点が1個の場合、2次不等式の左辺を因数分解できたとしても、共有点のx座標がそのまま定義域に反映されるとは限りません。
ここが基本編のときと大きく異なるところで、ミスをしやすいところです。ですから、グラフを描いて定義域を考えることが大切です。
過程を省略するかどうかは別として、ミスを減らすには、グラフを描いて考えることが大切。
次は共有点が0個の場合を考えてみましょう。