2次関数|2次不等式の解法について(基本編)

今回は2次不等式の解法について学習しましょう。
2次不等式を解くためには、2次関数や2次方程式の知識が必要です。忘れてしまった人は復習しておきましょう。
こちらの記事で復習できます。
2次不等式について
2次不等式とは2次の項をもつ不等式のことです。たとえば、以下のような式が2次不等式です。
2次不等式の例
\begin{align*} &\quad {x}^{2}-3x+4 \leqq 0 \\[ 7pt ] &\quad {x}^{2}-3x-1 \geqq 0 \end{align*}このような2次不等式は、残念ながら1次不等式と同じように不等式の性質を利用して解けません。ですから別の手段で解きます。この別の手段が2次関数や2次方程式です。
2次不等式の解法は2次関数と2次方程式の合わせ技
2次不等式を解くとき、2次関数と2次方程式の知識を持ち合わせて解きます。
しかし、2次不等式は、不等式とあるように、2次関数や2次方程式などの等式とは異なります。
このままでは、2次関数と2次方程式を利用することができません。そのために、2次不等式に手を加えます。
2次不等式を関数化する
たとえば、以下のような2次不等式を解く場合を考えます。
例題
次の2次不等式の解を求めよ。
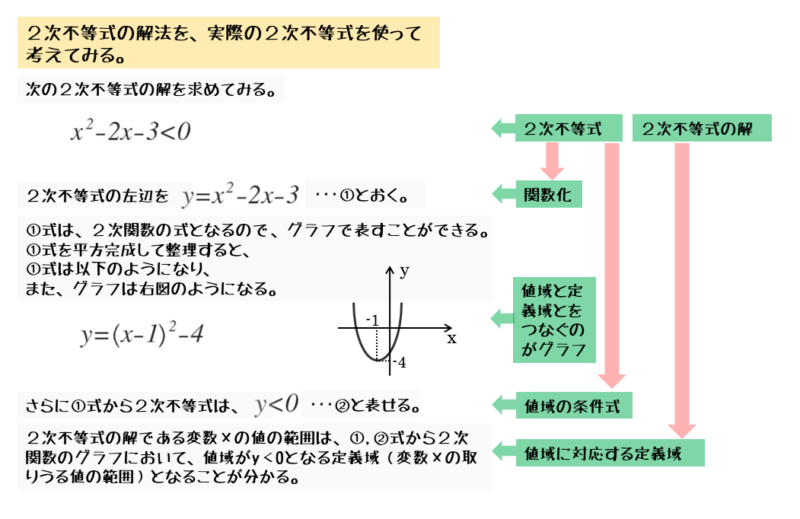
\begin{equation*} \quad {x}^{2}-2x-3 \lt 0 \end{equation*}この問題を2次関数や2次方程式を扱った問題に置き換えます。
例題の言い換え
次の $2$ 次関数の定義域を求めよ。
$2$ 次関数
\begin{equation*} \quad y = {x}^{2}-2x-3 \end{equation*}について、$y \lt 0$ を満たす
このように、2次不等式の問題は、2次関数の定義域や値域に関する問題に置き換えることができます。
置き換えから分かるように、2次不等式の解は、2次関数の値域を満たす定義域のことになります。
2次不等式の問題は、2次関数の定義域を求める問題にすり替えてしまおう。
(2次不等式)=(2次関数+値域)
2次不等式のままでは関数ではないので、左辺の2次式を「y=」でつないで2次関数の式にします。たったこれだけで2次不等式を関数にすることができます。
2次不等式から2次関数の式へ
\begin{align*} \quad {x}^{2}-2x-3 \lt 0 \end{align*}与えられた不等式において
\begin{align*} \quad y = {x}^{2}-2x-3 \end{align*}とおくと
\begin{align*} \quad y \lt 0 \end{align*}よって、与式は
\begin{align*} \quad y = {x}^{2}-2x-3 \quad \left( y \lt 0 \right) \end{align*}と置き換えできる。
2次関数ができれば、式の右辺を平方完成してグラフを描くことができるようになります。
ただし、与式は不等式だったので、グラフを描くときに値域の条件(y<0)を忘れないようにしましょう。
2次関数の値域を忘れずに
2次不等式から2次関数へ置き換えるとき、2次関数の値域の条件が出てきます。値域は、不等式の左辺をyとおいたときに得られる範囲です。
値域の条件を忘れずに
\begin{align*} \quad {x}^{2}-2x-3 \lt 0 \end{align*}与えられた不等式において
\begin{align*} \quad y = {x}^{2}-2x-3 \quad \cdots \text{①} \end{align*}とおくと
\begin{align*} \quad y \lt 0 \end{align*}これは①の値域である。
関数に値域が存在するとき、それに対応する定義域が存在します。
この定義域は、値域を満たすxの値の範囲です。そして、この定義域が2次不等式を満たすxの範囲、すなわち2次不等式の解になります。
これまでから分かるように、「2次不等式を解く」というのは「値域を満たす定義域を求める」ということを意味します。
定義域はグラフとx軸との共有点から求める
2次不等式から置き換えた2次関数で解く
\begin{align*} \quad {x}^{2}-2x-3 \lt 0 \end{align*}より
\begin{align*} \quad y = {x}^{2}-2x-3 \quad \left( y \lt 0 \right) \end{align*}例で言えば、値域y<0に対応する定義域が分かれば、2次不等式の解が分かります。
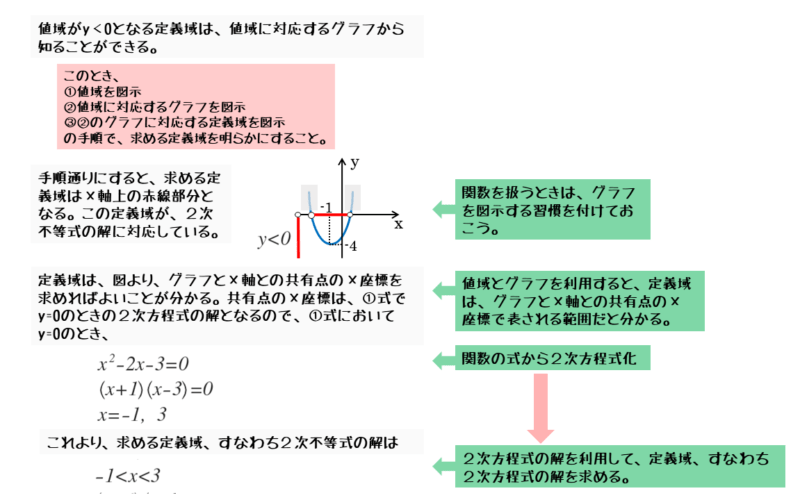
グラフを描くと、値域がy<0のとき、グラフはx軸よりも下の部分が残ります。
2次不等式を解くとき、2次関数に置き換えると、基本的にグラフがx軸の上か下のどちらが残るかを考えるだけで良くなる。値域がy<0のとき、グラフはx軸よりも下の部分が残る。
値域の不等号(<)からx軸(y=0のとき)との共有点が含まれないことは分かります。しかし、値域y<0に対応する定義域を求めるには、グラフとx軸との共有点のx座標を知る必要があります。
グラフとx軸との共有点のx座標は、2次関数の式においてy=0のときの2次方程式を解くことで得られます。
ここで2次方程式の登場です。グラフとx軸との共有点のx座標を求めるために2次方程式を利用します。
2次関数から2次方程式へ
\begin{align*} \quad {x}^{2}-2x-3 \lt 0 \end{align*}より
\begin{align*} \quad y = {x}^{2}-2x-3 \quad \left( y \lt 0 \right) \end{align*}ここで、$y=0$ のとき
\begin{align*} \quad {x}^{2}-2x-3 = 0 \end{align*}2次方程式を作ったら、それを解いて共有点のx座標を求めます。2次方程式を解くとき、因数分解または解の公式を利用します。求めた座標が定義域に必要な値です。
2次方程式を解く
\begin{align*} \quad \vdots \end{align*} \begin{align*} \quad {x}^{2}-2x-3 = 0 \end{align*}これを解くと
\begin{align*} \quad {x}^{2}-2x-3 &= 0 \\[ 7pt ] \left( x+1 \right)\left( x-3 \right) &= 0 \\[ 7pt ] \therefore \ x &= -1 \ , \ 3 \end{align*}共有点のx座標をグラフに追記し、グラフを見ながら値域に対応する定義域を調べます。この定義域が2次不等式の解となります。
値域に対応する定義域を求める
\begin{align*} \quad \vdots \end{align*} \begin{align*} \quad {x}^{2}-2x-3 &= 0 \\[ 7pt ] \left( x+1 \right)\left( x-3 \right) &= 0 \\[ 7pt ] \therefore \ x &= -1 \ , \ 3 \end{align*}よって、$y \lt0 $ を満たすのは
\begin{align*} \quad -1 \lt x \lt 3 \end{align*}これが $2$ 次不等式の解になる。
定義域を見ると、下限値や上限値が共有点のx座標になっていることに気付きます。このことは、グラフを描くとよく分かるでしょう。
関数の値域や定義域は、グラフを描いて求めよう。
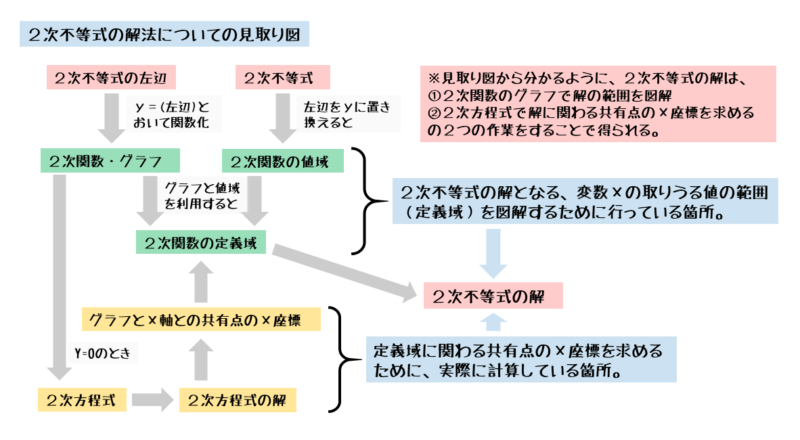
以上のようにして2次不等式を解きます。2次不等式を解く流れをまとめてみましょう。
2次不等式を解く流れ
- 2次不等式を、2次関数と値域に置き換える。
- 2次方程式を作り、グラフとx軸との共有点のx座標を求める。
- グラフ・値域・共有点のx座標を使って定義域(=2次不等式の解)を求める。
こうして2次不等式の解法を見てみると、「2次不等式を解く」と言うよりも「2次関数とその値域から定義域を求めている」と言った方がしっくりします。
2次不等式では、2次方程式と同じように2次関数のグラフに絡めた問題が多く出題されます。
ですから、方程式・不等式に限らず2次式を見たら2次関数のグラフをイメージすると、解決の糸口をつかめるかもしれません。
数学2になると、三角関数や指数・対数関数、そして3次関数などを学習する。これらも2次関数に帰結させて解くことが多い。今のうちに2次関数・2次方程式・2次不等式をしっかりとマスターしておきたい。
次は、2次不等式の解法をパターン別にみていきましょう。