積分法|定積分と区分求積法の関係について

よく出題される区間での面積
定積分と区分求積法の関係
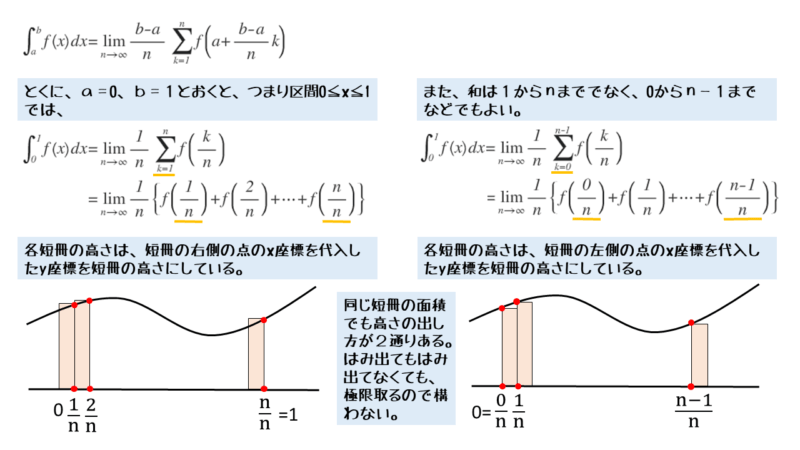
\begin{align*} \int_{a}^{b} {f \left( x \right) dx} =\lim_{n \to \infty}{\frac {b-a}{n}} \sum_{k=1}^{n}{f \left(a+\frac{b-a}{n} k \right)} \end{align*}上式について、特に出題される区間は、a=0,b=1(0≦x≦1)のときの区間です。このときの式は以下のようになります。
定積分と区分求積法の関係(区間0≦x≦1)
\begin{align*} \int_{0}^{1} {f \left(x \right) dx} =\lim_{n \to \infty}{\frac{1}{n}} \sum_{k=1}^{n}{f \left(\frac{k}{n} \right)} \end{align*}区間0≦x≦1をn等分すると、その区間には横幅の等しい長方形の短冊が横にn個並んだ状態になります。このとき、区間の長さは1なので、短冊の横幅はどれも等しくそれぞれ1/nです。
区間の長さは1で、短冊の横幅は1/n
また、縦の長さはグラフ上にある点のy座標を使います。このy座標を求めるには、グラフの式に点のx座標を代入します。
ここで、縦の長さについて注意点があります。図を見ると分かるように、短冊の作り方が2通りあることが分かります。
グラフ上にある点が、短冊の右上の頂点と一致する場合と、左上の頂点と一致する場合です。
どちらで短冊を作ったとしても、限りなく多くの短冊に分割するので結果は同じですが、和の取り方に違いが出るので注意が必要です。
和におけるkの値の違い
$0 \leqq x \leqq 1$ の区間で $n$ 等分したとき、短冊の頂点の選び方によって、和における $k$ の値の取り方が異なってくる。
左上の頂点を採用すれば、和における $k$ の値は「$k=0 \ , \cdots , \ n-1$」であり、右上の頂点を採用すれば、和における $k$ の値は「$k=1 \ , \cdots , \ n$」である。
各短冊の頂点の選び方で縦の長さが変わる
短冊の作り方に2通りありますが、そのとき、短冊の面積の和がどのように変わるのかを詳しく考えてみましょう。
短冊は、右上または左上の頂点がグラフ上にあるように作ります。
このとき、各短冊の横幅が1/nであることを利用すると、各頂点のx座標を求めることができます。
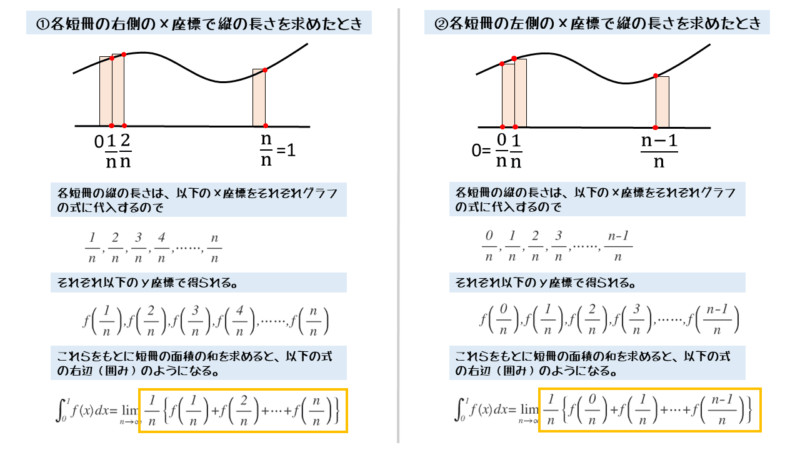
左から順に各頂点のx座標を並べてみると、頂点が右上のときと左上のときで異なることが分かります。
右上の頂点のときのx座標(区間0≦x≦1)
\begin{align*} \quad \frac{1}{n} \ , \ \frac{2}{n} \ , \ \frac{3}{n} \ , \ \cdots \ , \ \frac{n}{n} \end{align*}左上の頂点のときのx座標(区間0≦x≦1)
\begin{align*} \quad \frac{0}{n} \ , \ \frac{1}{n} \ ,\ \frac{2}{n} \ , \ \cdots \ , \ \frac{n-1}{n} \end{align*}これらのx座標をグラフの式に代入すると、頂点のy座標を得ることができます。このy座標が短冊の縦の長さになります。
左から順に各頂点のy座標を左から順に並べると以下のようになります。
右上の頂点のときのy座標(区間0≦x≦1)
\begin{align*} \quad f \left(\frac{1}{n} \right) \ , \ f \left(\frac{2}{n} \right) \ , \ f \left(\frac{3}{n} \right) \ , \ \cdots \ , \ f \left(\frac{n}{n} \right) \end{align*}左上の頂点のときのy座標(区間0≦x≦1)
\begin{align*} \quad f \left(\frac{0}{n} \right) \ , \ f \left(\frac{1}{n} \right) \ , \ f \left(\frac{2}{n} \right) \ , \ \cdots \ , \ f \left(\frac{n-1}{n} \right) \end{align*}これらから、それぞれの短冊の面積は以下のようになります。
右上の頂点で作ったときの各短冊の面積(区間0≦x≦1)
\begin{align*} \quad \frac{1}{n} \times f \left(\frac{1}{n} \right) \ , \ \frac{1}{n} \times f \left(\frac{2}{n} \right) \ , \ \frac{1}{n} \times f \left(\frac{3}{n} \right) \ , \ \cdots \ , \ \frac{1}{n} \times f \left(\frac {n}{n} \right) \end{align*}左上の頂点で作ったときの各短冊の面積(区間0≦x≦1)
\begin{align*} \quad \frac{1}{n} \times f \left(\frac{0}{n} \right) \ , \ \frac{1}{n} \times f \left(\frac{1}{n} \right) \ , \ \frac{1}{n} \times f \left(\frac{2}{n} \right) \ , \ \cdots \ , \ \frac{1}{n} \times f \left(\frac{n-1}{n} \right) \end{align*}さいごに各短冊の面積の和を取り、共通因数の1/nでくくると以下のようになります。
右上の頂点で作ったときの面積の和(区間0≦x≦1)
\begin{align*} \quad &\frac{1}{n} \times \left\{f \left(\frac{1}{n} \right) + f \left(\frac{2}{n} \right) + f \left(\frac{3}{n} \right) + \ \cdots \ f \left(\frac{n}{n} \right) \right\} \\[ 7pt ] = \ &\frac{1}{n} \left\{f \left(\frac{1}{n} \right) + f \left(\frac{2}{n} \right) + f \left(\frac{3}{n} \right) + \ \cdots \ f \left(\frac{n}{n} \right) \right\} \end{align*}左上の頂点で作ったときの面積の和(区間0≦x≦1)
\begin{align*} \quad &\frac{1}{n} \times \left\{ f \left(\frac{0}{n} \right) + f \left(\frac{1}{n} \right) + f \left(\frac{2}{n} \right) + \ \cdots \ f \left(\frac{n-1}{n} \right) \right\} \\[ 7pt ] = \ &\frac{1}{n} \left\{ f \left(\frac{0}{n} \right) + f \left(\frac{1}{n} \right) + f \left(\frac{2}{n} \right) + \ \cdots \ f \left(\frac{n-1}{n} \right) \right\} \end{align*}規則的に変化する数の和はΣを使う
短冊の面積の和を何度も記述するのは面倒です。各項が規則的に変化するので、和を表すΣ(シグマ)を用いると簡潔になります。
x座標の分子に注目すると、0からn-1、あるいは1 からnの整数が順に並ぶように規則的に変化しています。
右上の頂点で作ったときの面積の和(区間0≦x≦1)
\begin{align*} \quad \frac{1}{n} \cdot f \left(\frac{1}{n} \right) \ + \ \frac{1}{n} \cdot f \left(\frac{2}{n} \right) \ + \ \frac{1}{n} \cdot f \left(\frac{3}{n} \right) \ + \ \cdots \ + \ \frac{1}{n} \cdot f \left(\frac{n}{n} \right) \end{align*}左上の頂点で作ったときの面積の和(区間0≦x≦1)
\begin{align*} \quad \frac{1}{n} \cdot f \left(\frac{0}{n} \right) \ + \ \frac{1}{n} \cdot f \left(\frac{1}{n} \right) \ + \ \frac{1}{n} \cdot f \left(\frac{2}{n} \right) \ + \ \cdots \ + \ \frac{1}{n} \cdot f \left(\frac{n-1}{n} \right) \end{align*}この規則性が分かれば、k番目の短冊の面積は以下のように表されます。
k番目の短冊の面積
\begin{align*} \quad \frac{1}{n} \cdot f \left(\frac{k}{n} \right) \end{align*}あとは変数kがどの範囲で変わるのかに注意すれば、面積の和をΣで表すことができます。Σ記号は便利なので使えるようにしておきましょう。
右上の頂点で作ったときの面積の和(区間0≦x≦1)
\begin{align*} &\frac{1}{n} \cdot f \left(\frac{1}{n} \right) \ + \ \frac{1}{n} \cdot f \left(\frac{2}{n} \right) \ + \ \frac{1}{n} \cdot f \left(\frac{3}{n} \right) \ + \ \cdots \ + \ \frac{1}{n} \cdot f \left(\frac{n}{n} \right) \\[ 7pt ] = \ &\sum_{k=1}^{n}{\frac{1}{n} \cdot f \left(\frac{k}{n} \right)} \\[ 7pt ] = \ &\frac{1}{n} \sum_{k=1}^{n}{f \left(\frac{k}{n} \right)} \end{align*}左上の頂点で作ったときの面積の和(区間0≦x≦1)
\begin{align*} &\frac{1}{n} \cdot f \left(\frac{0}{n} \right) \ + \ \frac{1}{n} \cdot f \left(\frac{1}{n} \right) \ + \ \frac{1}{n} \cdot f \left(\frac{2}{n} \right) \ + \ \cdots \ + \ \frac{1}{n} \cdot f \left(\frac{n-1}{n} \right) \\[ 7pt ] = \ &\sum_{k=0}^{n-1}{\frac{1}{n} \cdot f \left(\frac{k}{n} \right)} \\[ 7pt ] = \ &\frac{1}{n} \sum_{k=0}^{n-1}{f \left(\frac{k}{n} \right)} \end{align*}変数kの値が変化する範囲が、頂点の選び方(右上または左上)によって変わる。
次は、区分求積法を扱った問題を解いてみましょう。