集合と論理|集合と要素について

今回から「集合と論理」という単元を学習します。
「数と式」では基本的に数や式の扱い方を学習しますが、「集合と論理」では数学的な思考の仕方を学習します。計算力よりも論理的な思考力を養うことに力点が置かれているので、すぐに理解できなくてもじっくりと考えることが大切です。
最初は用語やルールの解説なので、しっかり把握しましょう。何事も最初が肝心です。
記事の画像が見辛いときはクリックすると拡大できます。
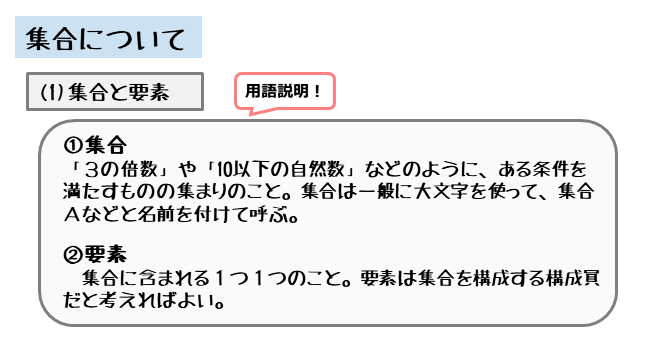
集合と要素
集合とは、ある条件を満たすものの集まりのことです。名前の「集まる、合わさる」という言葉から、何かが集まっているイメージが頭に浮かべば良いでしょう。
要素とは、集合の中にある1つ1つのもののことです。ある条件を満たすものが要素で、その要素が集まって集合を作っています。
また、集合や要素を表すために、アルファベットが使われます。たとえば、集合であれば大文字を使って集合A、要素であれば小文字を使って要素aなどと表されます。
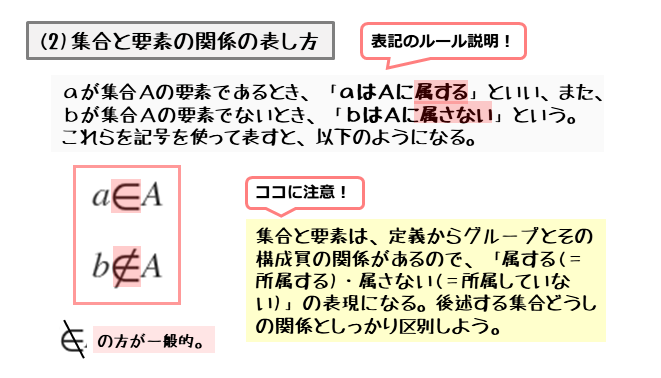
集合と要素の関係を表す
集合と要素の関係は、グループ(主)とそれに所属している構成員(従)との関係に似ています。ですから「属する(=所属している)」や「属さない(=所属していない)」といった表現をします。
たとえば、集合Aに要素aが属しているとき、「aはAに属する」と言います。また、集合Aに要素bが属していないとき、「bはAに属さない」と言います。
「属する」や「属さない」を表す記号があるので、この記号を使って集合と要素との主従関係を表すことができます。
集合と要素の関係の表し方
( $a$ は $A$ に属する)⇔ $a \in A$
( $b$ は $A$ に属さない)⇔ $b \notin A$
まとめると以下のようになります。
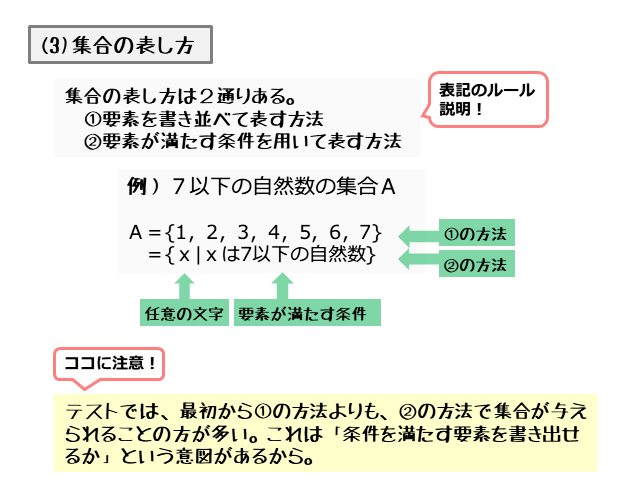
集合の表し方
集合はある条件を満たす要素の集まりです。ですから、条件によっては、たくさんの要素が集合に属している可能性があります。
このような集合を表すには、次の2通りの方法があります。
集合の表し方
- 条件を満たす要素を書き並べる方法
- 要素が満たす条件を述べる方法
要素を書き並べる方法では、書き並べた要素全体を波カッコ({ )でくくり、1つのかたまり(=集合)にしてしまいます。
条件を述べる方法は、要素を書き並べることが難しいときに用いられることが多いです。この方法では、要素が満たす条件を任意の文字(xやaなど)を用いた数式や説明で表します。
例えば、集合Aが5以下の自然数の集合であるとします。この集合Aをそれぞれの方法で表してみましょう。
集合の表し方は2通り
集合 $A$ が $5$ 以下の自然数の集合であるとき
要素を書き並べて表すと
\begin{align*} \quad A = \left\{1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 5 \right\} \end{align*}要素が満たす条件で表すと
\begin{align*} \quad A = \left\{x \ | \ x \ \text{は $5$ 以下の自然数} \right\} \end{align*}問題では「要素が満たす条件を述べる方法」で表されることが多い。これは「条件を満たす要素を書き出せるか」という意図があるから。条件を満たす要素を自分で書き出せるようにしておこう。
まとめると以下のようになります。
集合の種類
集合は、その性質や集合どうしの関係によって、3種類に分類されます。この分類を知っておくと、集合を扱いやすくなります。
部分集合
部分集合とは、名前の通り、ある集合の一部となっている集合のことです。
たとえば、2つの集合A,Bについて、集合Bの要素がすべて集合Aに属しているとき、集合Bは集合Aの一部になっています。このようなとき「BはAの部分集合である」と言います。
また、「集合Aと集合Bは包含関係にある」や「集合Bは集合Aに含まれる」などと言う場合もあります。どれも同じ内容の表現なので混乱しないようにしましょう。
部分集合に関係する表現
集合 $B$ が集合 $A$ の部分集合である
= 集合 $B$ の要素がすべて集合 $A$ に属している
= 集合 $A$ と集合 $B$ は包含関係にある
= 集合 $B$ は集合 $A$ に含まれる
空集合
空集合とは、空っぽの集合のことで、条件を満たす要素がない集合のことです。空集合は要素をもたないので、∅と表します。
空集合は要素を持たない空っぽの集合なので、どの集合にも含まれることが可能です。ですから、空集合はすべての集合の部分集合になります。
空集合の表し方
集合 $A$ が空集合であるとき
\begin{align*} \quad A = \varnothing \end{align*}全体集合
全体集合は、集合や要素を考えるときに予め決められた集合のことで、よくアルファベットのUが割り当てられます。
たとえば、自然数を考えるとき、5以下の自然数が属している集合をAとします。
集合Aの要素は、5以下の自然数になるので有限です。それに対して、集合Aに属さない要素は、5以下の自然数以外になるので無限にあります。
これを防ぐために全体集合Uを使います。たとえば、全体集合Uが10以下の自然数の集合だとすれば、集合Aに属さない要素も有限個になります。
このように全体集合が大きな囲いのようになります。
全体集合のおかげで、最初から扱う要素の総数が決まり、しかも集合外の要素も有限個になった状態で集合や要素を考えることができます。ですから、全体集合があれば、全体集合に属さない要素を考える必要がなくなります。
集合の種類をまとめると以下のようになります。
集合どうしの関係の表し方
2つの集合A,Bが包含関係にあるとき、記号や図を使って表すことができます。記号は「⊂」や「⊃」を使いますが、集合と要素の関係を表す記号に似ているので、しっかり区別しましょう。
集合の包含関係を表す記号
集合 $B$ が集合 $A$ に含まれるとき
\begin{align*} \quad B \subset A \ \text{または} \ A \supset B \end{align*}また、集合の関係を表す図のことをベン図と言います。
たとえば、集合Aが集合Bを含む包含関係にあるとき、集合Aが集合Bをすっぽりと包むように描きます。
余談ですが、2016年のセンター試験で「 $\in$,$\notin$,$\subset$,$\supset$ 」などの記号を使い分ける問題が出題されています。
「センター試験にこんなに易しい問題を出題して良いの? 受験生を舐め過ぎじゃないの?」と驚いた記憶があります。あまりにも基本的過ぎて、入試レベルではほとんど見かけない問題です。間違えた人が意外といたかもしれません。
集合や要素を扱うときは可視化しよう
集合や要素を扱うとき、とにかく可視化することが大切です。複数の集合を扱うことが多くなるので、可視化することはとても有効です。
集合と要素であれば、要素を書き並べて表すと良いでしょう。また、集合どうしであれば、ベン図を利用しましょう。
特に、ベン図を使うと包含関係や属す要素などが一目で把握できます。
作図したり、表にまとめたりすることによって、条件やヒントの整理に役立ちます。方針を立てやすくなるので、図や表を積極的に利用しましょう。
これらを基本作業として習慣化しておくと、問題を解く前に材料が揃った状態になり、スムーズに解答していくことができるでしょう。
次は、集合や要素を扱った問題を実際に解いてみましょう。用語や記号の定義を意識しながら解きましょう。