図形と計量|正弦定理・余弦定理、面積への応用について

今回は、正弦定理や余弦定理の図形への応用を学習しましょう。三角比を扱った総合問題です。
総合問題になると、三角形はもちろん、四角形や円とも絡めた問題も出題されます。図形の定義や性質だけでなく、それらに三角比がどのように関係してくるかを把握する必要があります。
今まで学習してきた知識を優先順位を考えながら使い分け、要求される数量を求めなければなりません。まずは解までの一連の流れを把握し、次にポイントを細かくチェックしていきましょう。
記事の画像が見辛いときはクリックすると拡大できます。
三角比を扱った総合問題
三角比を扱った総合問題では、特に円や四角形と絡めた問題が多く出題されます。たとえば、正弦定理は、外接円と関係が深い定理です。
他には、三角形の内接円や、円に内接する四角形を扱った問題も出題されます。図形ごとにどの知識と関係が深いのかをきちんと整理しましょう。
内接円の半径と三角形の面積
先ほど外接円の話が出ましたが、三角形の内接円も扱います。たとえば、内接円の半径を求める問題が出題されます。
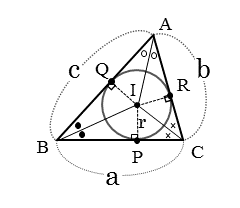
三角形の内接円とは、三角形の3辺に内側から接する円のことです。3辺が内接円の接線になっています。
また、内接円の中心のことを内心と言います。内心は、三角形の3つの内角の二等分線の交点となります。
そして、内心と接点とを結んだ線分は、内接円の半径です。この内接円の半径を使って、三角形の面積を表すことができます。
図の△ABCを使って考えてみましょう。
三角形の頂点A,B,Cと内心Iとをそれぞれ結ぶと、△ABCは3つの三角形△IBC,△IAC,△IABに分解されます。
分解後の3つの三角形の面積の和は、もとの三角形の面積に等しくなります。
三角形と内接円の関係 1⃣
\begin{align*} \quad \triangle ABC = \triangle IBC + \triangle IAC +\triangle IAB \end{align*}このとき、3つの三角形△IBC,△IAC,△IABの底辺は、△ABCの辺になります。また、3つの三角形の高さは、ともに内接円の半径となります。
このような関係をもとに、△ABCの面積を求めてみましょう。3つの三角形の面積の和を取ります。
三角形と内接円の関係 2⃣
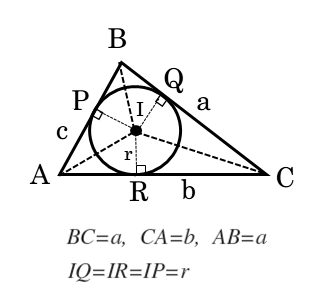
$BC=a \ , \ CA=b \ , \ AB=c \ , \ IQ=IR=IP=r$ とする。
\begin{align*} \triangle ABC &= \triangle IBC + \triangle IAC +\triangle IAB \\[ 7pt ] &= \frac{1}{2} \cdot BC \cdot IQ + \frac{1}{2} \cdot CA \cdot IR +\frac{1}{2} \cdot AB \cdot IP \\[ 7pt ] &= \frac{1}{2}ar + \frac{1}{2}br +\frac{1}{2}cr \\[ 7pt ] &= \frac{1}{2} r \left( a+b+c \right) \end{align*}したがって
\begin{align*} \quad \triangle ABC = \frac{1}{2} r \left( a+b+c \right) \end{align*}導出された式から分かるように、三角形の面積は、三角形の3辺と内接円の半径とを用いて表されます。この関係を利用すると、三角形の面積から内接円の半径を求めることができます。
三角形と内接円の話が出てきたら、まずこの関係式を利用する問題。頻出なのは内接円の半径を求める問題。
三角形と円に内接する四角形
四角形は三角形2つぶん
三角比を扱った総合問題では、四角形も扱います。ただし、三角比は基本的に三角形で成り立つものなので、四角形のままでは具合が悪いです。
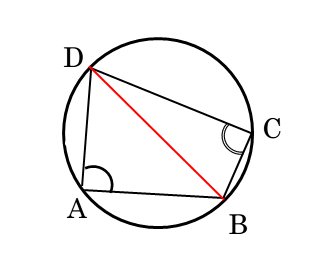
四角形のままで処理せずに、三角形に分けます。そのために、対角線を利用します。
対角線によって、四角形が2つの三角形に分割されます。
三角形に分割できれば、三角比を利用することが可能になります。
対角線の引き方は2通りあるが、問題に合わせて分割しよう。
円に内接する四角形の対角
また、円に内接する四角形も出題されます。
四角形が円に内接するとき、四角形の頂点はすべて円周上にあります。円の方から見れば、円は四角形に外接しているので四角形の外接円と言えます。
このような四角形と円では、四角形の対角の関係を知っておく必要があります。円周角と中心角の性質を利用して導出されます。
円に内接する四角形の対角
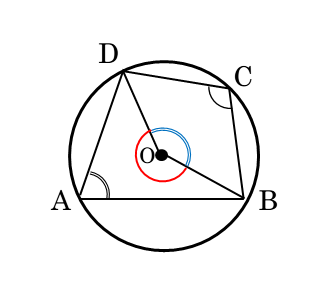
$\stackrel{ \Large \frown }{ BCD }$ に対する中心角を $\angle BO_{1}D$ 、$\stackrel{ \Large \frown }{ BAD }$ に対する中心角を $\angle BO_{2}D$ とする。
円周角と中心角の性質から
\begin{align*} &\quad \angle BO_{1}D = 2 \angle BAD \\[ 7pt ] &\quad \angle BO_{2}D = 2 \angle BCD \end{align*}ここで
\begin{align*} \quad \angle BO_{1}D + \angle BO_{2}D = 360^{\circ} \end{align*}であるので
\begin{align*} \quad 2 \angle BAD + 2 \angle BCD = 360^{\circ} \end{align*}したがって
\begin{align*} \quad \angle BAD + \angle BCD = 180^{\circ} \end{align*}導出された式から分かるように、円に内接する四角形の対角の和は180°になります。これを利用すると、一方の内角の大きさから、他方の内角の大きさを求めることができます。
この対角の和を上手に利用するには、三角比の相互関係を使いこなせないといけません。
対角の和と関係の深い三角比の相互関係
\begin{align*} &\quad \sin \left(180^{\circ} – \theta \right) = \sin \theta \\[ 10pt ] &\quad \cos \left(180^{\circ} – \theta \right) = -\cos \theta \\[ 10pt ] &\quad \tan \left(180^{\circ} – \theta \right) = -\tan \theta \end{align*}円に内接する四角形の扱い方を整理しましょう。
円に内接する四角形の扱い方
- 四角形を対角線で2つの三角形に分解する
- 各三角形について、正弦定理や余弦定理を利用する
- 円に内接する四角形の対角の和も利用する
円に内接する四角形では、「対角線で三角形に分割」「対角の和」を利用しよう。
次は、内接円を扱った問題を実際に解いてみましょう。
内接円を扱った問題を解いてみよう
次の問題を考えてみましょう。内接円を扱った基本的な問題ですが、頻出の問題です。
問1(3)を解くために(1),(2)があります。問題全体の流れを意識しつつ、計算ミスをせずに解きましょう。
問1(1)の解答・解説
問1(1)
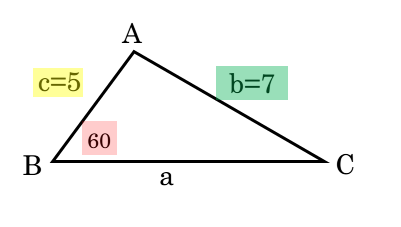
$\triangle ABC$ において、$B=60^{\circ} \ , \ b=7 \ , \ c=5$ のとき、次の値を求めよ。
\begin{align*} \quad a \end{align*}問1(1)は、辺BCの長さaを求める問題です。∠Bの大きさと2辺の長さが与えられています。辺や角の大小関係に注意して作図しましょう。
与えられた条件から、余弦定理を利用することができます。ここで注意したいのは、3つの余弦定理の式のうちどれを使うかです。余弦定理の式は3つあります。
余弦定理
\begin{align*} &\quad a^{2} = b^{2} + c^{2} -2bc\cos A \\[ 7pt ] &\quad b^{2} = a^{2} + c^{2} -2ac\cos B \\[ 7pt ] &\quad c^{2} = a^{2} + b^{2} -2ab\cos C \end{align*}1番目の式であれば、aの値を求めることができそうですが、∠Aの大きさが分かっていないので使えません。ですから、どの余弦定理の式を使うかは、角の大きさが分かっているかどうかで判断します。
∠Bの大きさが分かっているので、以下の式を使います。
問1(1)で使う余弦定理の式
\begin{align*} \quad b^{2} = a^{2} + c^{2} -2ac\cos B \end{align*}これなら、∠Bの大きさが分かっているので、a以外はすべて数になり、aについての方程式を導くことができます。
問1(1)の解答例
$\triangle ABC$ において、余弦定理より
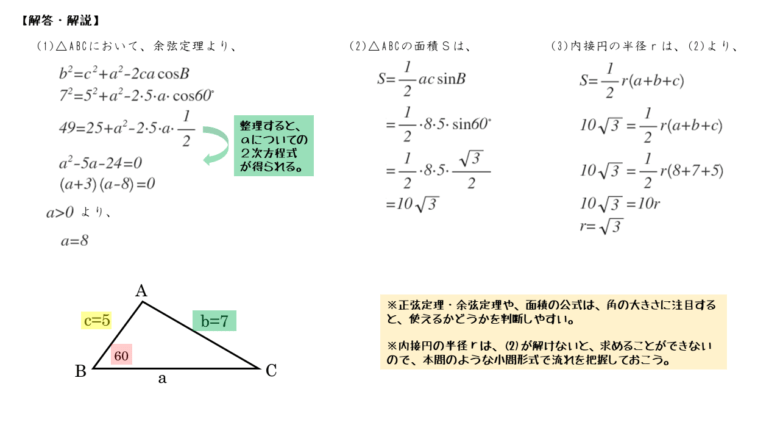
\begin{align*} &\quad b^{2} = a^{2} + c^{2} -2ac\cos B \\[ 7pt ] &\quad 7^{2} = a^{2} + 5^{2} -2 \cdot a \cdot 5 \cdot \cos 60^{\circ} \\[ 7pt ] &\quad 49 = a^{2} + 25 -2 \cdot a \cdot 5 \cdot \frac{1}{2} \\[ 7pt ] &\quad 49 = a^{2} + 25 -5a \\[ 7pt ] &\quad a^{2} -5a -24 = 0 \\[ 7pt ] &\quad \left(a+3 \right) \left(a-8 \right) = 0 \end{align*}$a \gt 0$ より
\begin{align*} \quad a = 8 \end{align*}余弦定理の式に代入すると、aについての2次方程式が得られました。少し応用的な使い方になりますが、角の大きさが分かっている式を使えば、きちんと方程式を導出することができます。
2次方程式なので解が2つ出てきますが、辺の長さを求めたいので先に吟味して解を求めましょう。
問1(2)の解答・解説
問1(2)
$\triangle ABC$ において、$B=60^{\circ} \ , \ b=7 \ , \ c=5$ のとき、次の値を求めよ。
\begin{align*} \quad \triangle ABC \ \text{の面積} \ S \end{align*}問1(2)は、△ABCの面積を求める問題です。面積の公式を利用したいところです。
三角形の面積の公式
三角形の2辺の長さを $x \ , \ y$、その挟む角の大きさを $\theta$ とする。
このとき、三角形の面積 $S$ は
\begin{align*} \quad S = \frac{1}{2} xy \sin \theta \end{align*}公式を利用するには、2辺の長さとその挟む角の大きさが分かっていることが条件です。
すでに∠Bの大きさが分かっており、∠Bを挟む2辺はAB,BCですが、どちらも長さが分かっているので公式を利用できます。
問1(2)の解答例
$(1)$ より
\begin{align*} \quad a= 8 \end{align*}よって
\begin{align*} \quad S &= \frac{1}{2} ac \sin B \\[ 7pt ] &= \frac{1}{2} \cdot 8 \cdot 5 \cdot \sin 60^{\circ} \\[ 7pt ] &= \frac{1}{2} \cdot 8 \cdot 5 \cdot \frac{\sqrt{3}}{2} \\[ 7pt ] &= 10 \sqrt{3} \end{align*}求める面積 $S$ は
\begin{align*} \quad S= 10 \sqrt{3} \end{align*}問1(2)を解くとき、(1)の結果を利用するので計算ミスに気を付けよう。計算ミスは、小問形式では致命的なミスになります。
問1(3)の解答・解説
問1(3)
$\triangle ABC$ において、$B=60^{\circ} \ , \ b=7 \ , \ c=5$ のとき、次の値を求めよ。
\begin{align*} \quad \triangle ABC \ \text{の内接円の半径} \ r \end{align*}問1(3)は、三角形の内接円の半径を求める問題です。内接円の半径は、三角形の面積を利用して求めます。そのためにも(2)を確実に解いておく必要があります。
問1(3)の解答例
$(1) \ , \ (2)$ より
\begin{align*} &\quad a= 8 \\[ 7pt ] &\quad S= 10 \sqrt{3} \end{align*}よって
\begin{align*} \quad S &= \frac{1}{2} r \left( a+b+c \right) \\[ 7pt ] 10 \sqrt{3} &= \frac{1}{2} \cdot r \cdot \left( 8+7+5 \right) \\[ 7pt ] 10 \sqrt{3} &= \frac{1}{2} \cdot r \cdot 20 \\[ 5pt ] 10 \sqrt{3} &= 10r \\[ 7pt ] r &= \sqrt{3} \end{align*}求める内接円の半径 $r$ は
\begin{align*} \quad r= \sqrt{3} \end{align*}値を代入する前に、内接円の半径rについて変形しても構いません。代入する値が分数などでなければ、こちらの方が楽な計算になることが多いです。状況に応じて使い分けましょう。
問1(3)の別解例
$(1) \ , \ (2)$ より
\begin{align*} &\quad a= 8 \\[ 7pt ] &\quad S= 10 \sqrt{3} \end{align*}また
\begin{align*} \quad S = \frac{1}{2} r \left( a+b+c \right) \end{align*}これを $r$ について整理すると
\begin{align*} \quad r = \frac{2S}{a+b+c} \end{align*}より
\begin{align*} \quad r &= \frac{2 \cdot 10 \sqrt{3}}{8+7+5} \\[ 7pt ] &= \frac{2 \cdot 10 \sqrt{3}}{20} \\[ 7pt ] &= \sqrt{3} \end{align*}求める内接円の半径 $r$ は
\begin{align*} \quad r= \sqrt{3} \end{align*}内接円の半径を用いた三角形の面積の式に、対応する値を代入します。すると、内接円の半径rについての方程式を導出できます。
また、別解であれば、右辺だけの計算になるので、気分的に楽かもしれません。
問1のポイントと解答例をまとめると以下のようになります。計算のやり方が若干異なるかもしれませんが、方針に変わりはありません。自分なりに負担が少なくミスをしにくい計算のやり方を研究して下さい。
入試レベルになると、(1)や(2)が省略されていたり、最初から(3)だけの問題になっていたりする。省略されても大丈夫なように、問1全体の流れをしっかり把握しておこう。
次は、四角形を扱った問題を解いてみましょう。