図形と計量｜正弦定理と余弦定理を扱った問題を解いてみよう
今回は、正弦定理や余弦定理を扱った問題を実際に解いてみましょう。
定理や公式は覚えるだけでなく、その使い方をマスターしなければ問題を解くことはできません。定理や公式は使ってこそです。
どんな条件のときに定理や公式を利用できるのか、しっかり把握することが大切です。覚えたくらいで満足しないようにしましょう。
記事の画像が見辛いときはクリックすると拡大できます。
正弦定理や余弦定理を扱った問題を解いてみよう
基礎レベルの問題であれば、「正弦定理」などとタイトルが付いてることがあります。それが原因で、ネタが割れた状態で解くことになります。
基礎レベルの問題では、学習したことの使い方や問題のパターンを知ることが目的なので、使うネタが分かっているのは当然です。
ただ、問題のレベルが上がってくると、その辺りが巧妙に隠されています。そうなると、何を使えば良いか分かり辛くなってきます。
しかし、演習を重ねていくと、頭の中が整理されてきます。そこまで習熟度が上がると、問題文を読んだとき「あのパターンだな」と分かるようになります。
自分なりに問題をパターン化しておき、そのような問題では悩まずに秒殺しつつ、思考力や応用力を問われるような問題（楽しみたい問題）に時間を使えるようにしましょう。
正弦定理の使い方
問題を解く前に正弦定理の式を思い出してみましょう。
正弦定理
$\triangle ABC$ の外接円の半径を $R$ とすると
\begin{align*} \quad \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R \end{align*}正弦定理の式は、一般に、４つの数量が等しいことを１つの等式にまとめて表します。ただし、実際に利用するとなると、２つの数量を選んで方程式を作ります。このとき、方程式の作り方には２パターンあります。
１つ目のパターンは、外接円の半径、角の大きさ、辺の長さの３つのうちどれかを求める使い方です。
角と辺は、対角と対辺の関係にあります。最も多く使われるのは、外接円の半径を求めるときです。
正弦定理の使い方パターン１
\begin{align*} &\quad \frac{a}{\sin A} = 2R \\[ 7pt ] &\quad \frac{b}{\sin B} = 2R \\[ 7pt ] &\quad \frac{c}{\sin C} = 2R \end{align*}２つ目のパターンは、対角と対辺の関係にある２組から、角の大きさ、または辺の長さを求める使い方です。角が２つと辺が２つ使われた式なので、３つの数量が予め分かっていなければなりません。
正弦定理の使い方パターン２
\begin{align*} &\quad \frac{a}{\sin A} = \frac{b}{\sin B} \\[ 7pt ] &\quad \frac{b}{\sin B} = \frac{c}{\sin C} \\[ 7pt ] &\quad \frac{c}{\sin C} = \frac{a}{\sin A} \end{align*}どちらの使い方であっても、対角と対辺の関係に注目することが大切です。
正弦定理の使い方を整理できたところで、次の問題を解いてみましょう。
正弦定理を扱った問題を解いてみよう
問１(1)の解答・解説
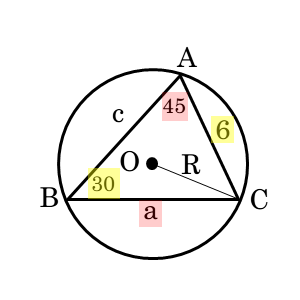
問１(1)
$\triangle ABC$ において、次の値を求めよ。
\begin{align*} \quad b=6 \ , \ A=45^{\circ} \ , \ B=30^{\circ} \end{align*}のとき $a$
問題をよく観察しつつ、作図してみましょう。図形の問題なので、作図すると角や辺の関係を把握しやすくなります。ただし、辺や角の大小関係に気を付けましょう。
与えられた条件をもとに作図します。
ｂ，Ｂは対角と対辺の関係にある辺と角です。また、Ａは、 求めたいａの対角です。
与えられた条件から、正弦定理のパターン２を利用します。
公式を早く覚えるためにも、１行目にそのまま公式を書きます。求めたいａについて等式を変形してから、与えられた値を代入します。
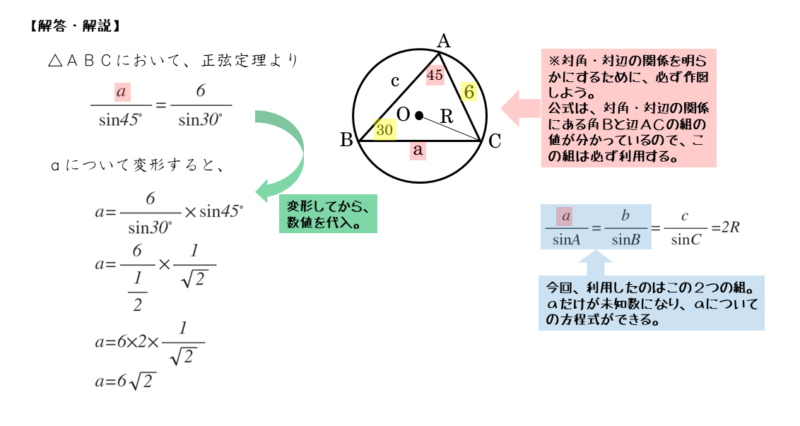
問１(1)の解答例
正弦定理より
\begin{align*} \quad \frac{a}{\sin A} = \frac{b}{\sin B} \end{align*}より
\begin{align*} \quad a=\frac{b \sin A}{\sin B} \end{align*}$b=6 \ , \ A=45^{\circ} \ , \ B=30^{\circ}$ より
\begin{align*} \quad a &=\frac{6 \sin 45^{\circ}}{\sin 30^{\circ}} \\[ 7pt ] &= \frac{6 \cdot \frac{1}{\sqrt{2}}}{\frac{1}{2}} \\[ 7pt ] &= \frac{6 \cdot 2}{\sqrt{2}} \\[ 7pt ] &= 6 \sqrt{2} \end{align*}値を代入するのは、ａについて変形する前でも構いません。とにかく計算ミスの少ないやり方を自分なりに見つけましょう。
問１(1)のポイントと解答例をまとめると以下のようになります。
学習したての頃は公式がうろ覚えであることが多い。できるだけ早く覚えるには、公式を使いながら覚えるのがコツ。
具体的には、問題を解くときに
- 公式を書く
- その文字に対応する数を代入する
の順に解いていくと良い。この手順で問題を解いていくと、割と短時間で公式を覚えることができる。
また、文字と数の対応関係も分かり、公式の使い方を要領よくマスターできるのも利点。
分数の中に分数がある計算
正弦定理を使った計算では、三角比が分数なので、分数の中に分数がある計算が出てきます。
仕組みを知っておくと、ちょっとしたコツで簡単に変形できるようになります。例を挙げて計算の仕組みを考えてみましょう。
分母に分数があるときを考えます。分母の分数は割る数になるので、分数を割り算に置き換えることができます。分数の割り算では、割る数の逆数をとって掛け算します。
分母に分数があるとき
\begin{align*} \quad \frac{3}{\frac{2}{5}} &= 3 \div \frac{2}{5} \\[ 10pt ] &= 3 \times \frac{5}{2} \\[ 10pt ] &= \frac{3 \times 5}{2} \\[ 10pt ] \therefore \ \frac{3}{\frac{2}{5}} &= \frac{3 \times 5}{2} \end{align*}計算過程から分かるように、分母に分数があるとき、分母の分数の逆数を取ります。その結果、分母の分数がひっくり返ったような分数になっています。
このことを知っていれば、わざわざ割り算に戻したり、逆数を取ったりする手間を掛けずに済みます。
分母にある分数はひっくり返せ。割り算に戻したり、分母と分子に数を掛けたりする必要なし。
問１(2)の解答・解説
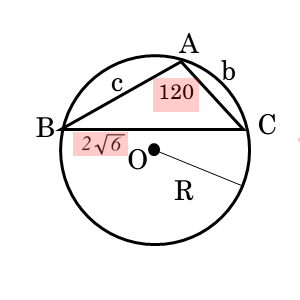
問１(2)
$\triangle ABC$ において、次の値を求めよ。
\begin{align*} \quad a=2\sqrt{6} \ , \ A=120^{\circ} \end{align*}のとき、外接円の半径 $R$
問１(2)では、外接円の半径という文言があるので、正弦定理のパターン１を利用する問題です。対角と対辺の関係にある角と辺が与えられています。
与えられた条件をもとに作図します。
ａ，Ａは対角と対辺の関係にある辺と角です。求めたいのは、△ＡＢＣの外接円の半径Ｒです。
与えられた条件から、正弦定理のパターン１を利用します。
１行目にそのまま公式を書きます。求めたいＲについて等式を変形してから、与えられた値を代入します。
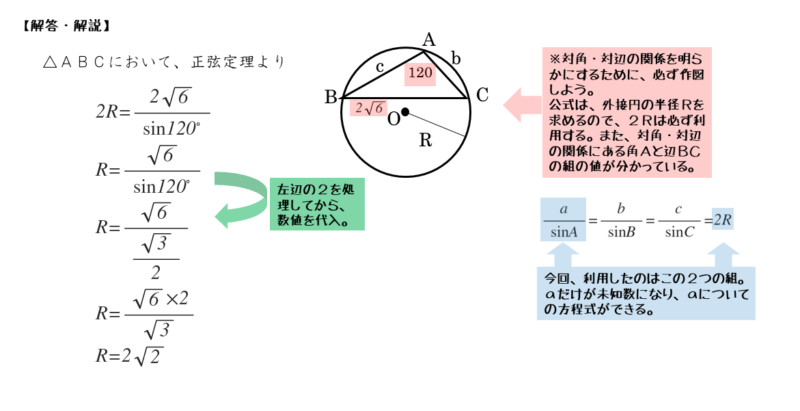
問１(2)の解答例
正弦定理より
\begin{align*} \quad 2R = \frac{a}{\sin A} \end{align*}より
\begin{align*} \quad R=\frac{a}{2\sin B} \end{align*}$a=2\sqrt{6} \ , \ A=120^{\circ}$ より
\begin{align*} \quad R &=\frac{2\sqrt{6}}{2\sin 120^{\circ}} \\[ 7pt ] &= \frac{2\sqrt{6}}{2 \cdot \frac{\sqrt{3}}{2}} \\[ 7pt ] &= \frac{2\sqrt{6}}{\sqrt{3}} \\[ 7pt ] &= 2\sqrt{2} \end{align*}立式できたら、ミスのないように計算します。ここでも、分数の分母に分数が出てきます。ただし、解答例のように、等式を変形した後に値を代入すると、分数をひっくり返す作業が不要になります。
問１(2)のポイントと解答例をまとめると以下のようになります。
分数の中に分数がある計算は、意外と頻繁に出てきます。扱いに慣れておきましょう。
次に、余弦定理を扱った問題を解いてみましょう。