数と式|整式の展開に関する問題を解いてみよう

乗法公式は、式の形や符号などの共通点や相違点に注目すれば、効率良く覚えることができます。しかし覚えただけで満足してはいけません。
実際の問題に当てはめて使えるかを確認しましょう。演習することで、どのような問題に、どの乗法公式を使うのかが分かってきます。
公式は使えてこそ
公式は使えてこそ価値があります。乗法公式は計算の負担を減らすためにあるので、どんどん使っていきましょう。
展開することだけを目的にすれば、使い慣れた分配法則で展開しても良いのですが、それでは乗法公式を使いこなせるようになりません。
今までのやり方に頼るだけでなく、新しいやり方で解決できるようにしておくことも大切ではないかと思います。
初めのうちは失敗することもあるでしょうが、大事なことは「とにかく使ってみる」ということです。
見ながらでも構わないので、使いこなせるまで演習をこなしましょう。
整式を展開してみよう
次の例題を解いてみましょう。
例題
次の整式を展開せよ。
\begin{align*} &1. \quad \left(3x+2 \right)^2 \\[ 7pt ] &2. \quad \left(x+4 \right)\left(x-4 \right) \\[ 7pt ] &3. \quad \left(x-3 \right)\left(x+5 \right) \\[ 7pt ] &4. \quad \left(2x+3 \right)\left(x-4 \right) \end{align*}式の形をよく見て、どの乗法公式で展開できそうかを考えます。問題を解くとき、与式をよく観察することが大切です。式を見て扱い方が決まることが多いので、式の形にはいつも注目しましょう。
例題1~3は中学レベルの問題なので今さらですが、このような易しいレベルから公式に当てはめる練習をすることで、公式の使い方が分かってきます。
レベルが上がるにつれて、下準備や処理することが多くなり、余裕がなくなります。易しくて負担が少ない問題から始めて、公式の正しい使い方をマスターしましょう。
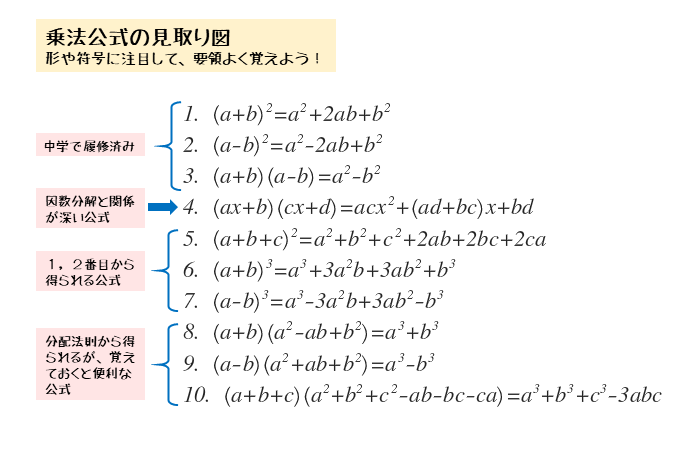
覚えておきたい乗法公式は10個あります。
例題1の解答・解説
例題1
次の整式を展開せよ。
\begin{align*} \quad \left(3x+2 \right)^2 \end{align*}与式を見ると非常に分かりやすい形です。2項からなる多項式を2乗した形なので、1番目の乗法公式に当てはまります。
与式と乗法公式を上下に並べて書き、各項の対応関係を確認します。
公式と与式の対応関係
\begin{align*} &\quad \left(a+b \right)^2 \\[ 7pt ] &\quad \left(3x+2 \right)^2 \end{align*}$2$ つの式を比べると
\begin{align*} &\quad a=3x \\[ 7pt ] &\quad b=2 \end{align*}与式に続く形で展開後の式を書きます。このとき、慣れるまでは対応する箇所を置き換えただけの式を書きましょう。公式に当てはめる練習をするためです。
例題1の展開
\begin{align*} \left(a+b \right)^2 &= a^2 +2ab +b^2 \\[ 10pt ] \left(3x+2 \right)^2 &= \left(3x \right)^2 + 2 \cdot 3x \cdot 2 +2^2 \end{align*}式を展開すると、和の形(式全体で1つの多項式)になっているので、各項ごとに乗算して整理します。解答例は以下のようになります。
例題1の考え方と解答例
\begin{align*} \text{与式} \quad \left(3x+2 \right)^2 \end{align*}考え方
\begin{align*} \left(a+b \right)^2 = a^2 +2ab +b^2 \end{align*}と与式を比べると
\begin{align*} &\quad a=3x \\[ 7pt ] &\quad b=2 \end{align*}に置き換えればよい。
解答例
\begin{align*} \quad &\left(3x+2 \right)^2 \\[ 7pt ] = \ &\left(3x \right)^2 +2 \cdot 3x \cdot 2+2^2 \\[ 7pt ] = \ &9x^2 +12x+4 \end{align*}公式の使い方に慣れてくると、数や文字が変わっても対応関係を簡単に見抜けるようになります。そのためにも演習して習熟度を上げましょう。
例題2の解答・解説
例題2
次の整式を展開せよ。
\begin{align*} \quad \left(x+4 \right) \left(x-4 \right) \end{align*}与式を見ると、これも非常に分かりやすいです。2項目の符号が異なる形なので、3番目の乗法公式に当てはまります。
与式と乗法公式を上下に並べて書き、各項の対応関係を確認します。
公式と与式の対応関係
\begin{align*} &\quad \left(a+b \right)\left(a-b \right) \\[ 7pt ] &\quad \left(x+4 \right)\left(x-4 \right) \end{align*}$2$ つの式を比べると
\begin{align*} &\quad a=x \\[ 7pt ] &\quad b=4 \end{align*}与式に続く形で展開後の式を書きます。
例題2の展開
\begin{align*} \left(a+b \right)\left(a-b \right) &= a^2 -b^2 \\[ 10pt ] \left(x+4 \right)\left(x-4 \right) &= x^2 -4^2 \end{align*}展開後は和の形になっているので、各項ごとに整理すると終了です。解答例は以下のようになります。
例題2の考え方と解答例
\begin{align*} \text{与式} \quad \left(x+4 \right)\left(x-4 \right) \end{align*}考え方
\begin{align*} \left(a+b \right)\left(a-b \right) = a^2 -b^2 \end{align*}と与式を比べると
\begin{align*} &\quad a=x \\[ 7pt ] &\quad b=4 \end{align*}に置き換えればよい。
解答例
\begin{align*} \quad &\left(x+4 \right)\left(x-4 \right) \\[ 7pt ] = \ &x^{\scriptsize{2}}-4^2 \\[ 7pt ] = \ &x^{\scriptsize{2}}-16 \end{align*}乗法公式の中で最も分かりやすい形です。
例題3の解答・解説
例題3
次の整式を展開せよ。
\begin{align*} \quad \left(x-3 \right) \left(x+5 \right) \end{align*}与式を見ると、文字xについての1次式どうしの積になっています。4番目の乗法公式を利用できます。
もちろん、中学で履修済みの公式でも展開できますが、xの1次の項の係数が1になるとは限らないので、できるだけ4番目の乗法公式を使って展開しましょう。
与式と乗法公式を上下に並べて書き、各項の対応関係を確認します。公式のbとの対応関係を間違えやすいので注意しましょう。
公式と与式の対応関係
\begin{align*} &\quad \left(ax+b \right)\left(cx+d \right) \\[ 7pt ] &\quad \left(x-3 \right)\left(x+5 \right)=\left\{x+ \left(-3 \right) \right\}\left(x+5 \right) \end{align*}$2$ つの式を比べると
\begin{align*} &\quad a=1 \\[ 7pt ] &\quad b=-3 \\[ 7pt ] &\quad c=1 \\[ 7pt ] &\quad d=5 \end{align*}与式に続く形で展開後の式を書きます。
例題3の展開
\begin{align*} \left(ax+b \right)\left(cx+d \right) &= acx^2 +\left(ad+bc \right)x +bd \\[ 10pt ] \left(x-3 \right)\left(x+5 \right) &= 1 \cdot 1 \cdot x^2 +\left\{1 \cdot 5 + \left(-3 \right) \cdot 1 \right\}x + \left(-3 \right) \cdot 5 \end{align*}展開後は各項ごとに処理すると終了です。符号ミスに気を付けましょう。解答例は以下のようになります。
例題3の考え方と解答例
\begin{align*} \text{与式} \quad \left(x-3 \right)\left(x+5 \right)=\left\{x+\left(-3 \right) \right\}\left(x+5 \right) \end{align*}考え方
\begin{align*} \left(ax+b \right)\left(cx+d \right) = acx^2 +\left(ad+bc \right)x +bd \end{align*}と与式を比べると
\begin{align*} &\quad a=1 \\[ 7pt ] &\quad b=-3 \\[ 7pt ] &\quad c=1 \\[ 7pt ] &\quad d=5 \end{align*}に置き換えればよい。
解答例
\begin{align*} \quad &\left(x-3 \right)\left(x+5 \right) \\[ 7pt ] = \ &1 \cdot 1 \cdot x^2 +\left\{1 \cdot 5 + \left(-3 \right) \cdot 1 \right\}x + \left(-3 \right) \cdot 5 \\[ 7pt ] = \ &x^2 +2x-15 \end{align*}例題4の解答・解説
例題4
次の整式を展開せよ。
\begin{align*} \quad \left(2x+3 \right)\left(x-4 \right) \end{align*}与式を見ると、例題3と同様にxについての1次式どうしの積になっているので、4番目の乗法公式で展開できます。
与式と乗法公式を上下に並べて書き、各項の対応関係を確認します。公式のdとの対応関係を間違えやすいので注意しましょう。
公式と与式の対応関係
\begin{align*} &\quad \left(ax+b \right)\left(cx+d \right) \\[ 7pt ] &\quad \left(2x+3 \right)\left(x-4 \right)=\left(2x+3 \right)\left\{x+ \left(-4 \right) \right\} \end{align*}$2$ つの式を比べると
\begin{align*} &\quad a=2 \\[ 7pt ] &\quad b=3 \\[ 7pt ] &\quad c=1 \\[ 7pt ] &\quad d=-4 \end{align*}与式に続く形で展開後の式を書きます。
例題4の展開
\begin{align*} \left(ax+b \right)\left(cx+d \right) &= acx^2 +\left(ad+bc \right)x +bd \\[ 10pt ] \left(2x+3 \right)\left(x-4 \right) &= 2 \times 1 \times x^2 +\left\{2 \times \left(-4 \right) + 3 \times 1 \right\}x + 3 \times \left(-4 \right) \end{align*}展開後は各項ごとに処理すると終了です。符号ミスに気を付けましょう。解答例は以下のようになります。
例題4の考え方と解答例
\begin{align*} \text{与式} \quad \left(2x+3 \right)\left(x-4 \right)=\left(2x+3 \right)\left\{x+\left(-4 \right) \right\} \end{align*}考え方
\begin{align*} \left(ax+b \right)\left(cx+d \right) = acx^2 +\left(ad+bc \right)x +bd \end{align*}と与式を比べると
\begin{align*} &\quad a=2 \\[ 7pt ] &\quad b=3 \\[ 7pt ] &\quad c=1 \\[ 7pt ] &\quad d=-4 \end{align*}に置き換えればよい。
解答例
\begin{align*} \quad &\left(2x+3 \right)\left(x-4 \right) \\[ 7pt ] = \ &2 \cdot 1 \cdot x^2 +\left\{2 \cdot \left(-4 \right) + 3 \cdot 1 \right\}x + 3 \cdot \left(-4 \right) \\[ 7pt ] = \ &2x^2 -5x-12 \end{align*}要領を掴めたら、各項の係数や定数項を暗算して、一気に展開できるようにしよう。
次は応用問題に挑戦してみましょう。