数学２
三角形の重心の座標を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
\begin{align*}
&(1) \quad \text{$\triangle {ABC}$ の重心を $G$、辺 $BC$ の中点を $L$、辺 $CA$ の中点を $M$ とする。} \\[ 5pt ]
&\qquad \qquad A(6 \ , \ 6) \ , \ M(7 \ , \ 4) \ , \ G \left(\frac{16}{3} \ , \ \frac{8}{3} \right) \\[ 7pt ]
&\qquad \text{であるとき、点 $B \ , \ L$ の座標をそれぞれ求めよ。} \\[ 10pt ]
&(2) \quad \text{$3$ 点 $A(7 \ , \ 6) \ , \ B(-3 \ , \ 1) \ , \ C(8 \ , \ 1)$ に対して、辺 $BC$ の中点を $P$、} \\[ 5pt ]
&\qquad \text{辺 $CA$ を $3:2$ に外分する点を $Q$、辺 $AB$ を $3:2$ に内分する点を} \\[ 5pt ]
&\qquad \text{$R$ とする。このとき、$\triangle {PQR}$ の重心の座標を求めよ。}
\end{align*}
問(1)の解答・解説
問(1)
\begin{align*}
&\text{$\triangle {ABC}$ の重心を $G$、辺 $BC$ の中点を $L$、辺 $CA$ の中点を $M$ とする。} \\[ 5pt ]
&\quad A(6 \ , \ 6) \ , \ M(7 \ , \ 4) \ , \ G \left(\frac{16}{3} \ , \ \frac{8}{3} \right) \\[ 7pt ]
&\text{であるとき、点 $B \ , \ L$ の座標をそれぞれ求めよ。}
\end{align*}
三角形の頂点のうち、座標が分かっているのは点Ａだけです。概略だけでも作図しておくと、取り組みやすくなります。
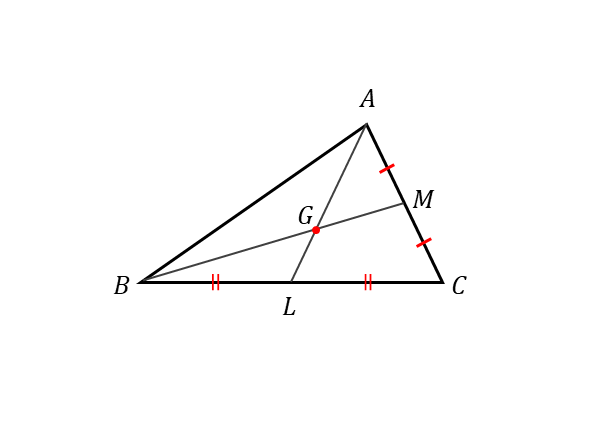問(1)の作図 重心Ｇや中点Ｍの座標を表すには、頂点Ｂ，Ｃの座標が必要なので定義しておきます。
辺ＡＣの中点Ｍの座標が与えられているので、２点Ａ，Ｃの座標を用いて方程式を導きます。
問(1)の解答例 1⃣
\begin{align*}
&\text{$B \ , \ C$ の座標を $B(a \ , \ b) \ , \ (c \ , \ d)$ とする。} \\[ 5pt ]
&\text{辺 $CA$ の中点 $M$ の座標が $(7 \ , \ 4)$ であるので} \\[ 5pt ]
&\quad \frac{c+6}{2}=7 \\[ 7pt ]
&\quad \frac{d+6}{2}=4 \\[ 7pt ]
&\text{これを解くと} \\[ 5pt ]
&\quad c=8 \ , \ d=2 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad C \ (8 \ , \ 2)
\end{align*}
点Ｃの座標を求めることができました。中点の座標から、線分の端にある点の座標を求めることができます。
中点の座標は、線分の両端の点の座標を用いて表される。
⇒ 中点と線分の片端の点の座標から、残りの端の座標についての方程式を導くことができる
次に、点Ｂの座標を求めます。△ＡＢＣの重心Ｇの座標が与えられています。△ＡＢＣの３つの頂点Ａ，Ｂ，Ｃの座標を用いて方程式を導きます。
問(1)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad C \ (8 \ , \ 2) \\[ 7pt ]
&\text{$\triangle {ABC}$ の重心 $G$ の座標より} \\[ 5pt ]
&\quad \frac{6+a+8}{3}=\frac{16}{3} \\[ 7pt ]
&\quad \frac{6+b+2}{3}=\frac{8}{3} \\[ 7pt ]
&\text{これを解くと} \\[ 5pt ]
&\quad a=2 \ , \ b=0 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad B \ (2 \ , \ 0)
\end{align*}
点Ｂの座標を求めることができました。重心の座標から、頂点の座標を求めることができます。
重心の座標は、３つの頂点の座標を用いて表される。
⇒ 重心と２つの頂点の座標から、残りの頂点の座標についての方程式を導くことができる
さいごに、辺ＢＣの中点Ｌの座標を求めます。２点Ｂ，Ｃの座標を用います。
問(1)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad C \ (8 \ , \ 2) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad B \ (2 \ , \ 0) \\[ 7pt ]
&\text{辺 $BC$ の中点 $L$ の座標は} \\[ 5pt ]
&\quad \left( \frac{2+8}{2} \ , \ \frac{0+2}{2} \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad L \ (5 \ , \ 1)
\end{align*}
中点や重心の座標から方程式を導くことによって、要求された座標を求めます。中点なら線分の両端の座標が必要です。また、重心なら三角形の３つの頂点の座標が必要です。そのために、点Ｂ，Ｃの座標を先に定義しています。
問(2)の解答・解説
問(2)
\begin{align*}
&\text{$3$ 点 $A(7 \ , \ 6) \ , \ B(-3 \ , \ 1) \ , \ C(8 \ , \ 1)$ に対して、辺 $BC$ の中点を $P$、} \\[ 5pt ]
&\text{辺 $CA$ を $3:2$ に外分する点を $Q$、辺 $AB$ を $3:2$ に内分する点を} \\[ 5pt ]
&\text{$R$ とする。このとき、$\triangle {PQR}$ の重心の座標を求めよ。}
\end{align*}
座標平面上に正確に図示した方が良いですが、概略図でも構いません。とにかくイメージしやすく作図しましょう。入試で困らないように、しっかり訓練しておきましょう。
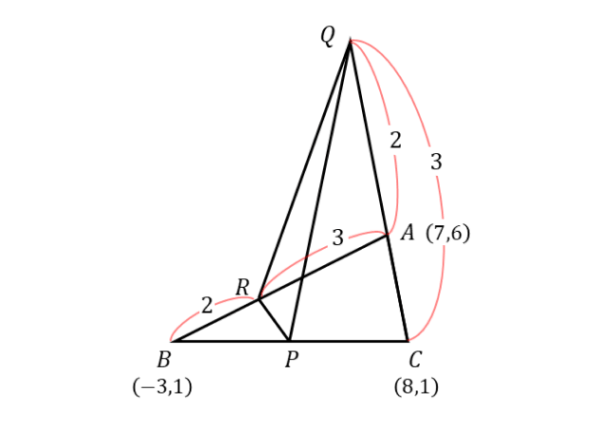問(2)の作図 △ＡＢＣの３つの頂点の座標が分かっているので、どちらかと言うと取り組みやすい問題です。公式を上手に利用して解きましょう。
△ＰＱＲの重心の座標を求めるためには、３つの頂点Ｐ，Ｑ，Ｒの座標が必要です。点Ａ，Ｂ，Ｃの座標ではないことに注意しましょう。
点Ｐ，Ｑ，Ｒの座標をそれぞれ求めます。３点Ａ，Ｂ，Ｃの座標を中点、内分点、外分点の公式に代入します。
問(2)の解答例 1⃣
\begin{align*}
&\text{辺 $BC$ の中点 $P$ の座標は} \\[ 5pt ]
&\quad \left( \frac{(-3)+8}{2} \ , \ \frac{1+1}{2} \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad P \ \left(\frac{5}{2} \ , \ 1 \right) \\[ 7pt ]
&\text{また、辺 $CA$ の外分点 $Q$ の座標は} \\[ 5pt ]
&\quad \left( \frac{(-2) \cdot 8+3 \cdot 7}{3-2} \ , \ \frac{(-2) \cdot 1+3 \cdot 6}{3-2} \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad Q \ (5 \ , \ 16) \\[ 7pt ]
&\text{さらに、辺 $AB$ の内分点 $R$ の座標は} \\[ 5pt ]
&\quad \left( \frac{2 \cdot 7+3 \cdot (-3)}{3+2} \ , \ \frac{2 \cdot 6+3 \cdot 1}{3+2} \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad R \ (1 \ , \ 3)
\end{align*}
△ＰＱＲの３つの頂点Ｐ，Ｑ，Ｒの座標が分かったので、重心の座標を求めます。
問(2)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad P \ \left(\frac{5}{2} \ , \ 1 \right) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad Q \ (5 \ , \ 16) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad R \ (1 \ , \ 3) \\[ 7pt ]
&\text{$\triangle {PQR}$ の重心の $x$ 座標は} \\[ 5pt ]
&\quad \frac{\frac{5}{2}+5+1}{3}=\frac{5+10+2}{2 \cdot 3}=\frac{17}{6} \\[ 7pt ]
&\text{また、重心の $y$ 座標は} \\[ 5pt ]
&\quad \frac{1+16+3}{3}=\frac{20}{3} \\[ 7pt ]
&\text{よって、$\triangle {PQR}$ の重心の座標は} \\[ 5pt ]
&\quad \left(\frac{17}{6} \ , \ \frac{20}{3} \right)
\end{align*}
分子に分数があるので、計算ミスに気を付けましょう。分母と分子にそれぞれ２を掛けて計算します。
外分点を扱った問題は内分点に比べて少ないので、外分点の作図を苦手とする人が意外と多いです。ですから、外分点を扱った問題では、出来る出来ないの差がかなり出ます。
外分点の表し方は、外分比に応じて２通りあります。しっかり書き分けできるようにしておきましょう。
Recommended books
メタ認知のためにも演習をこなすことは大切です。はじめのうちは何事も質よりも量の方を意識してこなす方が良いと思います。全体を一度通ってから質を考えると効率が良いでしょう。
特に、思考力を問われる問題の比重が過去に比べて増えてきています。パターンの暗記だけでは対応できなくなってきています。
オススメその１
そこで紹介するのが河合塾シリーズの『これからの大学入試に必要な数学の「思考力」を鍛える問題集』です。
河合塾数学科の考える「思考力・判断力・表現力」をまとめ、これに基づいて過去の入試問題を分析し、その中から思考力を養うために経験しておきたい問題を収集し解答・解説を収録。また、思考調査の問題を参考にして「共通テスト型問題」を作成。
センター試験から共通テストへと変わったことにより、「思考力・判断力・表現力」を問う問題が今まで以上に出題されると考えられます。これらは短期間で習得するのはなかなか難しいものです。日頃から訓練して身に付けるものなので、このような教材を利用してできるだけ早く取り組みたいところです。
オススメその２
バカロレア試験は、フランスの大学入学資格試験です。論述試験が中心です。思考力はもとより表現力も必要な試験です。
思考力・表現力を保障するには、大学教育の準備学力として、大学入試でどのような思考力・表現力を問うべきか。思考力・表現力を評価する論述型大学入試の実現に何が必要か。この思考力・表現力を中学校、高校でいかに育むべきか。本書では、論述試験中心のフランスの大学入学資格試験・バカロレア試験の問題や模範解答、採点規準、フランスの学校での授業観察などをもとに、これらの問いへのヒントを示す。第一人者が結集して執筆した、バカロレア研究の最前線。
海外に留学したいと考えている人にはおすすめです。思考力や表現力を短期間で養成するのは簡単ではありません。ですから、出来るだけ早く、意識的に取り組んでおいた方が良いでしょう。
さいごにもう一度まとめ
- 中点は２点の座標の平均。
- 重心は３点の座標の平均。
- 内分点や外分点の座標を求めるとき、比の扱いに気を付けよう。
- 外分点の取り方にはくれぐれも注意しよう。
