図形と計量｜三角比の方程式について
今回は、三角比の方程式について学習しましょう。これまでの履修内容で角と三角比とを対応付けることができていれば、スムーズに行きます。
もし、角に対する三角比がすぐに出てこない人は、もう一度演習してからの方が良いかもしれません。
三角比の方程式の解法
「三角比の方程式」と言うくらいですから、三角比が使われた方程式になります。
方程式の中に三角比が使われると、これまでの方程式とどこが違うのか、そういったところに注目して学習しましょう。
三角比の方程式では未知の変数は角θ
これまでの単元では、角に対する三角比を考えてきました。角の情報が決まれば、直角三角形が決まり、辺の関係もおのずと決まります。そうやって角の情報をもとに三角比を求めました。
三角比の方程式では、未知の変数は角θです。ですから三角比に対する角θを考えるのが、三角比の方程式でのポイントになります。
これまでとは逆の思考になるので、角と三角比の対応関係が把握できていないと、まだ難しく感じるかもしれません。
しかし、作図によってカバーできるので、諦めずに取り組みましょう。
三角比の方程式を解くことは角θを求めること
三角比に対する角を考えるので、三角比の方程式の解は角θです。
「三角比の方程式を解く」とは、正弦・余弦・正接などの三角比から角θを求めることです。
三角比の方程式を解く
- （三角比の方程式を解く）＝（三角比から角θを求める）
- （三角比の方程式の解）＝（角θ）
三角比の使い方が大切
三角比の情報から角θを求めますが、情報を上手に使って三角比の方程式を解いていきます。
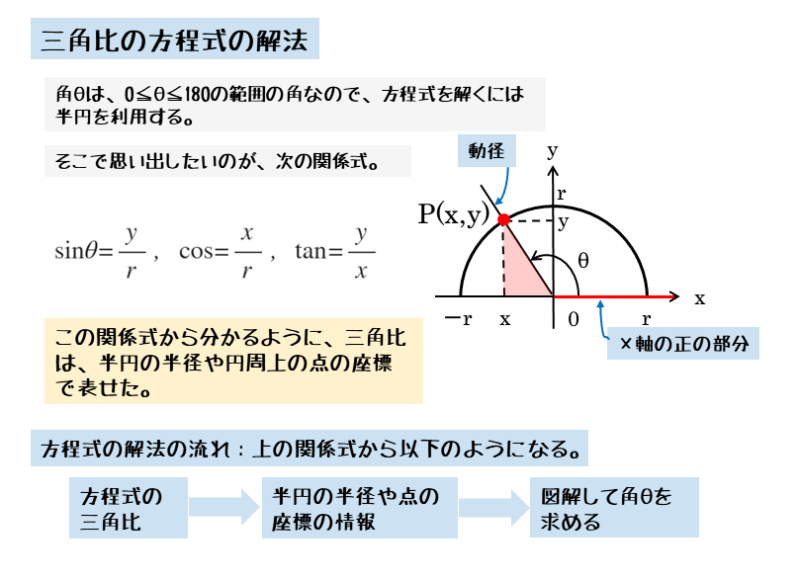
ここでは、求めたい角θは０°≦θ≦１８０°を満たす角なので、三角形は直角三角形に限りません。そのために三角比の拡張を利用します。
三角比の拡張を利用するには、座標平面に円と点を作図します。この図をもとにして、方程式を解きます。
作図するには円の半径や円周上の点の座標を必要としますが、これらは方程式で与えられた三角比から知ることができます。それらをもとに作図すれば、角θを可視化することができます。
三角比の方程式を解く流れ
- 与えられた方程式から、半径ｒや点Ｐの座標を得る
- 得た情報をもとに作図する
- 作図から角θを求める
三角比の方程式は計算によって解くと言うよりも、むしろ作図によって図解すると言った方が適切。一応、平面図形の単元なので作図は必須と考えておこう。
三角比の方程式を解いてみよう
次の問題を解いてみましょう。ただし、０°≦θ≦１８０°です。
正弦・余弦・正接の方程式を一通り用意したので、これで共通点や相違点を確認しながらマスターしましょう。
問１の解答・解説
問１
$0^{\circ} \leqq \theta \leqq 180^{\circ}$ のとき、次の等式を満たす $\theta$ を求めよ。
\begin{align*} \quad \sin \theta = \frac{1}{2} \end{align*}問１は正弦を用いた方程式です。言葉にすれば「正弦が１/２になる角θは？」という問題です。角に対する三角比を求めていたこれまでとは逆であることが分かります。
三角比の方程式を解くとき、答案自体はほとんど記述しません。むしろ、その前の準備や作図（下図参照）に時間を掛けます。ここがしっかりできれば、三角比の方程式を解くことはそれほど難しくありません。
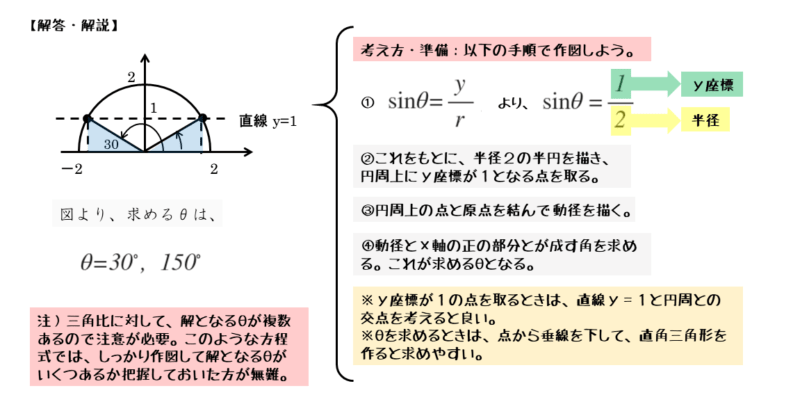
三角比の値１/２から円の半径や点の座標に関する情報を取り出します。三角比の拡張で学習した式を利用します。
三角比の拡張
円の半径を $r$、円周上の点 $P$ の座標を $(x \ , \ y)$ とすると
\begin{align*} &\quad \sin \theta = \frac{y}{r} \\[ 7pt ] &\quad \cos \theta = \frac{x}{r} \\[ 7pt ] &\quad \tan \theta = \frac{y}{x} \end{align*}与式と公式を見比べると、円の半径は２、点Ｐのｙ座標は１であることが分かります。
得た情報をもとに作図します。
まず、座標平面に半径２の円を描きます。
次に、円周上にあり、ｙ座標が１である点を作ります。
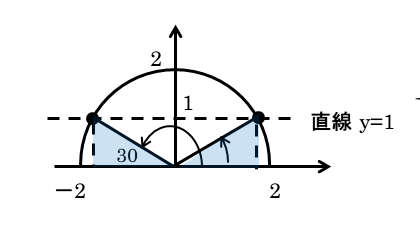
ｙ座標が１となる点は、直線ｙ＝１上にあることを利用します。円と直線ｙ＝１との交点が作りたい点になります。
交点は円周上に２つできます。それぞれの交点と原点とを結ぶと動径ができます。この動径とｘ軸の正の部分とのなす角が、方程式の解である角θとなります。
図から角θの値を求めます。できるだけ正確に作図すると、角θの大きさが一目で分かります。方程式を満たすθの値は、３０°，１５０°になります。
問１のポイントと解答例をまとめると以下のようになります。
０°≦θ≦１８０°の範囲では、正弦（ｓｉｎ）の値が正の数になる角は２つある。三角比の方程式の解は、基本的に２つあると考えておこう。しっかり作図をして視覚化しよう。
問２の解答・解説
問２
$0^{\circ} \leqq \theta \leqq 180^{\circ}$ のとき、次の等式を満たす $\theta$ を求めよ。
\begin{align*} \quad \cos \theta = -\frac{1}{2} \end{align*}問２は余弦を用いた方程式です。言葉にすれば「余弦が－１/２になる角θは？」という問題です。
余弦が負の数であることを考慮して、扱いやすい形に変形します。
与式を変形する
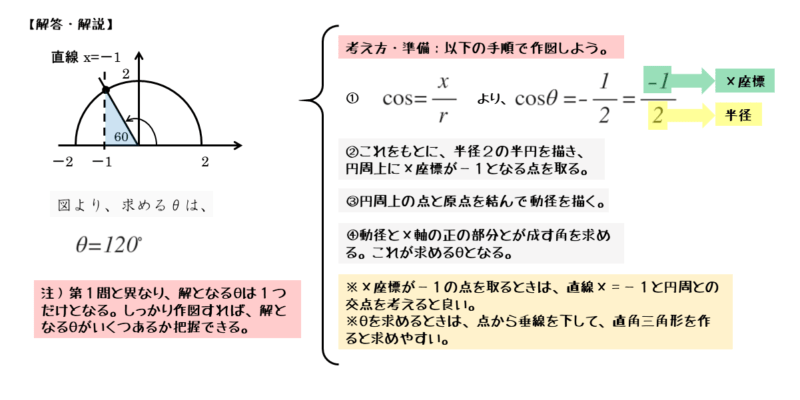
\begin{align*} \quad \cos \theta = \frac{x}{r} \end{align*}に合わせて与式を変形する。
\begin{align*} \quad \cos \theta &= -\frac{1}{2} \\[ 7pt ] &= \frac{-1}{2} \end{align*}与式において、右辺の分子を１から－１に変形しました。与式と公式を見比べると、円の半径は２、点Ｐのｘ座標は－１であることが分かります。
得た情報をもとに作図します。
まず、座標平面に半径２の円を描きます。
次に、円周上にあり、ｘ座標が－１である点を作ります。
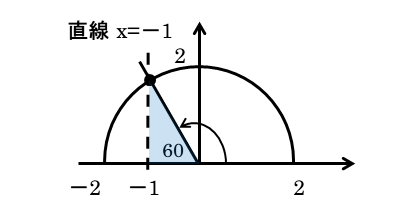
ｘ座標が－１となる点は、直線ｘ＝－１上にあることを利用します。円と直線ｘ＝－１との交点が作りたい点になります。
交点は円周上に１つできます。交点と原点とを結ぶと動径ができます。この動径とｘ軸の正の部分とのなす角が、方程式の解である角θとなります。
図から角θの値を求めます。できるだけ正確に作図すると、角θの大きさが一目で分かります。方程式を満たすθの値は１２０°になります。
問２のポイントと解答例をまとめると以下のようになります。
０°≦θ≦１８０°の範囲では、余弦（ｃｏｓ）の値が負の数になる角は１つだけ。しっかり作図をして視覚化しよう。
問３の解答・解説
問３
$0^{\circ} \leqq \theta \leqq 180^{\circ}$ のとき、次の等式を満たす $\theta$ を求めよ。
\begin{align*} \quad \tan \theta = -1 \end{align*}問３は正接を用いた方程式です。言葉にすれば「正接が－１になる角θは？」という問題です。
正接が負の整数であることを考慮して、扱いやすい形に変形します。
与式を変形する
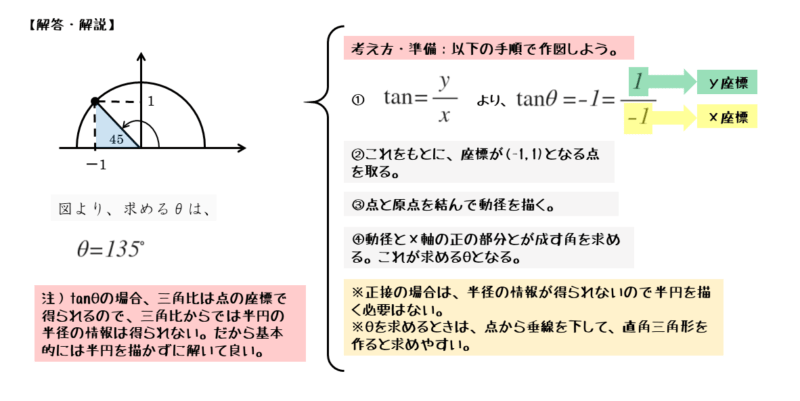
\begin{align*} \quad \tan \theta = \frac{y}{x} \end{align*}に合わせて与式を変形する。
\begin{align*} \quad \tan \theta &= -1 \\[ 7pt ] &= \frac{1}{-1} \end{align*}整数のままだと、円の半径や点の座標の情報を得にくいので、与式の右辺を分数で表します。
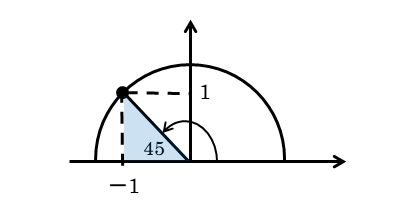
正接はｘ座標とｙ座標で表されます。ここで、半円を用いるので、ｙ≧０であることを考慮します。ｙ座標が正の数、ｘ座標が負の数になるように変形します。
与式と公式を見比べると、点Ｐの座標は(－１，１)であることが分かります。残念ながら、円の半径を知ることはできません。
０°≦θ≦１８０°の範囲では、ｙ座標が負の数になる点は存在しないので、ｘ座標が負の数になるように変形しよう。三角比の拡張を思い出そう。
正接を用いた方程式では、円の半径が分からないので、正弦や余弦とは少し違った作図をします。
円の半径が分かりませんが、とりあえず円を描きます。
次に、座標(－１，１)である点を作ります。図では円周上に作っていますが、点(－１，１)が円周上になくても問題ありません。
作った点と原点とを結ぶと動径ができます。もし、点(－１，１)が円周上になければ、円と動径との交点が新たにできます。
動径とｘ軸の正の部分とのなす角が、方程式の解である角θです。円と動径との交点は１つできるので、方程式の解は１つです。
図から角θの値を求めます。できるだけ正確に作図すると、角θの大きさが一目で分かります。方程式を満たすθの値は１３５°になります。
問３のポイントと解答例をまとめると以下のようになります。
なお、正接を用いた方程式では、円を作図せずに解くこともあります。また、問３の別解として、θの範囲によりますが、正接の定義を応用して、単位円（半径１の円）を利用して解く解法もあります。
Recommended books
図形の問題は、気付けないと全くと言って良いほど手も足も出なくなります。気付けるかどうかはやはり日頃から作図したり、図形を色んな角度から眺めたりすることだと思います。
そのためにもやはり演習量は大切です。はじめのうちは何事も質よりも量の方を意識してこなす方が良いと思います。全体を一度通ってから質を考えると効率が良いでしょう。
演習をこなすとなると、単元別になった教材を使って集中的にこなすと良いでしょう。網羅型でも良いですが、苦手意識のある単元であれば、単元別に特化した教材の方が良いかもしれません。
オススメその１
分野ごとに押さえていくのに役立つのは『高速トレーニング』シリーズです。三角関数、ベクトル、数列などの分野もあります。
ここで紹介するのは『数学１高速トレーニング 三角比編』です。
三角比に苦手意識のある人にとって、躓きやすいところを解説してあるので良い教材だと思います。基礎の定着に向いた教材です。
これで自信がついたら、チャートなどのもう少し難易度の高い問題を扱った教材に取り組むと良いでしょう。三角比は三角関数に関わるので、ここでしっかりマスターしておきましょう。
オススメその２
『改訂版 坂田アキラの三角比・平面図形が面白いほどわかる本』もおすすめです。
計算過程が省略されず、丁寧に記述されているので、計算の途中で躓くこともほとんどないでしょう。苦手な人や初学者にとって良い補助教材になると思います。
坂田のビジュアル解説で最近流行りの空間図形までフォロー!
数学１「図形と計量」（いわゆる三角比）と数学Ａ「図形の性質」の基本事項をまとめ、それぞれの典型問題および融合問題の考え方・解き方がていねいに解説されています。
また、今回の改訂により、近年の大学入試（上位から下位まで幅広く）で頻出の空間図形の問題を厚くしました。
オススメその３
『中学入試 算数図形問題完全マスター』と『中学入試 算数図形問題完全マスター ハイレベル』は中学入試のための教材ですが、図形に苦手意識がある人にはちょうど良いかもしれません。
公立校の適性検査型入試問題を意識し、長文の問題や思考力・表現力を要する問題も収録されています。チャート式で有名な数研出版の教材なので、安心して取り組めるでしょう。
さいごに、もう一度、頭の中を整理しよう
- 三角比の方程式の解は角θの値。
- 三角比の情報から得た円の半径や点の座標をもとに作図して、角θを図形的に求める。
- 作図には、三角比の拡張で学習した三角比の関係式を利用する。
- 三角比に対する角θは１つとは限らず、複数あるときもある。