図形と計量|空間図形への応用について

「図形と計量」の最後は空間図形への応用です。
四角形や円などの平面図形と同じように、三角比に関する知識をいかに使いこなせるかが大切です。ここにきて身に付けていない知識があると滞ってしまいます。もちろん、図形に関する知識も必要に応じて利用しなければなりません。
これまでに身に付けた知識をどのように使うのかを意識しながら学習しましょう。記事の画像が見辛いときはクリックすると拡大できます。
空間図形について
空間図形とは、三次元の広がりをもった立体図形のことで、たとえば立方体や直方体などのことです。
高校では、四面体や六面体などの空間図形が扱われます。「~面体」は面の数で空間図形を区別する言い方ですが、その中でも4つの面がすべて正三角形である正四面体は頻出です。
ちなみに、立方体や直方体は、面を6つもつので六面体です。特に、立方体はすべての面が正方形になっているので、正六面体と言います。
これらの空間図形に対して三角比を使うわけですが、三角比でできることは辺の長さや角の大きさを求めたり、面積を求めたりするくらいです。辺の長さや面積が分かれば、空間図形の体積を求めることもできます。
基本的に辺の長さを求めるために三角比を使うので、あまり難しく考えないようにしましょう。
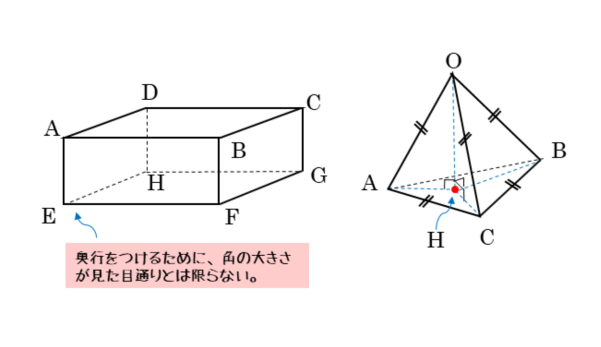
空間図形を作図するときの注意点
ただし、空間図形の難しいところは、3次元であるところです。作図を上手にしないと見誤ったり、気付かなかったりすることが平面図形のときよりも多くなります。
空間図形は奥行があるように描くので、特に角の大きさを見誤りやすくなります。ささいなミスをしないためには、自分なりのルールを決めて作図した方が良いでしょう。
作図するときの自分なりのルール(例)
- 長さが等しい辺には1カ所だけ数値を入れて、他は記号で済ます。
- 大きさが等しい角も同じ。
- 注目している面は抜き出して考える。
作図では長さが等しいことや平行であることを表す記号があります。そのような記号を上手に使うと、スッキリした作図ができます。
また、注目している面を抜き出して考えることは非常に効果的です。空間図形の問題では、「できる限り2次元に次元を落として考える」ことが大切です。
作図をしても何も得ることができない図では意味がない。自分なりのルールで役に立つ図を描こう。
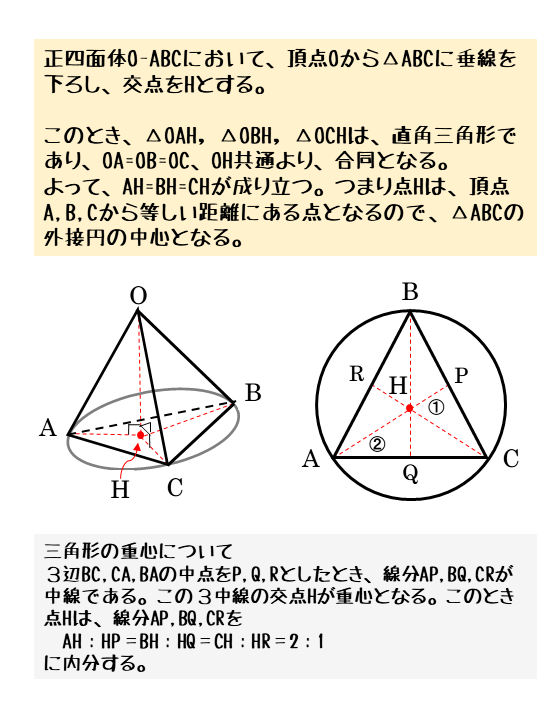
正四面体の垂線について
正四面体については先ほども触れましたが、もう少し詳しく確認しておきます。
この単元では、正四面体の体積を求めるまでを小問形式で出題されることが多く、その場合、正四面体の高さを求める必要があります。正四面体の高さは、頂点から底面に下ろした垂線の長さです。この垂線が底面のどこに下ろされるのかを知っておく必要があります。
正四面体の4つの面はすべて正三角形です。頂点から底面に垂線を下ろすと、垂線は底面の重心を通ります。この重心は、底面が正三角形であるので外接円の中心(外心)と一致します。
つまり、垂線は、底面の重心であり、外接円の中心でもある点で底面と交わります。
重心とは、三角形の3つの中線が交わる点で、すべての中線を2:1の比に分ける。中線とは、頂点と対辺の中点とを通る線分のこと。
正四面体の性質についてまとめると以下のようになります。問題を解くための予備知識として覚えておきましょう。
正四面体の性質(まとめ)
①正四面体とは、4つの面がすべて正三角形の三角錐のこと。
②正四面体において、頂点から対面に垂線を下ろしたとする。このとき、垂線と底面の交点は、底面の三角形の外接円の中心(外心)になる。
なお、正三角形の外接円の中心(外心)は、3本の中線の交点である重心と重なる。中線とは、頂点とその対辺の中点とを結んだ線分のこと。
垂線と底面との交点が外接円の中心になることの証明は、直角三角形の合同証明によって得られます。
言われてみると分かるのですが、自分で証明するとなると、一度は証明しておかないとなかなか難しいと思います。この単元の問題を解くときにきっと役に立つので、ぜひチャレンジしてみて下さい。
証明の例は以下のようになります。
次は、正四面体を扱った問題を解いてみましょう。
正四面体を扱った問題を解いてみよう。
次の問題を考えてみましょう。
設問全体に目を通すと、最後の問1(3)で正四面体の体積を求めますが、それまでの問題をきちんと解いていけば必、要な数量が揃っているはずです。計算ミスのないように注意しましょう。
問1(1)の解答・解説
問1(1)
$1$ 辺の長さが $\sqrt{3}$ である正四面体 $OABC$ において、頂点 $O$ から $\triangle ABC$ に垂線 $OH$ を下ろすとき、次のものを求めなさい。
$\quad AH$ の長さ
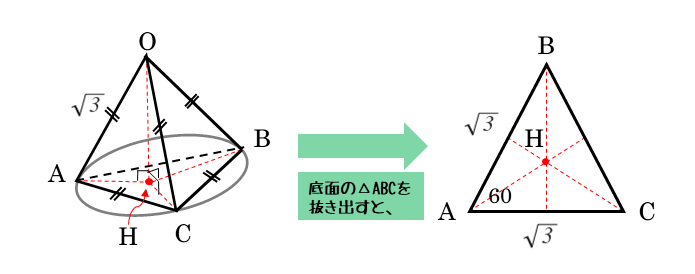
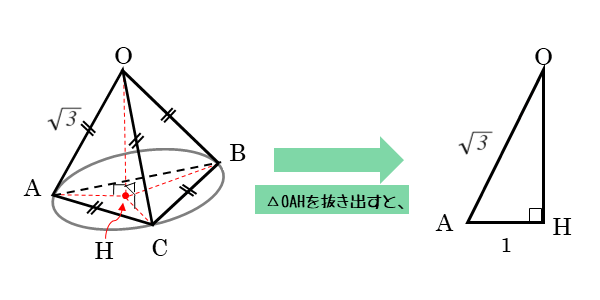
作図すると以下のような図が描けます。必要に応じて面を抜き出して、2次元で考えるようにします。
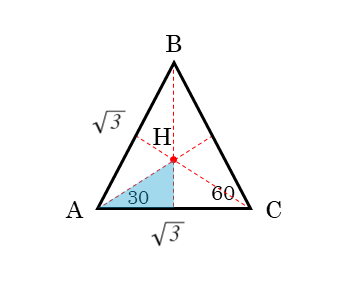
線分AHは、底面の△ABC上にあるので、△ABCを抜き出します。このとき、辺の長さや角の大きさなどを、立体のときよりも正確に作図しておきます。
この線分AHの長さは、点Hが△ABCの外接円の中心であることを知っていれば、外接円の半径に等しいことが分かります。「外接円の半径」が出てくれば正弦定理です。
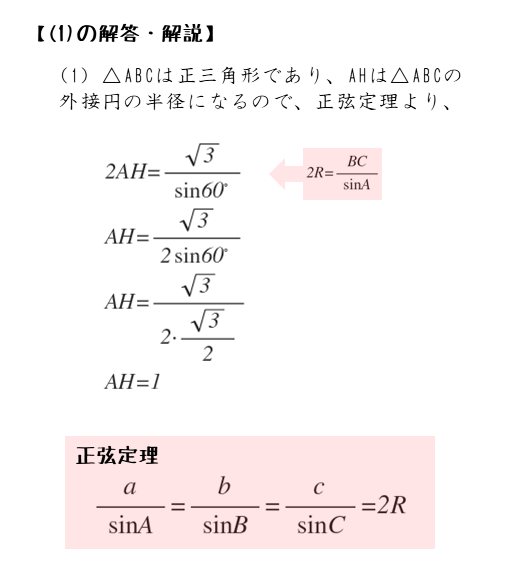
問1(1)の解答例
$\triangle ABC$ において、正弦定理より
\begin{align*} \quad 2R &= \frac{BC}{\sin {\angle BAC}} \\[ 7pt ] 2 \cdot AH &= \frac{\sqrt{3}}{\sin 60^{\circ}} \\[ 7pt ] AH &= \frac{\sqrt{3}}{2 \cdot \sin 60^{\circ}} \end{align*}式に数を代入した後はミスのないように計算します。解答例の続きは以下のようになります。
別解になりますが、△ABCが正三角形であることに注目してより図形的に解くこともできます。
△ABCの3つの中線はそれぞれが対辺の垂直二等分線であり、角の二等分線でもあります。このことを利用すると、三角比の定義だけで求めることもできます。
問1(1)の別解例
三角比の定義より
\begin{align*} \quad \cos 30^{\circ} &= \frac{\frac{1}{2}AC}{AH} \\[ 7pt ] AH &= \frac{1}{2} AC \cdot \frac{1}{\cos 30^{\circ}} \\[ 7pt ] AH &= \frac{\sqrt{3}}{2} \cdot \frac{2}{\sqrt{3}} \\[ 7pt ] AH &= 1 \end{align*}問1(2)の解答・解説
問1(2)
$1$ 辺の長さが $\sqrt{3}$ である正四面体 $OABC$ において、頂点 $O$ から $\triangle ABC$ に垂線 $OH$ を下ろすとき、次のものを求めなさい。
$\quad OH$ の長さ
問1(1)で、AH=1となることも考慮に入れます。
垂線OHは、底面の△ABCとは垂直の関係にあります。したがって第1問(1)で求めた線分AHを一辺にもつ△OAHは直角三角形です。
直角三角形では三平方の定理が成り立つので、それを利用して垂線OHの長さ、すなわち正四面体の高さを求めます。
問1(2)の解答例
$\triangle OAH$ において、三平方の定理より
\begin{align*} &\quad {OH}^{2} + {AH}^{2} = {OA}^{2} \\[ 7pt ] &\quad {OH}^{2} = {OA}^{2} – {AH}^{2} \end{align*}あとはこれを解くだけです。解答例の続きは以下のようになります。
立体の高さを三平方の定理で求める問題は頻出なので、三平方の定理を使えるようになっておきましょう。
問1(3)の解答・解説
問1(3)
$1$ 辺の長さが $\sqrt{3}$ である正四面体 $OABC$ において、頂点 $O$ から $\triangle ABC$ に垂線 $OH$ を下ろすとき、次のものを求めなさい。
正四面体 $OABC$ の体積 $V$
問1(1),(2)で、AH=1,OH=$\sqrt{2}$ となることも考慮に入れます。
正四面体の体積を求めるためには、体積の公式を考慮すると底面積が必要だと分かります。底面積は△ABCの面積です。
△ABCは正三角形なので内角はすべて60°であり、また3辺の長さも初めから分かっています。2辺とそのはさむ角の大きさが分かっているので、三角形の面積の公式を使って△ABCの面積を求めます。
問1(3)の解答例 1⃣
$\triangle ABC$ の面積を求めると
\begin{align*} \quad \triangle ABC &= \frac{1}{2} \cdot AB \cdot AC \cdot \sin A \\[ 7pt ] &= \frac{1}{2} \cdot \sqrt{3} \cdot \sqrt{3} \cdot \sin 60^{\circ} \\[ 7pt ] &= \frac{1}{2} \cdot \sqrt{3} \cdot \sqrt{3} \cdot \frac{\sqrt{3}}{2} \\[ 7pt ] &= \frac{3 \sqrt{3}}{4} \end{align*}正四面体の底面である△ABCの面積を求めたので、正四面体の体積Vを求めます。
問1(3)の解答例 2⃣
正四面体 $OABC$ の体積 $V$ を求めると
\begin{align*} \quad V = \frac{1}{3} \cdot \triangle ABC \cdot OH \end{align*}これまでに求めた値を代入して体積を求めます。解答例の続きは以下のようになります。
三角比を使うためには図形の定義や性質も知っておかなければなりません。
次は、直方体を扱った問題を解いてみましょう。