図形と計量|三角比の相互関係について その1

三角比の拡張によって、直角三角形の1つの鋭角について定義された三角比は、鈍角についても利用することができました。
今回は、正弦・余弦・正接の3つの相互関係について学習しましょう。三角比の相互関係が分かれば、三角比を使った式を変形することができるようになります。
記事の画像が見辛いときはクリックすると拡大できます。
三角比の相互関係
三角比には正弦・余弦・正接の3つの表し方があり、こららの関係のことを三角比の相互関係と言います。
三角比の相互関係はよく利用されるので、演習をこなして使えるようにしておきましょう。
正弦・余弦・正接の関係を表す式
三角比の相互関係は、正弦・余弦・正接の関係を表します。この関係は、三角比の拡張で学習したことを利用して導出されます。
もちろん、直角三角形(90°未満の角θ)の三角比で導出することもできます。
三角比の拡張
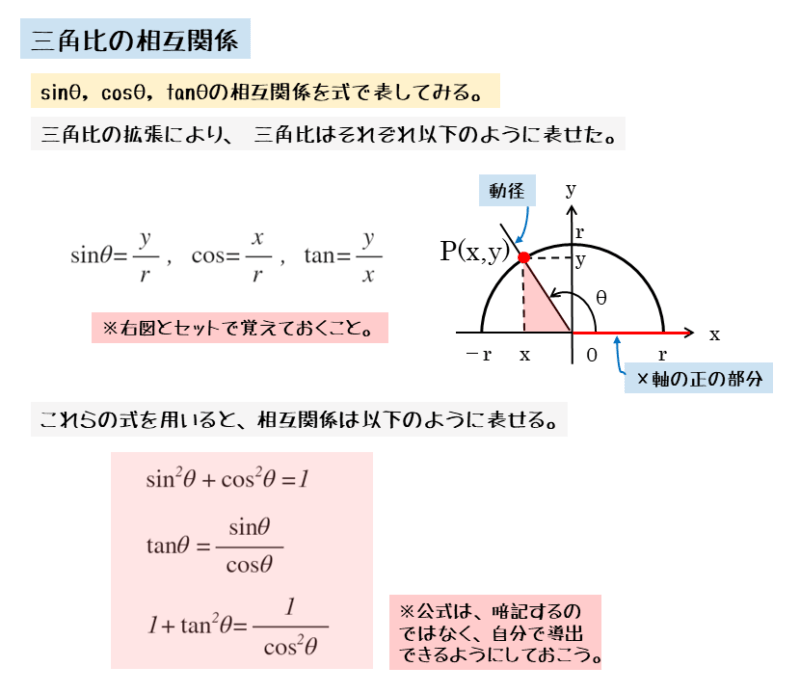
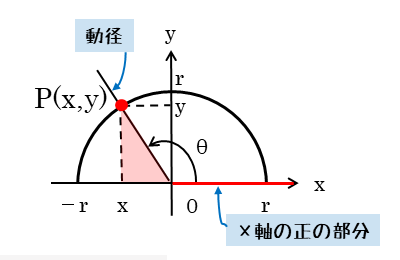
半径 $r$ の円周上に点 $P \ (x \ , \ y)$ があるとき
\begin{align*} \quad \sin \theta &= \frac{y}{r} \\[ 7pt ] \quad \cos \theta &= \frac{x}{r} \\[ 7pt ] \quad \tan \theta &= \frac{y}{x} \end{align*}これら3つの三角比を利用して、三角比の相互関係を導出します。三角比の相互関係を表す式はいくつかありますが、その中でも基本となるものが3つあります。
三角比の相互関係
\begin{align*} &\quad \sin^{2}{\theta} +\cos^{2}{\theta} =1 \\[ 7pt ] &\quad \tan{\theta} =\frac{\sin {\theta}}{\cos {\theta}} \\[ 7pt ] &\quad 1 + \tan^{2}{\theta} =\frac { 1 }{ \cos^{2}{\theta}} \end{align*}ただし
\begin{align*} &\quad \sin^{2}{\theta} = \left(sin \theta \right)^{2} \\[ 7pt ] &\quad \cos^{2}{\theta} = \left(cos \theta \right)^{2} \\[ 7pt ] &\quad \tan^{2}{\theta} = \left(tan \theta \right)^{2} \end{align*}これらの相互関係は角の大きさに関わらず必ず成り立ちます。
角の大きさに関わらず必ず成り立つので、利用頻度が高い。絶対に覚えよう。
三角比の相互関係を導出しよう
三角比の相互関係を表す式を導出してみましょう。
既習内容を確認できたり、式変形のコツを知ることができたりします。ぜひともチャレンジして下さい。
正弦と余弦の相互関係を導出しよう
正弦と余弦の相互関係
\begin{align*} \quad \sin^{2}{\theta} + \cos^{2}{\theta} =1 \end{align*}座標平面において、中心を原点Oとする半径rの円と、その円周上の点P(x,y)を考えます。
点Pからx軸に垂線を下ろすと、OPを斜辺とする直角三角形ができます。この直角三角形において三平方の定理が成り立つので、以下の式を得ることができます。
ここから腕の見せ所になります。得られた等式を変形をしていきます。まず、両辺をr2で割ります。
正弦と余弦の相互関係の導出 2⃣
\begin{align*} &\vdots \\[ 7pt ] \quad x^{2} &+y^{2} = r^{2} \end{align*}両辺を $r^{2}$ で割ると
\begin{align*} \quad \frac{x^{2}}{r^{2}} +\frac{y^{2}}{r^{2}} = 1 \end{align*}次に、指数法則を利用して、左辺の各項を変形します。
正弦と余弦の相互関係の導出 3⃣
\begin{align*} &\vdots \\[ 7pt ] \quad \frac{x^{2}}{r^{2}} &+\frac{y^{2}}{r^{2}} = 1 \end{align*}指数法則より
\begin{align*} \quad \left(\frac{x}{r} \right)^{2} + \left(\frac{y}{r} \right)^{2} =1 \end{align*}左辺の各項を三角比に置き換えて整理します。
正弦と余弦の相互関係の導出 4⃣
\begin{align*} &\vdots \\[ 7pt ] \quad \left(\frac{x}{r} \right)^{2} &+ \left(\frac{y}{r} \right)^{2} =1 \end{align*}ここで
\begin{align*} &\quad \cos \theta = \frac{x}{r} \\[ 7pt ] &\quad \sin \theta = \frac{y}{r} \end{align*}より
\begin{align*} \quad \left(\cos \theta \right)^{2} + \left(\sin \theta \right)^{2} &=1 \\[ 7pt ] \quad \cos^{2}{\theta} + \sin^{2}{\theta} &=1 \\[ 7pt ] \therefore \ \sin^{2}{\theta} +\cos^{2}{\theta} &=1 \end{align*}正弦と余弦の相互関係を導出するために、三平方の定理、等式の性質、指数法則を利用しています。
指数法則を利用した変形は意外とできない人が多い。累乗を扱う機会が多いのでしっかりマスターしておこう。
正弦と余弦の相互関係の導出をまとめると以下のようになります。
要注意! sin2θとsinθ2は別物!?
定義に無頓着な人ほど、sin2θとsinθ2の扱いを一緒にします。
角θに対する正弦はsinθと表します。この正弦の値を2乗するとき、どのように表せば良いでしょうか?
三角比の累乗の表し方
正しい表し方 … $\left(\sin \theta \right)^{2}$ または $\sin^{2}{\theta}$
誤った表し方 … $\sin{\theta}^{2}$
角θに対する正弦はsinθと定義されているので、sinθを1つの記号として扱います。
ですから、角θに対する正弦sinθの2乗は、丁寧に表せば(sinθ)2となります。また、カッコを外して簡略化した表し方がsin2θです。
それに対して誤った表し方のsinθ2は、角θ2に対する正弦を表します。
たとえば、30°に対する正弦と(30°)2=900°に対する正弦は等しくなりません。このように、(sinθ)2とsinθ2は全くの別物です。
このような誤解が生じたのは、角θに指数が付いてしまうからです。これを防ぐため、三角比の累乗では、正弦や余弦の値を累乗していることが分かるようにsinやcosの直後に指数を書くようにします。
カッコの有無で式の意味が変わってしまうので、定義を正しく覚えよう。また、三角比の累乗を表す場合、これまでとは違う独特の表記なので早く慣れよう。
正弦・余弦・正接の相互関係を導出しよう
正弦・余弦・正接の相互関係
\begin{align*} \quad \tan{\theta} =\frac{\sin {\theta}}{\cos {\theta}} \end{align*}三角比の拡張で得られた3つの式を利用して導出します。まず、正弦と余弦の式を変形します。
正弦・余弦・正接の相互関係の導出 1⃣
\begin{align*} \quad \sin \theta = \frac{y}{r} \end{align*}より
\begin{align*} \quad y = r \sin \theta \end{align*}同様に
\begin{align*} \quad \cos \theta = \frac{x}{r} \end{align*}より
\begin{align*} \quad x = r \cos \theta \end{align*}変形した2式を正接の式に代入して整理します。
正弦・余弦・正接の相互関係の導出 2⃣
\begin{align*} &\vdots \\[ 7pt ] \quad y &= r \sin \theta \\[ 7pt ] &\vdots \\[ 7pt ] \quad x &= r \cos \theta \end{align*}これらを
\begin{align*} \quad \tan \theta = \frac{y}{x} \end{align*}に代入すると
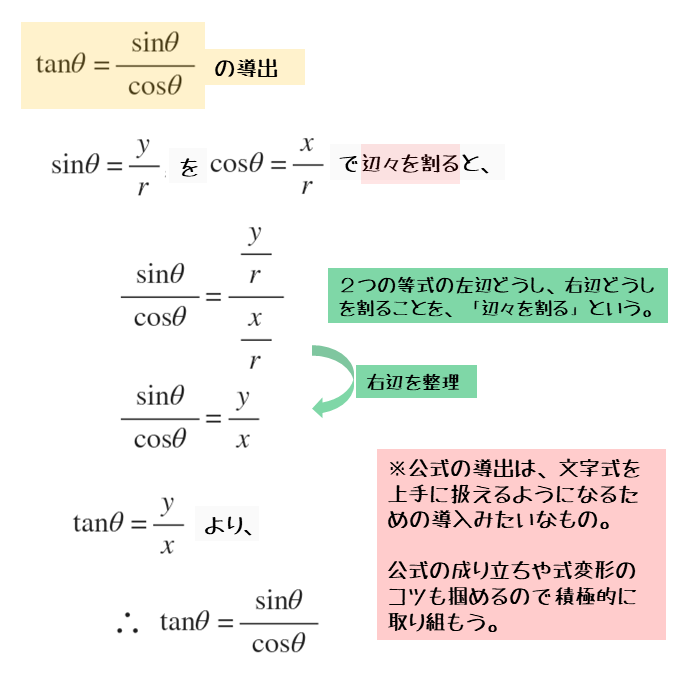
\begin{align*} \quad \tan \theta &= \frac{r \sin \theta}{r \cos \theta} \\[ 7pt ] \therefore \ \tan \theta &= \frac{\sin \theta}{\cos \theta} \end{align*}別の導出例は以下のようになります。「辺々割る」という耳慣れない用語がありますが、左辺どうし、右辺どうしを割るという意味です。
「辺々割る」とは、見た目は異なるが等しい値で両辺を割ること。等式の性質の応用的な使い方。等しい関係であれば、必ず同じ数や式で乗除算しなくても良いということ。等比数列の一般項を求めるときにもよく利用される。
余弦と正接の相互関係を導出しよう
余弦と正接の相互関係
余弦と正接の相互関係は、正弦と余弦の相互関係から導出されます。この相互関係は、等式の証明や微積の単元(特に数3)などでよくお世話になります。
正弦と余弦の相互関係を表す式を変形します。
余弦と正接の相互関係の導出 1⃣
両辺を $\cos^{2}{\theta}$ で割ると
\begin{align*} \quad \frac{\sin^{2}{\theta}}{\cos^{2}{\theta}} + 1 = \frac{1}{\cos^{2}{\theta}} \end{align*}指数法則より
\begin{align*} \quad \left( \frac{\sin \theta}{\cos \theta} \right)^{2} + 1 = \frac{1}{\cos^{2}{\theta}} \end{align*}次に、正弦・余弦・正接の相互関係を利用します。
余弦と正接の相互関係の導出 2⃣
ここで
\begin{align*} \quad \tan {\theta} =\frac{\sin {\theta}}{\cos {\theta}} \end{align*}より
\begin{align*} \quad \left( \tan \theta \right)^{2} + 1 &= \frac{1}{\cos^{2}{\theta}} \\[ 7pt ] \quad \tan^{2}{\theta} + 1 &= \frac{1}{\cos^{2}{\theta}} \\[ 7pt ] \quad \therefore \ 1 + \tan^{2}{\theta} &=\frac{1}{\cos^{2}{\theta}} \end{align*}指数法則を上手に利用して変形しています。また、累乗の表し方にも注意が必要です。
次は、三角比の相互関係を扱った問題を実際に解いてみましょう。