数学３
今回は、漸化式と極限について学習しましょう。
漸化式は数学Ｂ「数列」で学習します。特に、隣接２項間の漸化式は入試でも頻出なので、しっかりマスターしておきたいところです。
今回は極限の話がメインなので、隣接2項間の漸化式についての詳しい解説は後述します。忘れた人はご確認下さい。
漸化式と極限を扱った問題を解いてみよう
次の問題を考えてみましょう。
例題１
\begin{align*}
&\quad a_1 = 5 \ , \ a_{n+1} = \frac{2}{3} a_n + 1 \\[ 7pt ]
&\qquad (n = 1 \ , \ 2 \ , \ 3 \ , \cdots ) \\[ 7pt ]
&\text{で定義される数列 $\{ a_n \}$ について} \\[ 5pt ]
&\quad \displaystyle \lim_{ n \to \infty } a_n \\[ 7pt ]
&\text{を求めよ。}
\end{align*}
例題１の解答・解説
例題１は、数列｛ａn｝の一般項ａn の極限を求める問題です。極限を求めるためには、漸化式から数列｛ａn｝の一般項ａnを求める必要があります。
特性方程式を用いて漸化式を変形し、新しい数列の一般項から数列｛ａn｝の一般項ａnを求めます。
例題１の解答例 1⃣
\begin{align*}
&\text{漸化式を変形すると} \\[ 5pt ]
&\quad a_{n+1} – 3 = \frac{2}{3} \left( a_n – 3 \right) \\[ 7pt ]
&\text{数列 $\{ a_n – 3 \}$ は} \\[ 5pt ]
&\quad \text{初項} \ a_1-3 = 5-3 =2 \\[ 7pt ]
&\quad \text{公比} \ {\scriptsize {\frac{2}{3}}} \\[ 7pt ]
&\text{の等比数列であるので、その一般項は} \\[ 5pt ]
&\quad a_n – 3 = 2 \cdot {\left( \frac{2}{3} \right)}^{n-1} \\[ 7pt ]
&\text{よって、数列 $\{ a_n \}$ の一般項 $a_n$ は} \\[ 5pt ]
&\quad a_n = 2 \cdot {\left( \frac{2}{3} \right)}^{n-1} +3
\end{align*}
数列｛ａn｝の一般項ａnを求めたら、極限値を求めます。
例題１の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad a_n = 2 \cdot {\left( \frac{2}{3} \right)}^{n-1} +3 \\[ 7pt ]
&\text{よって}
\end{align*}
\begin{align*}
\quad &\displaystyle \lim_{ n \to \infty } a_n \\[ 7pt ]
= \ &\displaystyle \lim_{ n \to \infty } \biggl\{ 2 \cdot {\left( \frac{2}{3} \right)}^{n-1} +3 \biggr\} \\[ 7pt ]
= \ &3
\end{align*}
漸化式と極限の関係
例題１の結果から、一般項ａnの極限値について以下のことが分かります。
特性方程式の解と極限値との関係
\begin{align*}
&\text{特性方程式} \\[ 5pt ]
&\quad \alpha = \frac{2}{3} \alpha + 1 \\[ 7pt ]
&\text{の解は $\alpha = 3$ であり、また} \\[ 5pt ]
&\quad a_1 = 5 \ , \ a_{n+1} = \frac{2}{3} a_n + 1 \\[ 7pt ]
&\text{の $\displaystyle \lim_{ n \to \infty } a_n$ も} \\[ 5pt ]
&\quad a_n \to \alpha = 3 \\[ 7pt ]
&\text{となる。}
\end{align*}
以上のことから、漸化式ａn+1＝ｐａn＋ｑ（ｐ，ｑは定数，ｐ≠１）で表される数列｛ａn｝では、その一般項ａnの極限値は特性方程式の解αの値に近づくことが分かります。
このことを知っていると、極限値を予測したうえで問題に取り組むことが可能になります。
極限値を視覚的に見て予測する
次は一般項ａnの極限値を視覚的に捉えてみましょう。特性方程式のαをｘに置き換えてみます。
特性方程式のαをｘに置き換える
\begin{align*}
&\text{特性方程式の $\alpha$ を $x$ に置き換えると} \\[ 5pt ]
&\quad x = \frac{2}{3} x + 1
\end{align*}
特性方程式がｘについての方程式になりました。この式は以下のように解釈することができます。
グラフの交点の話に置き換える
\begin{align*}
&\quad x = \frac{2}{3} x + 1 \\[ 7pt ]
&\text{は、$2$ つのグラフ} \\[ 5pt ]
&\left\{
\begin{array}{l}
y = x \\
y = \frac{2}{3} x + 1
\end{array}
\right. \\[ 10pt ]
&\text{の交点の $x$ 座標を求める式である。}
\end{align*}
以上のことから、特性方程式の代わりにグラフの交点の話に置き換えると、漸化式の変形を以下のように解釈できます。
漸化式をグラフを利用して変形
\begin{align*}
&\text{$1$ 次型の漸化式 } \\[ 5pt ]
&\quad a_{n+1} = pa_{n} + q \\[ 7pt ]
&\qquad ( p \ , \ q \ \text{は定数} \ , \ p \neq 1 ) \\[ 7pt ]
&\text{は、$2$ つのグラフ} \\[ 5pt ]
&\left\{
\begin{array}{l}
y = x \\
y = px + q
\end{array}
\right. \\[ 10pt ]
&\text{の交点の $x$ 座標を $x = \alpha$ とすると} \\[ 5pt ]
&\quad a_{n+1} = pa_{n} + q \\[ 7pt ]
&\qquad \iff a_{n+1} – \alpha = p \left( a_{n} – \alpha \right) \\[ 7pt ]
&\text{と変形できる。}
\end{align*}
さらに先ほどの極限値の話も加えると、漸化式と極限の関係をグラフを使って以下のように解釈できます。
極限とグラフの関係
\begin{align*}
&\text{$1$ 次型の漸化式 } \\[ 5pt ]
&\quad a_{n+1} = pa_{n} + q \\[ 7pt ]
&\qquad ( p \ , \ q \ \text{は定数} \ , \ p \neq 1 ) \\[ 7pt ]
&\text{の $\displaystyle \lim_{ n \to \infty } a_n$ は、$2$ つのグラフ} \\[ 5pt ]
&\left\{
\begin{array}{l}
y = x \\
y = px + q
\end{array}
\right. \\[ 10pt ]
&\text{の交点の $x$ 座標を $x = \alpha$ とすると} \\[ 5pt ]
&\text{$\displaystyle \lim_{ n \to \infty } a_n$ は} \\[ 5pt ]
&\quad a_n \to \text{交点の $x$ 座標 $\alpha$} \\[ 7pt ]
&\text{となる。}
\end{align*}
このことから、一般項ａnは、ｎ→∞のとき、２つのグラフの交点のｘ座標に近づくことが分かります。
このように漸化式をグラフと関連付けることは、極限値が視覚的に見える（予測できる）というメリットがあります。
高校数学では抽象的な数式を扱うことが多いので、イメージの湧かない人が多いかもしれません。ですから、グラフで視覚化できると、問題に取り組みやすくなるのではないかと思います。
次は、いくつかの例をグラフを使って考えてみましょう。
極限値を予測してみよう
例題２
\begin{align*}
&\quad a_1 = 1 \ , \ a_{n+1} = \sqrt{ 2a_n + 3 } \\[ 7pt ]
&\qquad (n = 1 \ , \ 2 \ , \ 3 \ , \cdots )
\end{align*}
で定義される数列 $\{ a_n \}$ について、数列 $\{a_n\}$ が極限値 $\alpha$ をもつとき、$\alpha$ の値を求めよ。
扱いの難しそうな漸化式ですが、グラフを使えば極限値を予測することができます。
極限値をグラフで予測する
\begin{align*}
&\text{漸化式より、$2$ つのグラフ} \\[ 5pt ]
&\left\{
\begin{array}{l}
y = x \\
y = \sqrt{ 2x + 3 }
\end{array}
\right. \\[ 10pt ]
&\text{の交点の $x$ 座標を考える。}
\end{align*}
２つのグラフを図示すると以下のようになります。
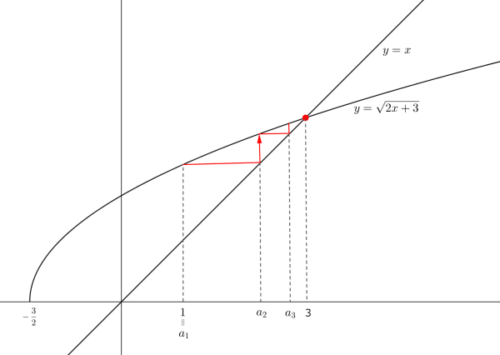交点のｘ座標が極限値 図からｎ→∞のとき、ａnは２つのグラフの交点のｘ座標３に近づくことが予想されます。これより、$\displaystyle \lim_{ n \to \infty } a_n = 3$ と予測できます。
グラフを用いずに極限値を予測するとすれば以下のようにします。
例題２の解答例
\begin{align*}
&\displaystyle \lim_{ n \to \infty } a_n = \alpha \ \text{とすると} \\[ 5pt ]
&\quad \displaystyle \lim_{ n \to \infty } a_n = \displaystyle \lim_{ n \to \infty } a_{n+1} = \alpha \\[ 7pt ]
&\text{より、漸化式から} \\[ 5pt ]
&\quad \alpha = \sqrt{2 \alpha +3} \quad \cdots \text{①} \\[ 7pt ]
&\text{①の両辺を $2$ 乗すると} \\[ 5pt ]
&\quad {\alpha}^{2} = 2 \alpha +3 \\[ 7pt ]
&\text{これを解くと} \\[ 5pt ]
&\quad \alpha = -1 \ , \ 3 \\[ 7pt ]
&\text{$\alpha = -1$ は①を満たさないので} \\[ 5pt ]
&\quad \alpha = 3
\end{align*}
一般項ａnの極限値が３であると予測したうえで答案を作成します。実際の記述では、一般項ａnを求めてから、ｎ→∞のときの極限値を求めます。
次の問題でも極限値を予測してみましょう。
例題３
\begin{align*}
&\quad a_1 = 3 \ , \ a_{n+1} = \frac{1}{2} \left( a_n + \frac{1}{a_n} \right) \\[ 7pt ]
&\qquad (n = 1 \ , \ 2 \ , \ 3 \ , \cdots )
\end{align*}
で定義される数列 $\{ a_n \}$ について、数列 $\{a_n\}$ が極限値 $\alpha$ をもつとき、$\alpha$ の値を求めよ。
こちらも一見して扱いにくそうな漸化式です。こんな漸化式でもグラフを使えば極限値を予測できます。
極限値をグラフで予測する
\begin{align*}
&\text{漸化式より、$2$ つのグラフ} \\[ 5pt ]
&\left\{
\begin{array}{l}
y = x \\
y = \frac{1}{2} \left( x + \frac{1}{x} \right)
\end{array}
\right. \\[ 10pt ]
&\text{の交点の $x$ 座標を考える。なお} \\[ 5pt ]
&\quad {\scriptsize {y = \frac{1}{2} \left( x + \frac{1}{x} \right)}} \\[ 7pt ]
&\text{のグラフは} \\[ 5pt ]
&\quad y=\frac{1}{2} x \ , \ y= \frac{1}{2x} \\[ 7pt ]
&\text{のグラフを足し合わせて図示する。}
\end{align*}
２つのグラフを図示すると以下のようになります。
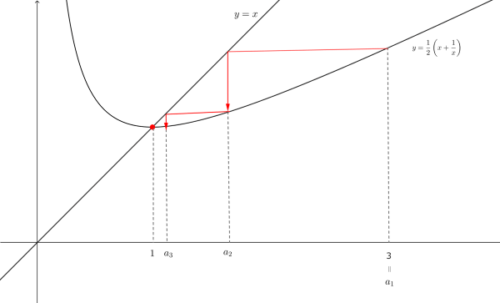交点のｘ座標が極限値 図からｎ→∞のとき、ａnは２つのグラフの交点のｘ座標１に近づくことが予想されます。これより、$\displaystyle \lim_{ n \to \infty } a_n = 1$ と予測できます。
例題のような隣接２項間の漸化式であれば、グラフを用いて極限値を予測できます。極限値を予測したうえで問題に取り組めるので、ほとんどの場合で答案を手際よく作成できるようになります。
ただし、実際には漸化式から一般項を求めたり、証明が必要だったりするので、あくまでも予測として利用しましょう。
例題２，３は誘導型の小問形式で出題
例題２，３のような問題は、一般に誘導型の問題になっています。たとえば例題３は、以下のような小問形式で出題されます。
例題２，３は実際は小問形式
\begin{align*}
&\quad a_1 = 3 \ , \ a_{n+1} = \frac{1}{2} \left( a_n + \frac{1}{a_n} \right) \\[ 7pt ]
&\qquad (n = 1 \ , \ 2 \ , \ 3 \ , \cdots ) \\[ 7pt ]
&\text{で定義される数列 $\{ a_n \}$ について} \\[ 5pt ]
&(1) \ \text{数列 $\{a_n\}$ が極限値 $\alpha$ をもつとき、$\alpha$ の値を求めよ。} \\[ 7pt ]
&(2) \ (1) \ \text{の $\alpha$ について、$a_n \geqq 1 \ , \ a_{n+1} -1 \leqq \frac{1}{2} \left( a_{n} -1 \right)$ を示せ。} \\[ 7pt ]
&(3) \ \displaystyle \lim_{ n \to \infty } a_n = \alpha \ \text{であることを示せ。}
\end{align*}
小問(2)，(3)はグラフを見れば明らかですが、きちんと証明する必要があります。
また、小問をひとまとめにして出題される場合もあります。そのような場合でも、小問形式の問題をしっかりマスターしておけばきちんと対応できるでしょう。
次ページでは隣接２項間の漸化式について解説しています。数学Ｂの数列では頻出なので、少しでも足しになれば幸いです。
