数と式|絶対値について

今回は、絶対値について学習しましょう。中学でも学習しますが、意外と理解に苦しむ人が多いのが絶対値です。
高校数学ではもう少し詳しく学習するので、絶対値の定義やその意味をしっかりと理解しましょう。
絶対値のおさらい
絶対値は、実数aを数直線上で表したときの原点Oからaまでの距離のことです。たとえば、-3の絶対値は3です。「絶対値」という用語は、中学では正負の数の単元で登場します。
正負の数は、向きと絶対値の2つの意味をもつ数です。正負の数は向きをもつので、そのまま絶対値に用いると問題が起きます。そうは言っても、正負の数には大きさ(絶対値)の情報も含まれるので、全く使わないのは勿体ないです。
そういうわけで、正負の数から絶対値の情報だけを使いたいときは特別な記号を使います。その記号が正負の数に付いていれば、絶対値だけを考えていることが分かります。
絶対値を記号化して扱うのが新たに学習することの1つです。
絶対値の記号化
高校数学での絶対値の定義は以下のようになります。
絶対値の定義
絶対値とは、実数aを数直線上で表したときの原点Oからaまでの距離を言い、このときaの絶対値という。またaの絶対値を|a|と表す。
絶対値を記号化して使えるようになるのがここでの目標です。
数はもちろん、整式であっても縦線2本で挟めば絶対値になります。この記号を使えば「この数式は点と原点との距離を考えています」とアピールできます。
絶対値の記号を実際に使ってみよう
数の絶対値
ある数の絶対値、たとえば3の絶対値|3|と-3の絶対値|-3|について考えてみましょう。
3の絶対値|3|は、3に対応する点Aと原点Oとの距離OAを表します。また、-3の絶対値|-3|は、-3に対応する点Bと原点Oとの距離OBを表しています。
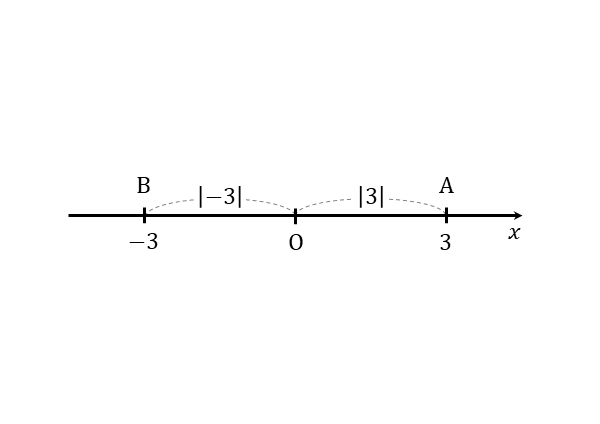
図から分かるように、3,-3の絶対値は、距離を測る向きが異なるだけでともに3であることが分かります。このように符号が向きを表すので、正負の数のままでは絶対値を表せないことが分かると思います。
また、絶対値が0でないとき、絶対値の等しい点が必ず2つあることも分かります。
未知の数の絶対値
未知の数a,-aの絶対値を記号化した|a|,|-a|を考えます。ただし、aを正の数(a>0)と考えています。
aの絶対値|a|は、aに対応する点Aと原点Oとの距離OAを表します。また、-aの絶対値|-a|は、-aに対応する点Bと原点Oとの距離OBを表します。
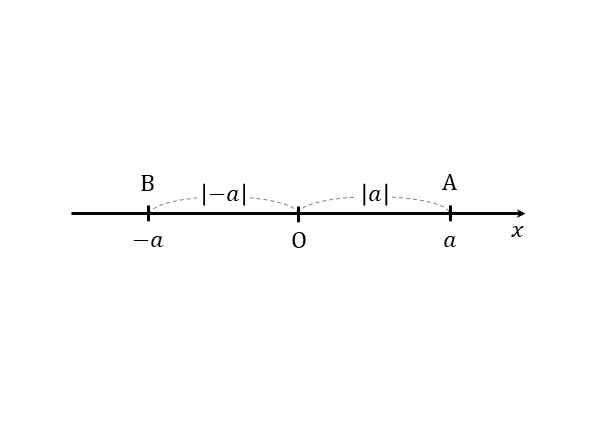
数のときと同じように、縦線2本で未知の数a,-aを挟めば絶対値を表すことができます。文字を使うと分かりにくくなりますが、絶対値の記号で挟まれていれば正の数と同じ扱いをします。
絶対値を記号なしで表す
数の絶対値の場合で規則性を知る
正負の数は向きと絶対値の2つの情報をもちます。それに対して、絶対値は距離(大きさ)の情報1つだけなので、絶対値の記号は便利な記号です。ただ、絶対値を計算に利用するとき、この記号が邪魔になります。
ですから、絶対値の記号の外し方を知っておく必要があります。ただし、記号を外した後でも絶対値を扱っていることは忘れないようにしましょう。
絶対値の計算は、距離(大きさ)を扱った計算なので、正の数だけの計算と考えるとよい。向きの情報を含む正負の数の計算とは異なることに注意しよう。
先ほど例に挙げた3の絶対値|3|と-3の絶対値|-3|を記号なしで表すと、ともに3になります。
±3の絶対値
数直線から
\begin{align*} &\quad \left|3 \right|=3 \\[ 7pt ] &\quad \left|-3 \right|=3 \end{align*}3や-3のように具体的な値が分かっていれば、絶対値の記号を簡単に外せます。それに対して、文字を含む場合、具体的な値が分からないので、絶対値の記号を上手く外せません。
数や文字に関わらず、絶対値の記号を外せる方法を知っておく必要があります。
正の数の場合、その絶対値は記号を外しても正の数と見た目は同じです。このことを利用します。
正の数の絶対値
$3$ は正の数であり、その絶対値は
\begin{align*} \quad \left|3 \right|=3 \end{align*}正の数を絶対値としてそのまま利用できる。
正の数であれば、記号がなくても絶対値としてそのまま流用できる。
負の数の絶対値では正の数にする処理を
問題なのは負の数の場合です。負の数-3の絶対値|-3|は、記号なしで表せば3になります。
この場合、絶対値の記号をそのまま外すと-3になってしまいます。負の数のままでは絶対値の定義に反するので、記号を外すだけでは上手くいきません。
負の数の絶対値を、絶対値の定義に反することなく、かつ記号を外して表すためには、マイナスの符号が邪魔になります。
このマイナスの符号を適切に処理するのが、負の数の絶対値を扱うときのポイントになります。
負の数の絶対値
$-3$ は負の数であり、その絶対値は
\begin{align*} \quad \left|-3 \right|=\underline{-\left(-3 \right)}=3 \end{align*}負の数の絶対値では、符号の処理を忘れないこと。
負の数の絶対値では、絶対値の記号を外すには下線部のような処理を施しています。マイナスの符号をどのようにして処理するのかを知っておくことが大切です。
負の数と正の数では、向きが異なります。負の数を正の数と同じ向きにできれば、正の数と同じ扱いができます。そのために負の数に-1を掛けて(カッコの前にマイナスをつけて)正の数に変えています。
負の数から正の数に変えるには、-1を掛ければよい。-1を掛ける処理は、数の値を変えることなく、符号だけを変える処理。
絶対値の記号の外し方についてまとめると以下のようになります。
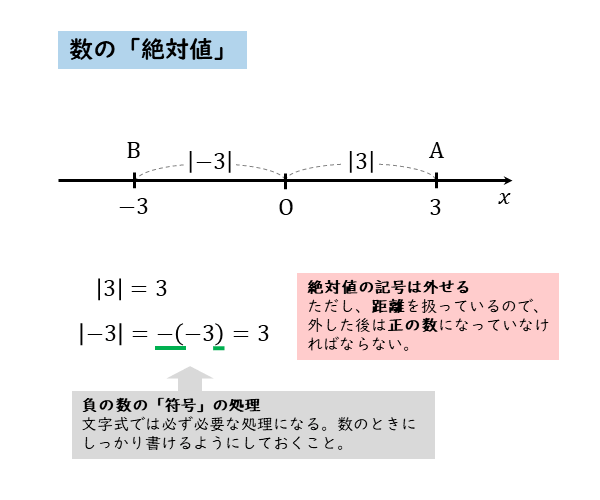
負の数の絶対値では「負の数を正の数にする処理を行う」と覚えよう。「符号を取る」では単項式や多項式などの整式に対応できない。
未知の数で絶対値の記号を外す
数の絶対値であれば、数の符号をみればその正負を判断でき、絶対値の記号を簡単に外せます。
しかし、未知の数aの場合、外見から正負を判断することができないので、迂闊に記号を外せません。
正負を判断できさえすれば、未知の数aであっても絶対値の記号を外せます。そのための手段が「場合分け」です。
未知の数aの値は「正の数のとき」「0のとき」「負の数のとき」の3通りが考えられます。ただし、未知の数aが0のとき、絶対値の記号を外す前後に違いがないので、正の数のときに含めます。
未知の数aの絶対値
\begin{align*} [ \ 1 \ ] \ a \geqq 0 \ \text{のとき} \end{align*}$a$ は $0$ または正の数なので
\begin{align*} \quad \left|a \right|=a \end{align*}$0$ 以上の数であれば、そのまま利用できる。
\begin{align*} [ \ 2 \ ] \ a \lt 0 \ \text{のとき} \end{align*}$a$ は負の数なので
\begin{align*} \quad \left|a \right|=-a \end{align*}負の数であれば、符号の処理が必要。
\begin{align*} &[ \ 1 \ ] \ , \ [ \ 2 \ ] \ \text{より} \\[ 5pt ] &\quad |a| = \begin{cases} a & ( a \geqq 0 ) \\ -a & ( a \lt 0 ) \end{cases} \end{align*}未知の数aに対する場合分けは、「0以上のとき」と「負の数のとき」の2通りです。
未知の数aが負の数であれば、絶対値の記号をそのまま外すわけにはいきません。ですから、未知の数aに-1を掛けて、負の数が正の数になるような処理を行います。
-1を掛けたことで外見上は負の数に見えても、aが負の数なので-aは正の数。未知の数aに負の数を代入してみよう。
具体的な正負の数で記号の外し方の規則性を見つけ、未知の数aに対しても同じ扱いをしています。
未知の数の絶対値の扱いについてまとめると以下のようになります。
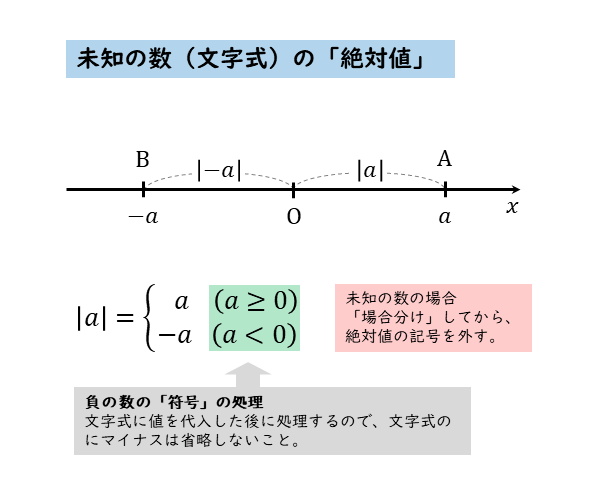
具体例から一般化(公式化)することのメリットは、条件に合致すれば同じように扱うことができる点にあります。
易しく具体的な数を扱っているときに過程を意識して学習することが大切です。そうすれば、文字を扱った抽象的な整式になっても理解できるようになります。
Recommended books
オススメその1
予習の際に理解が進めば授業のスピードについていくことができ、復習や課題をこなす時間も少なくて済みます。予習や復習の補助教材に向いている教材が『とってもやさしい数学』シリーズです。
とってもやさしい数学1・Aでは2冊とも中学で学習した内容にも触れており、中学内容と高校内容とのつながりを把握しやすい教材です。
一学期のうちは不安を抱えながら学習を進めていく人も多いかと思います。スタートで躓かないためにも易しく取り組みやすい教材を使うのも一つのやり方です。無理をして内容の難しい教材を使うよりもはるかに良いでしょう。
基礎的な内容を扱っているので、数学が苦手な人でも取り組みやすくなっています。興味のある人はぜひ一読してみて下さい。
『高校とってもやさしい数学1・A 改訂版 その1』は「数と式」「2次関数」の単元を扱っています。
『高校とってもやさしい数学1・A 改訂版 その2』は「場合の数」「確率」「整数の性質」「図形の性質」「三角比」の単元を扱っています。
オススメその2
『高校の数学I・Aが1冊でしっかりわかる本』は、これ1冊で数学1・Aの全範囲を復習できます。内容のレベルは「とってもやさしい」シリーズとそれほど変わらず、教科書レベルです。
本書と「とってもやさしい」シリーズのページ数を比較してみました。「とってもやさしい」シリーズは、1冊ごとのページ数が少ないのですが、分冊なのが難点です。
- 高校とってもやさしい数学1・A 改訂版 その1:175ページ
- 高校とってもやさしい数学1・A 改訂版 その2:189ページ
- 高校の数学I・Aが1冊でしっかりわかる本:192ページ
ページ数を比べると分かるように、本書の方が1冊でも遥かにページ数が少ないので、短時間でこなすことができます。
紹介した教材を使うとした場合、高校1年生であれば「とってもやさしい」シリーズで復習し、高校2,3年生であれば『高校の数学I・Aが1冊でしっかりわかる本』と「とってもやさしい」シリーズを組み合わせて復習すると良いでしょう。
こんな人に向いています
- 定期試験や大学受験のための基礎を固めて、成績を上げたい高校生へ。
- 医療看護系入試、高卒認定試験などの対策で、短期間で数学1・Aを理解したい方へ。
- 学び直しや頭の体操をしたい大人の方へ。
さいごに、もう一度まとめ
- 絶対値は、ある点と原点との距離のことで正の数になる。
- 絶対値は記号を使って表せる。
- 正の数の絶対値では、記号を外して絶対値として扱える。
- 負の数の絶対値では、記号を外すときは負の数を正の数にする。
- 未知の数の絶対値では、場合分けをしてから記号を外す。
















