物理のヒント集|ヒントその3.v-tグラフでの面積と変位の関係

第3回の物理のヒント集は、v-tグラフにおける面積と変位との関係についてです。v-tグラフを上手に利用できると、等速直線運動や等加速度直線運動を扱った問題に苦労せずに済みます。
v-tグラフにおける面積と変位の関係

メガネ先生っ! v-tグラフで求めた面積が、なぜ距離や変位に等しくなるのでしょうか? そもそも、面積が距離に等しくなることがあるのでしょうか?

面積ではなくて、符号付きの面積じゃよ。この話は数学でのイメージが強いせいか、違和感をもつ生徒が意外と多いんじゃ。

そうなんですかっ! 僕だけじゃないようなので、少し安心しましたっ!

数学では面積を求めるとき、単位のない場合が多いせいかもしれんのぅ。それでも注意深くグラフを観察する習慣を付けてほしいがの。
数量の表す物理量が同じ
2人の会話にあったように、直線運動の単元で「v-tグラフにおける図形の面積は、距離または変位に等しい」と学習します。
「面積と距離が等しい」というのは、幾何学的(図形的)に考えるとおかしな感じがします。なぜなら、面積の単位は m2 や cm2 であるのに対して、距離の単位は m や cm であるからです。
「単位の次元が合っていない!」と思うはずです。実はそれはただの思い込みや習慣に過ぎません。
縦軸と横軸の両方が長さの次元を持っているのは、数学の中だけの話です。数学では、縦軸と横軸の1目盛りが 1cm や 1m と仮定されています。最初のうちは問題文に但し書きがあったのですが、途中から記載されなくなります。
もしかすると、自分たちもそのことに次第に慣れてしまったせいか、縦軸や横軸の次元は長さだと勝手に思い込んでしまったのかもしれません。
v-tグラフにおいて、面積と距離(変位)が等しいとは、面積が表す物理量と、距離(または変位)が表す物理量とが同じという意味を表しています。
このように物理量に注目すると、特定の物理量を、あるグラフでは面積として扱ったり、別のグラフでは距離として扱ったりすることができるようになります。そのおかげで、v-tグラフでは、面積を距離または変位として扱うことができるわけです。
物理では、縦軸と横軸の単位が長さとは限らない。軸の次元に注意しよう。
軸の次元に注意しよう
物理において、グラフを扱うときにまずすべきことは、軸の次元を確認することです。
v-tグラフでは、縦軸がv軸であるので、次元は [m/s] つまり [長さ/時間] です。また、横軸はt軸であるので、次元は [t] つまり [時間] です。
このように縦軸と横軸の次元が設定されているとき、図形の面積の次元は、[長さ/時間] と [時間] の掛け算をすることになるので、[長さ] となります。また、距離や変位の次元も [長さ] です。
以上のことから、面積と距離(変位)が等しいというのは、図形的に等しいと言っているわけではなく、ともに長さの次元をもつ物理量として等しいという意味で言っていることが分かります。
軸の次元によって、面積のもつ次元が変わるので注意しよう。
符号付きの面積
v-tグラフでは、正負をもつ符号付きの面積は、距離ではなく、変位を表します。
面積と言えば、数学では必ず正の値になります。これは面積の大きさ、つまりスカラー量を求めているからです。それに対して、物理では一般にベクトル量を扱うので、値の正負には意味があります。
長さの次元をもつ値に正負がある場合、それは距離ではなく変位です。正の変位であれば、初めの位置(基準)から正の向きに、どれだけ移動したのか (2点間の距離) を表します。
また、負の変位であれば、初めの位置(基準)から負の向きに、どれだけ移動したのか(2点間の距離)を表します。
同じように、物理では面積にも正負があります。
たとえば、1つの軸だけの一次元の場合、v-tグラフにおける符号付きの面積は、以下のように定積分で定義されます。ただし、初めの時刻をt1 、終わりの時刻をt2 とします。
定積分で定義される面積
定積分で定義される面積は、グラフとt軸とに挟まれた部分の面積になります。この面積を定積分によって求めると、x(t2)-x(t1)が得られます。
定積分すると得られるのは変位
右辺のx(t2)-x(t1)は変位を表します。このことから「v-tグラフにおける符号付きの面積は変位に等しい」と言われるわけです。
さらに、符号付きの面積と変位の関係から、以下のようなことが分かります。
符号付きの面積と変位の関係
- 「 $v-t$ グラフでの符号付きの面積が正の値」
- ⇔ $x(t_2) – x(t_1) \gt 0$ より $x(t_1) \lt x(t_2)$
- ⇔「正の向きに変位した」
- 「 $v-t$ グラフでの符号付きの面積が負の値」
- ⇔ $x(t_2) – x(t_1) \lt 0$ より $x(t_1) \gt x(t_2)$
- ⇔「負の向きに変位した」
以上のことから、物体の運動を正しく解釈するには、得られる数の符号を大事にしなければいけないことが分かります。
次は実際にv-tグラフにおける面積を求めてみましょう。
面積を求めてみよう

なぜ、v-tグラフでの面積が距離(または変位)に等しくなるか分かったかの?

はいっ! 面積のもつ次元が長さになるので、物理量として等しいという意味だったのですねっ!

その通りじゃ。これでv-tグラフの使い道がさらに増えたわけじゃ。

そうですねっ! グラフの傾きだけでなく、面積も運動の様子を理解するのに役立つことが分かりましたっ!

ところで、定積分をまだ習っていないので、面積の求め方が分かりません。どのようにすれば良いのでしょうか?

定積分は数学2の範囲じゃから知らないのも当然じゃろう。では、具体例を使って求めてみようかの。
等速直線運動を表すv-tグラフにおける面積
図1のv-tグラフは等速直線運動を表します。ただし、0~8秒の間と8~10秒の間では速度が異なるので、2つの等速直線運動を行っています。
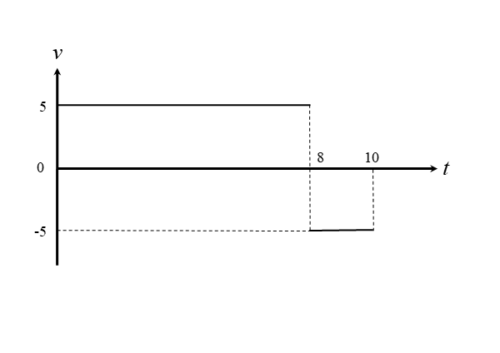
v-tグラフにおける面積とは、グラフとt軸とに挟まれた部分の面積のことです。0~8秒の間での面積は縦5、横8の長方形の面積で、8~10秒の間での面積は縦 5、横 2 の長方形の面積です。
このようにグラフとt軸とに挟まれた図形が長方形や台形などであれば、図形の公式を使って面積を求めることができます。ただ、このまま面積を求めてしまうと、その値は面積の大きさになるので注意が必要です。
面積の大きさは、時間内で進んだ距離を表します。距離を求める場合はこれで構いませんが、変位であれば符号付きの面積を求めなければなりません。
変位の正負はグラフがt軸の上側にあるのか下側にあるのかで分かります。
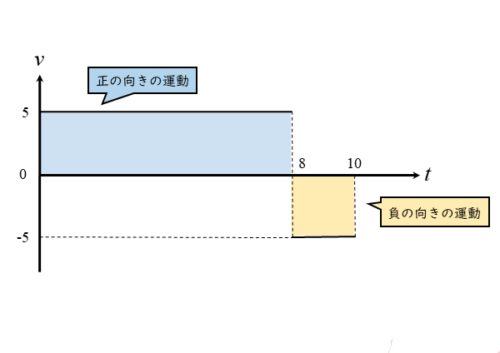
- グラフがt軸の上側 ⇔ 正の向きの運動 ⇔ 正の変位
- グラフがt軸の下側 ⇔ 負の向きの運動 ⇔ 負の変位
0 ~ 8 秒の間ではグラフがt軸の上側にあります。正の向きに運動することが分かるので、正の変位です。このことから、以下のようにして変位を求めることができます。
$0 \leqq t \leqq 8$ での変位
それに対して、8 ~ 10 秒の間ではグラフがt軸の下側にあります。負の向きに運動することが分かるので、負の変位です。このことから、以下のようにして変位を求めることができます。
$8 \leqq t \leqq 10$ での変位
面積の式の前に符号をつけておけば変位になります。また、0 ~ 10 秒の間での変位は以下のようになります。
$0 \leqq t \leqq 10$ での変位
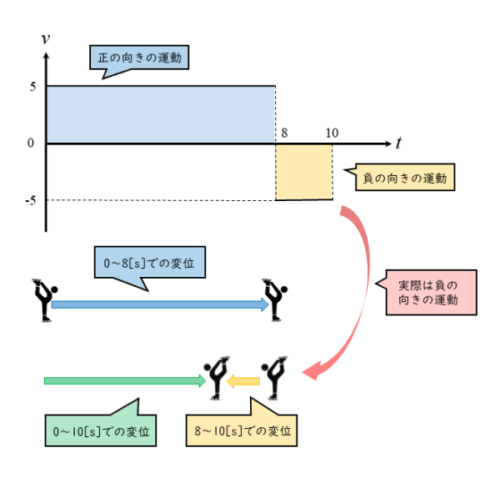
また、グラフから運動の様子をイメージする習慣を付けておきましょう。運動の様子をイメージできれば、どこを基準とした変位かも間違えずに済みます。
さいごにもう一度

どうだったかの? 定積分を知らなくても面積を求めることができるんじゃ。

図形が長方形や台形などであれば、公式を使って面積を求めることができますねっ! 簡単そうで安心しましたっ!

計算は簡単じゃが、物理では値の正負に意識を向けないとかなり苦労するぞい。扱っているのはベクトル量じゃからの。

値の正負に注意することが大切なんですね。意識しながら演習しますっ!
物理・物理基礎のオススメ本
- 宇宙一わかりやすい高校物理(力学・波動)
- 宇宙一わかりやすい高校物理(電磁気・熱・原子)
物理入門者や、物理を苦手にしている人に導入書としておすすめです。教科書が学習の中心であるべきですが、どうしても教科書で理解できない箇所が出てきたら本書で補完すると良いでしょう。イラストが豊富なので独学でも使えます。
分冊になっているので、力学と波動以外の分野はもう1冊の方になります。
- 秘伝の物理講義[力学・波動]
- 秘伝の物理講義[電磁気・熱・原子]
YouTubeで完全公開されている講義を再現したのが本冊です。また、別冊の「動画テキスト兼ポイント集」で物理の「わからない」を解決できます。公開模試、学校平均点全国No.1を取らせた実力派教師の講義は一読の価値あり。独学にも向き、標準以上も対応可能です。
分冊になっているので、力学と波動以外の分野はもう1冊の方になります。
物理教室(河合塾series)
所有していますが、これ1冊で基礎から応用まで十分対応できます。理系志望者は一読してほしいのが本書です。
物理の内容が分野ごとに章立てされており、各分野ごとに筋道を通した理解ができます。網羅性が高いのは当然ですが、「物理的な見方や考え方」が自然に身につくように丁寧に解説されています。
また、入試を意識して問題を多く扱っているのも特徴で、問題集代わりにも使えます。基礎を身に着けたい人は参考書として、応用力を養いたい人は問題集として、実力に応じて使いこなせる構成になっています。
問題集の『物理のエッセンス』は有名ですが、同じ河合塾seriesなので相性も良いです。
















