物理のヒント集|ヒントその5.フックの法則でマイナスの符号は必要か

第5回の物理のヒント集は、フックの法則についてです。フックの法則は、ばねの弾性力を求めるときに利用します。
フックの法則の右辺にマイナスの符号があるのはなぜ!?

メガネ先生っ!教えてくださいっ!

メガネ君はいつも元気じゃのぅ。

教科書や参考書によって、フックの法則の右辺にマイナスの符号があるときとないときがあります。

確かにあるのぅ。

x だけ伸びたり縮んだりしたとき、kx で弾性力の大きさが分かるので、マイナスの符号はいらないと思うのですが。

文字の定義に違いがあるんじゃよ。ただ公式を暗記すれば良いというわけではないんじゃ。

何ですとっ!

まだまだじゃのぅ。
フックの法則は視点の違いで2通りの表し方があります。教科書や参考書などによって表し方がまちまちですが、定義を確認すれば違いが分かります。
フックの法則の定義
ばねを引き伸ばす(押し縮める)と、ばねは自然長まで縮もう(伸びよう)とします。このとき、ばねに取り付けてある物体に力を及ぼします。この力のことを弾性力と言います。
ばねの伸び(縮み)を x とし、そのときの弾性力の大きさを F とします。このとき、F は x に比例し、F と x の間には次の関係式が成り立ちます。これをフックの法則と言います。
フックの法則
ただし
$F$:ばねの弾性力の大きさ $\mathrm{[ N ]}$
$k$:ばね定数 $\mathrm{[ N/m ]}$
$x$:ばねの伸びまたは縮み $\mathrm{[ m ]}$
弾性力の大きさとあるように、大きさだけのスカラー量を扱っています。もちろん、ばねの伸びや縮みも長さのことなのでスカラー量です。
つまり、右辺にマイナスの符号が付いていないフックの法則では、スカラー量としての等式になります。中学でも学習した弾性力やばねの伸びなどは、単に大きさだけに注目していたわけです。
中学では、大きさだけに注目していた。
それに対して高校では、ばねの弾性力や伸び(縮み)をベクトル量として扱います。一般に、以下のように表されます。
フックの法則(右辺にマイナスの符号あり)
ただし
$F$:ばねの弾性力 $\mathrm{[ N ]}$
$k$:ばね定数 $\mathrm{[ N/m ]}$
$x$:ばねの変位 $\mathrm{[ m ]}$
この式は、自然長からの伸びを表す変位と、ばね(物体)に作用している弾性力との間に成り立つ等式です。文字の定義が変わっていることに注意しましょう。
自然長からの伸びを表す変位と、ばねに作用している弾性力は、ともに大きさと向きをもつ一次元のベクトル量なので、この式はベクトル量としての等式になります。
高校では、大きさだけでなく、向きも考慮に入れて計算する。
ばねの弾性力をベクトル量として扱うと言っても、力にマイナスの符号が付くのは違和感を感じるかもしれません。
違和感を感じるのは、ばねが伸びたり縮んだりするときに弾性力がどのように働くのかをイメージできていないからです。
物理現象を理解した上で公式を覚えないと、様々な物理現象を扱った問題を解くことはできません。そうならないように、図解しながら学習することを心掛けましょう。
ばねが縮んだとき
水平方向にばねを伸び縮みさせるときを考えてみましょう。このとき、右向きを正の向きとし、右向きをプラス(+)、水平方向左向きをマイナス(-)で表します。また、ばね定数を k とします。
下図において、(a)はばねが自然長のときで、(b)はばねが自然長から長さ a だけ縮んだときを表しています。
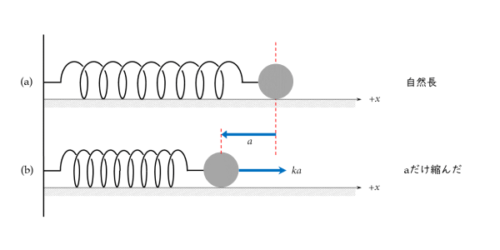
(b)のように、ばねが自然長から左向きにaだけ縮んだとき、ばねの変位を表すベクトルは-aとなります。
また、ばねの右端(または右端に取り付けた物体)は、自然長に戻ろうとして右向きに大きさkaの弾性力を受けます。この弾性力を表すベクトルは+kaです。
このことから、自然長からxだけ変位したとき、ばねの右端(または右端に取り付けた物体)の受ける弾性力を、向きを考慮してF(x)とおくと、(b)の場合は以下のような式が成り立ちます。
(b)の場合の弾性力
F(x)とおいたのは、変位の向きと弾性力の向きとの関係が分かるようにするためです。
(b)の場合、変位の向きが負の向きであるのに対して、弾性力の向きは正の向きであることが分かります。
ばねが伸びたとき
ばねが自然長から右向きに長さbだけ伸びるときも同様です。
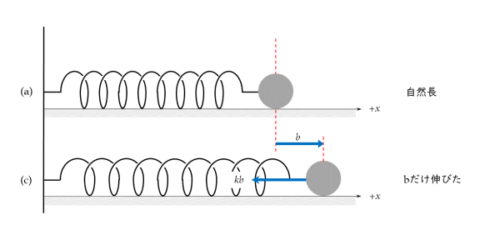
(c)のように、ばねが自然長から右向きにbだけ伸びたとき、ばねの変位を表すベクトルは+bとなります。
また、ばねの右端(または右端に取り付けた物体)は、自然長に戻ろうとして左向きに大きさ kb の弾性力を受けます。この弾性力を表すベクトルは-kbです。
このことから、(c)の場合、F(x)について以下のような式が成り立ちます。
(c)の場合の弾性力
ばねの変位と弾性力の向きとの関係
図の(b),(c)を見ると分かるように、ばねの変位に対して、弾性力の向きは逆向きになっています。
変位の向きと弾性力の向きの関係
- ばねが縮んだとき:変位は左向き(-),弾性力は右向き(+)
- ばねが伸びたとき:変位は右向き(+) ,弾性力は左向き(-)
このことに気付くと、(b),(c)の両方を満たす式がどのようになるのかが分かってきます。
ばねが伸びたときと縮んだときの両方を満たす式
(*)式であれば、ばねの変位が正の場合でも負の場合でも、ベクトル量としての弾性力を求めることができます。
先ほども述べましたが、ばねの弾性力は、自然長から伸びると縮もうとする向きに働き、また、縮むと伸びようとする向きに働きます。このことを式に反映させたのがマイナスの符号です。
つまり、フックの法則の右辺にあるマイナスの符号は、自然長からの変位の向きと弾性力の向きとが常に逆向きであることを表しています。ですから、実際の物理現象をきちんと反映した式だと言えます。
もし、「F(x)=kx」とした場合、弾性力の大きさを得ることはできますが、弾性力の向きの情報を得ることはできません。
高校物理では大きさだけでなく、向きも併せて考えます。そうなると、スカラー量としての等式「F(x)=kx」は正直なところ使い勝手が良くありません。
それに対して、 ベクトル量としての等式「F(x)=-kx」は、向きと大きさをもつベクトル量を正しく反映してくれるので、とても使い勝手が良い式です。
「F(x)=-kx」の式を使いこなして、向きと大きさの情報を一度で得られるようにしておきましょう。
スカラー量としての等式とベクトル量としての等式
- $F(x)=kx$:スカラー量(大きさ)を扱った等式
- $F(x)=-kx$:ベクトル量(大きさ+向き)を扱った等式
ベクトル量を扱った等式で弾性力を求めよう。
さいごにもう一度

どうじゃ、分かったかの?

はいっ! 扱う数量がベクトル量かスカラー量かで式が違ったのですね。

その通りじゃ。

ベクトル量を扱うようになると、マイナスの符号ありの式を使わないと面倒だということも分かりました。

ちなみに、$F(x)=-kx$ はベクトル量を扱うことから、弾性力や変位を $\vec{ F } \ , \ \vec{ x }$ と表記する場合もあるんじゃ。

矢印が付いていますねっ! ベクトル量ってすぐに分かりますっ!

あとは公式そのものを覚えるのは大切じゃが、文字の定義も併せて覚えてほしいのぅ。

そうですね。文字の定義には注意が向いていませんでした。

極端な話、文字は何でも良いわけじゃ。だから、どんな数量を扱っているのかを覚えることが大切なんじゃ。

仰る通りです。これからは注意深く公式を覚えますっ!

めげないところがメガネ君の良いところじゃ。次回も楽しみにしとるよ。
物理・物理基礎のオススメ本
- 宇宙一わかりやすい高校物理(力学・波動)
- 宇宙一わかりやすい高校物理(電磁気・熱・原子)
物理入門者や、物理を苦手にしている人に導入書としておすすめです。教科書が学習の中心であるべきですが、どうしても教科書で理解できない箇所が出てきたら本書で補完すると良いでしょう。イラストが豊富なので独学でも使えます。
分冊になっているので、力学と波動以外の分野はもう1冊の方になります。
- 秘伝の物理講義[力学・波動]
- 秘伝の物理講義[電磁気・熱・原子]
YouTubeで完全公開されている講義を再現したのが本冊です。また、別冊の「動画テキスト兼ポイント集」で物理の「わからない」を解決できます。公開模試、学校平均点全国No.1を取らせた実力派教師の講義は一読の価値あり。独学にも向き、標準以上も対応可能です。
分冊になっているので、力学と波動以外の分野はもう1冊の方になります。
物理教室(河合塾series)
所有していますが、これ1冊で基礎から応用まで十分対応できます。理系志望者は一読してほしいのが本書です。
物理の内容が分野ごとに章立てされており、各分野ごとに筋道を通した理解ができます。網羅性が高いのは当然ですが、「物理的な見方や考え方」が自然に身につくように丁寧に解説されています。
また、入試を意識して問題を多く扱っているのも特徴で、問題集代わりにも使えます。基礎を身に着けたい人は参考書として、応用力を養いたい人は問題集として、実力に応じて使いこなせる構成になっています。
問題集の『物理のエッセンス』は有名ですが、同じ河合塾seriesなので相性も良いです。
















