図形の性質|正三角形の外心、内心、重心について

今回は正三角形の重心、外心、内心について学習しましょう。外心、内心、重心は既に学習しましたが、ここではこれらが正三角形ではどんな関係にあるかを学習します。
図形の性質の単元全般に言えますが、この辺りから性質に関する証明問題が増えてきます。証明問題を苦手とする人は多いですが、取り組む価値はあります。
証明問題ではこれまでに学習したことをいかに使いこなすかを学べるので、より深く理解するのに非常に役立ちます。また、論理的な思考力を身に付けることもできるので、積極的に証明問題に取り組みましょう。
記事の画像が見辛いときはクリックすると拡大できます。
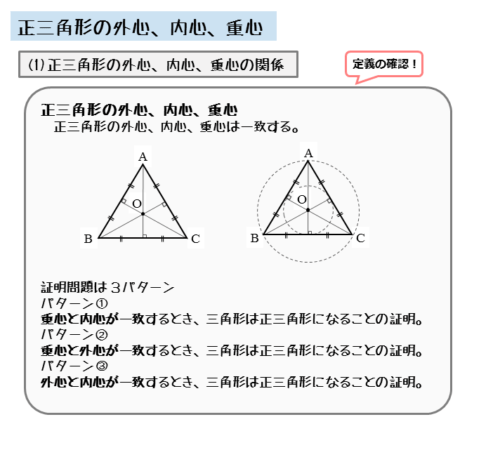
正三角形の外心、内心、重心の関係
一般に、三角形の外心、内心、重心は一致しません。しかし、正三角形であれば、外心、内心、重心の3つは一致します。
一見すると一致するかどうかが不明なので、たとえば「三角形の外心や内心が一致するとき、正三角形となっていることを証明せよ」などの問題がよく出題されます。主に3つのパターンがあります。
証明問題のパターン
- 三角形の重心と内心が一致するとき、正三角形であることを証明する
- 三角形の重心と外心が一致するとき、正三角形であることを証明する
- 三角形の外心と内心が一致するとき、正三角形であることを証明する
外心、内心、重心の性質を覚えるのはもちろんですが、性質をどのように証明に利用するのかを知らなければなりません。どのパターンでもきちんと証明できるようにしておきましょう。もちろん既習内容の復習にもなります。
三角形の重心と内心が一致するとき
1番目のパターンを証明してみましょう。
証明問題パターン1
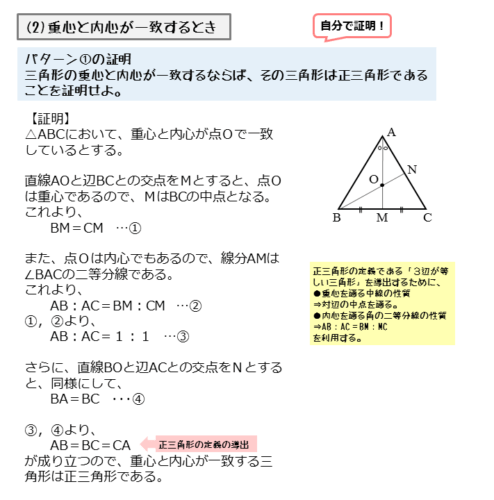
三角形の重心と内心が一致するならば、その三角形は正三角形である。
重心と内心の性質を確認しながら証明に取り組むと良いでしょう。
正三角形であることの証明は、正三角形の定義から3辺が等しいことを示します。3辺が等しいことを重心や内心の性質を利用して示します。
なお、辺が等しいことを示す方法は他にもあります。よく使われる方法としては、たとえば、合同であることや二等辺三角形であることを示す方法があります。
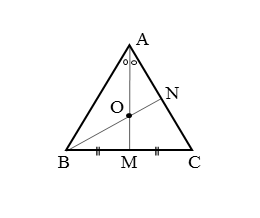
△ABCにおいて、重心と内心が一致する点をO、直線AOと辺BCとの交点をM、直線BOと辺CAとの交点をNとします。
線分AMに注目しましょう。
点Oは重心かつ内心なので、線分AMは中線かつ∠BACの二等分線です。このことから、以下のような関係が得られます。
パターン1の証明
点 $M$ は中点なので
\begin{align*} \quad BM = CM \end{align*}よって
\begin{align*} \quad BM : CM = 1:1 \quad \cdots \text{①} \end{align*}また、角の二等分線の性質より
\begin{align*} \quad AB : CA = BM : CM \end{align*}①より
\begin{align*} \quad AB : CA = 1 : 1 \end{align*}したがって
\begin{align*} \quad AB = CA \end{align*}これで2辺が等しいことを示すことができました。線分BNについても同じように考えると、AB=BCを示すことができます。この2つの結果からAB=BC=CAを示すことができます。
以上のことから、△ABCは3辺が等しい三角形、すなわち正三角形です。したがって、三角形の重心と内心が一致するならば、その三角形は正三角形であると言えます。
これまでをまとめると以下のようになります。
重心と内心が一致するパターンでは、中線と角の二等分線の性質から三角形の2辺が等しいことを示す。
三角形の重心と外心が一致するとき
2番目のパターンを証明してみましょう。
証明問題パターン2
三角形の重心と外心が一致するならば、その三角形は正三角形である。
3辺が等しいことを示すために、重心や外心の性質を利用します。
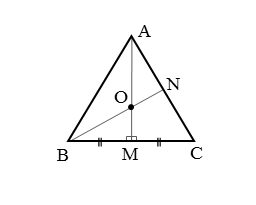
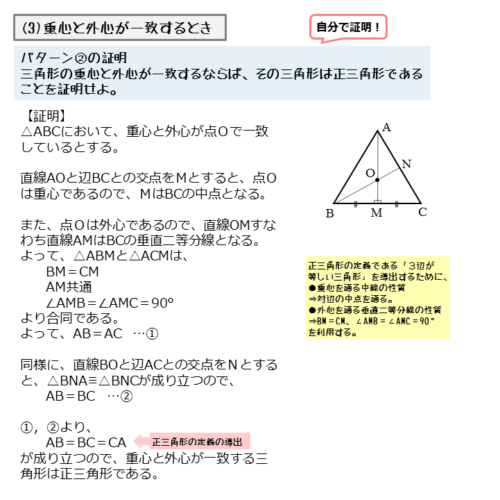
△ABCにおいて、重心と外心が一致する点をO、直線AOと辺BCとの交点をM、直線BOと辺CAとの交点をNとします。
線分AMに注目しましょう。
点Oは重心かつ外心なので、線分AMは中線かつ線分BCの垂直二等分線です。このことから、△ABMと△ACMについて以下のような関係が得られます。
パターン2の証明
点 $M$ は中点なので
\begin{align*} \quad BM = CM \end{align*}また、垂直二等分線の性質より
\begin{align*} \quad \angle AMB = \angle AMC = 90^{\circ} \end{align*}さらに、線分 $AM$ は共通。
よって
\begin{align*} \quad \triangle ABM \equiv \triangle ACM \end{align*}したがって
\begin{align*} \quad AB = CA \end{align*}これで2辺が等しいことを示すことができました。線分BNについても同じように考えると、AB=BCを示すことができます。この2つの結果からAB=BC=CAを示すことができます。
以上のことから、△ABCは3辺が等しい三角形、すなわち正三角形です。したがって、三角形の重心と外心が一致するならば、その三角形は正三角形であると言えます。
これまでをまとめると以下のようになります。
重心と外心が一致するパターンでは、中線と辺の垂直二等分線の性質から合同証明し、三角形の2辺が等しいことを示す。
三角形の外心と内心が一致するとき
3番目のパターンを証明してみましょう。
証明問題パターン3
三角形の外心と内心が一致するならば、その三角形は正三角形である。
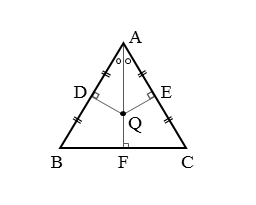
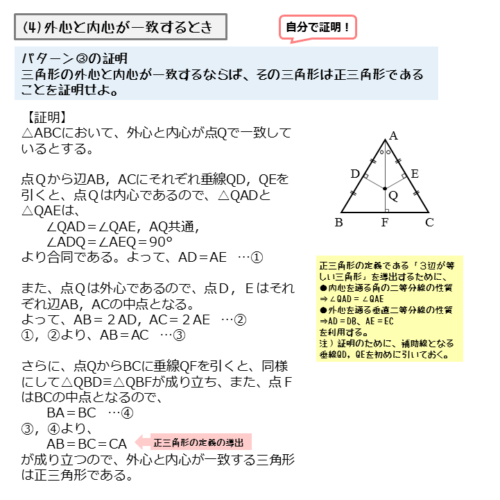
△ABCにおいて、外心と内心が一致する点をQ、点Qから辺AB,ACに下ろした垂線の足をそれぞれD,E、直線AQと辺BCとの交点をFとします。
線分AFに注目しましょう。
点Qは外心かつ内心なので、線分AFは辺BCの垂直二等分線かつ∠BACの二等分線です。
これが分かればこれまでと同じ要領で証明できますが、ここでは少し違ったアプローチで証明します。△QADと△QAEにについて以下のような関係が得られます。
パターン3の証明 1⃣
$QD \ , \ QE$ は垂線なので
\begin{align*} \quad \angle ADQ = \angle AEQ = 90^{\circ} \end{align*}よって、$\triangle QAD \ , \ \triangle QAE$ は直角三角形。
また、$AF$ は $\angle BAC$ の二等分線なので
\begin{align*} \quad \angle BAQ = \angle CAQ \end{align*}さらに、$AQ$ は共通。
よって
\begin{align*} \quad \triangle QAD \equiv \triangle QAE \end{align*}したがって
\begin{align*} \quad AD = AE \end{align*}ここで注意したいのは、△QADと△QAEの合同証明でAB=ACを導出しているわけではないことです。
内心の性質から言えることが、 辺AB,ACの関係ではなく、辺AB,ACの一部である線分AD,AEの関係だからです。ですから、まだ続きがあります。
パターン3の証明 2⃣
外心 $Q$ を通る直線 $QD \ , \ QE$ は垂直二等分線であるので
\begin{align*} \quad AB = 2AD \ , \ AC = 2AE \end{align*}ここで $AD = AE$ より
\begin{align*} \quad AB = AC \end{align*}これでやっと△ABCの2辺が等しいことを示すことができました。
これと同じように考えると、△QBDと△QBFについても合同証明から、BD=BFを示すことができます。また、垂直二等分線の性質からAB=BCも示すことができます。
以上のことから、AB=BC=ACを示すことができるので、△ABCは3辺が等しい三角形、すなわち正三角形になります。
したがって、三角形の外心と内心が一致するならば、その三角形は正三角形であると言えます。
これまでをまとめると以下のようになります。
重心と外心が一致するパターンでは、直角三角形を自分で作って合同証明し、辺の垂直二等分線の性質から三角形の2辺が等しいことを示す。
それぞれのパターンごとに結論までの流れが若干異なりますが、最終目標はどれもAB=BC=CAを示すことです。
なお、外心と内心のパターン3では他のパターンよりも手を加える必要がありますが、他のアプローチ(たとえばパターン1,2)でも証明できます。
自分なりに考えてみると良い訓練になるでしょう。その際には因果関係(AなのでB)をしっかり示すことを心掛けましょう。
証明問題は難しいイメージがありますが、演習をこなしていくときちんとコツを掴めます。覚えた知識の使い方や論法を知ることができるので、積極的に取り組みましょう。
Recommended books
オススメその1
予習の際に理解が進めば授業のスピードについていくことができ、復習や課題をこなす時間も少なくて済みます。予習や復習の補助教材に向いている教材が『とってもやさしい数学』シリーズです。
とってもやさしい数学1・Aでは2冊とも中学の履修内容にも触れており、中学と高校の学習内容のつながりを把握しやすい教材です。
基礎的な内容を扱っているので、数学が苦手な人でも取り組みやすくなっています。興味のある人はぜひ一読してみて下さい。
『高校とってもやさしい数学1・A 改訂版 その1』は「数と式」「2次関数」の単元を扱っています。
『高校とってもやさしい数学1・A 改訂版 その2』は「場合の数」「確率」「整数の性質」「図形の性質」「三角比」の単元を扱っています。
予習や復習などの日常学習に使いやすいのでおすすめです。
オススメその2
高校では記述する力がないと問題を解くのも一苦労です。一足飛びに答えが出てくるような問題が少ないので、過程を書き残していく必要があるからです。
そうは言っても答案の書き方に特化した教材はなかなか見当たらないので、模範解答を参考にしながら記述の仕方を身に付けていくのが一般的ではないかと思います。
ここで紹介する『総合的研究 記述式答案の書き方ーー数学I・A・II・B』は、答案の書き方を身に付けることができる教材です。数学の答案では一般的に因果関係を示しながら記述していきます。これは模範解答を読めば明らかです。
学習の際に「書く」ことを疎かにしなければ、因果関係を意識しながら学習する習慣が徐々に身に付いていきます。因果関係を理解できることは、教科書や参考書を読むときはもちろん、試験では読解問題などに大いに役立ちます。
このように記述する能力は高校の学習において意外と大切な能力ですが、時間を掛けて身に付けていくものです。ですから、やみくもにやっていては時間の浪費になってしまいます。
その助けになるのが『総合的研究 記述式答案の書き方ーー数学I・A・II・B』ではないかと思います。他とはちょっと違ったアプローチで作成されているので、手を出しにくいかもしれませんが、個人的にはおすすめの教材です。
『総合的研究 数学I・A記述式答案の書き方問題集』というものもあります。
さいごに、もう一度、頭の中を整理しよう
- 正三角形の外心、内心、重心は一致する。
- 外心、内心、重心の組合せに応じた証明パターンがある。
- 重心と内心が一致するパターンでは、中線や角の二等分線の性質を利用。
- 重心と外心が一致するパターンでは、中線や垂直二等分線の性質を利用。
- 外心と内心が一致するパターンでは、自分で直角三角形を作り、角の二等分線と垂直二等分線の性質を利用。