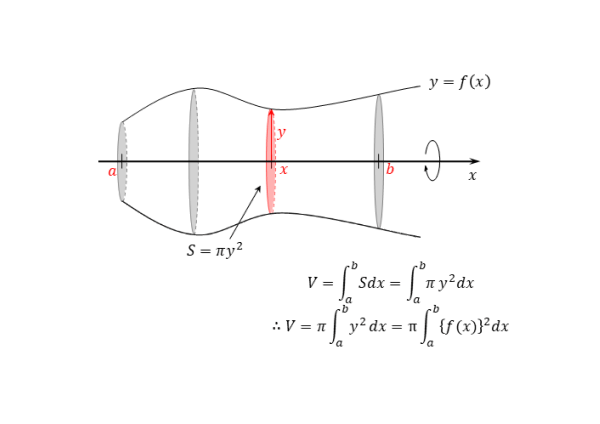数学3|回転体を扱った入試問題を解いてみよう

今回、紹介する問題も図形問題の一種ですが、回転体の体積問題です。回転軸がx軸とy軸のどちらであっても、考え方に違いはありません。
図がないと間違いやすいので、きちんと作図して考えましょう。
過去問を解いてみよう
過去の入試問題になります。最初は力試しに自力で解いてみることをお勧めします。
問題
図形 $C: \ y^{2}+(x-1)^{2} \leqq 4$ を $y$ 軸まわりに回転させてできる立体の体積を求めよ。
自力で解けない人は、以下の「問題を解く前に」を確認しましょう。
問題を解く前に
方針を決めよう
マーク形式レベルであれば、方針が複数あることはほとんどないので、問題を読めばすぐに取り掛かれます。
それに対して、記述形式レベル(2次試験レベル)になると、方針の候補が1つではない問題が多くなります。ですから、できるだけ効率良く解ける方針を採用しなければなりません。
つまり、記述形式レベルの問題を解くには、記述する前に方針をきちんと決めることがとても大切になります。
図形問題であれば、図を見ながら方針を考えていくことになります。
回転体の体積は断面を重ね合わせる
回転体の体積を求めるときに注意すべきことがあります。
問題では「グラフや軸に囲まれた部分を回転させて回転体を作った」とありますが、平面図形を回転させて体積を求めてはいけません。積分ではこのようなやり方で体積を求めることはできません。
正しくは「回転軸に垂直な断面を重ね合わせて体積を求める」です。面積でも細かな短冊の面積を足し合わせて面積を求めます。区分求積法をイメージすると分かりやすいかもしれません。
これと同じように、回転軸に垂直な断面の面積を足し合わせることによって、回転体の体積を求めます。
x軸回りの回転体の場合は以下の通りです。グラフとx軸に挟まれた部分の図形を回転させています。回転軸はx軸です。
x軸に対して垂直に回転体を切った断面の面積を、回転体の高さの範囲(aからbまで)で足し合わせます。断面は円となりますが、円の半径はグラフ上の点のy座標です。
x軸まわりの回転体の体積
$y=f(x) \ , \ x=a \ , \ x=b$ のグラフと $x$ 軸に囲まれた部分を $x$ 軸まわりに回転させたときの回転体の体積 $V$ とする。
また、回転軸に垂直で、$y=f(x)$ 上の任意の点 $(x \ , \ y)$ を通る断面の面積を $S$ とする。
このとき、回転体の体積 $V$ は
\begin{align*} \quad V=\int_a^b S dx \end{align*}ここで
\begin{align*} \quad S=\pi y^{2} \end{align*}であるので
\begin{align*} \quad V=\int_a^b {\pi y^{2}} dx \end{align*}よって
\begin{align*} \quad V=\pi \int_a^b {y^{2}} dx \end{align*}さらに、$y=f(x)$ より
\begin{align*} \quad V=\pi \int_a^b {\left\{f(x)^{2} \right\}} dx \end{align*}無数に切った断面の面積を足し合わせる作業を、aからbまでの定積分で行うことができます。
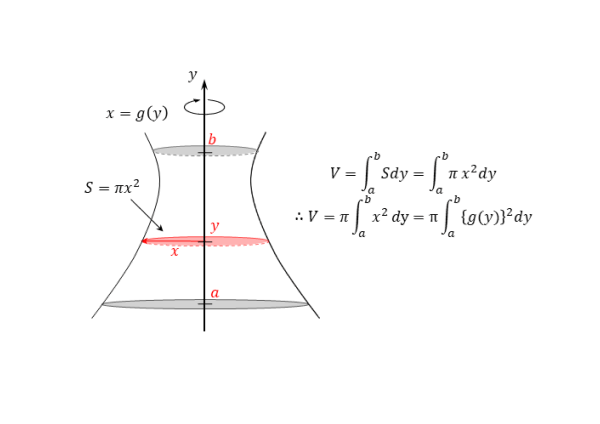
y軸回りの回転体の場合は以下の通りです。グラフとy軸に挟まれた部分の図形を回転させています。回転軸はy軸です。
y軸に対して垂直に回転体を切った断面の面積を、回転体の高さの範囲(aからbまで)で足し合わせます。断面の円の半径は、グラフ上の点のx座標です。
y軸まわりの回転体の体積
$y=f(x) \ , \ y=a \ , \ y=b$ のグラフと $y$ 軸に囲まれた部分を $y$ 軸まわりに回転させたときの回転体の体積 $V$ とする。
また、回転軸に垂直で、$x=g(y)$ 上の任意の点 $(x \ , \ y)$ を通る断面の面積を $S$ とする。ここで、$x=g(y)$ は $y=f(x)$ を $x$ について変形したものである。
このとき、回転体の体積 $V$ は
\begin{align*} \quad V=\int_a^b S dy \end{align*}ここで
\begin{align*} \quad S=\pi x^{2} \end{align*}であるので
\begin{align*} \quad V=\int_a^b {\pi x^{2}} dy \end{align*}よって
\begin{align*} \quad V=\pi \int_a^b {x^{2}} dy \end{align*}さらに、$x=g(y)$ より
\begin{align*} \quad V=\pi \int_a^b {\left\{g(y)^{2} \right\}} dy \end{align*}回転軸によって変数が異なるので注意しましょう。回転軸がx軸であれば、変数はxなので、積分範囲はx座標の取り得る範囲です。
また、回転軸がy軸であれば、変数はyなので、積分範囲はy座標の取り得る範囲です。
回転軸の両側に平面図形がある場合
平面図形を回転させる場合、回転軸が平面図形を通って左右、または上下に分割することがあります。
このような場合、両側の平面図形をそれぞれ回転させて、重なる部分と重ならない部分を把握することが大切です。
重なる部分であれば、大きい方の平面図形に含まれるので無視できます。しかし、重ならない部分であれば、その部分が影響するので考慮しなければなりません。
また、回転軸によって平面図形が分割される場合、たいてい余分な部分が出てくるので、それを除く処理が必要になります。
問題の解答・解説
問題
図形 $C: \ y^{2}+(x-1)^{2} \leqq 4$ を $y$ 軸まわりに回転させてできる立体の体積を求めよ。
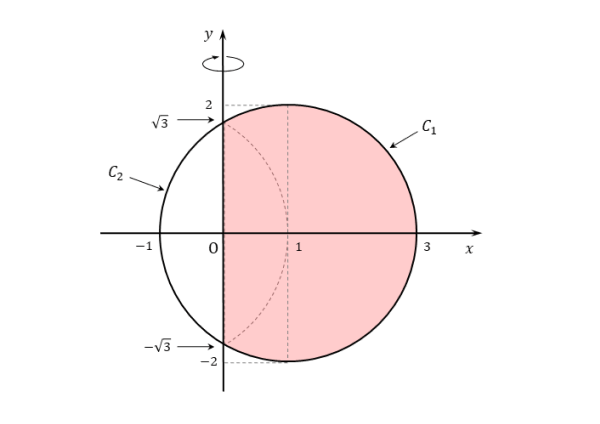
問題で与えられた関数のグラフを図示すると以下の通りです。
与えられた式は不等式なので、不等式の表す領域は、円の周内部と周上、つまり円板となります。
図では、回転体に影響する部分だけに色付けしてあるので勘違いしないようにしましょう。
回転軸はy軸です。回転させる平面図形は円板です。円板はy軸によって2つに分割されています。
また、y軸に平行、かつ円の中心を通る直線x=1によって円周を切ったとき、円周の右側部分をC1、左側部分をC2としています。
y軸に対して、円の左側部分(C2のうちy軸よりも左側部分)と右側部分(C1とC2のうちy軸よりも右側部分)をそれぞれ回転させてみましょう。
左側部分は右側部分に含まれるので、右側部分だけで考えれば良いことが分かります。また、円板はx軸に関して対称な図形になっていることも大切です。
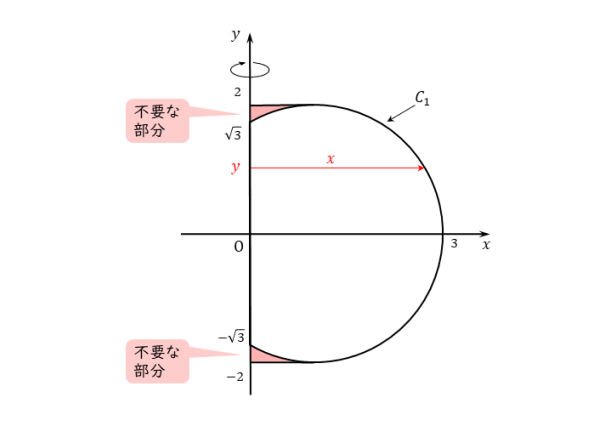
C1がC2を含むことから、C1の式だけで定積分すれば良さそうに感じます。ここで気付かなければならないのは、C1の式だけで定積分すると余分な部分を含んでしまうということです。
余分な部分は、周C2の一部とy軸に挟まれた図形(図の色付き部分)を回転させてできる回転体に相当します。このことを考慮して立式しましょう。
解答例は以下のようになります。まずは体積を求める式を立式します。
問題の解答例 1⃣
円板
\begin{align*} \quad C: \ y^{2}+(x-1)^{2} \leqq 4 \end{align*}の周の方程式は
\begin{align*} \quad y^{2}+(x-1)^{2} = 4 \end{align*}より
\begin{align*} \quad x=1 \pm \sqrt{4-y^{2}} \end{align*}ここで
\begin{align*} &\quad C_{1} : \ x=1 + \sqrt{4-y^{2}} \quad \left( 1 \leqq x \leqq 3 \right) \\[ 7pt ] &\quad C_{2} : \ x=1 – \sqrt{4-y^{2}} \quad \left( -1 \leqq x \leqq 1 \right) \end{align*}とおく。
$C_{2}$ のうち $y$ 軸の左側にある部分を $y$ 軸に関して対称移動すると、$C_{1}$ と $y$ 軸に挟まれる領域に含まれる。
よって、円板 $C$ を $y$ 軸まわりに $1$ 回転させてできる立体の体積 $V$ は $x$ 軸に関する対称性も考慮すると
\begin{align*} \quad V=2 \left\{ \pi \int_0^2 \left(1 + \sqrt{4-y^{2}} \right)^{2} dy-\pi \int_{\sqrt{3}}^2 \left(1 – \sqrt{4-y^{2}} \right)^{2} dy \right\} \end{align*}あとは丁寧に計算していきます。計算を工夫することも忘れないようにしましょう。
問題の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad V=2 \left\{ \pi \int_0^2 \left(1 + \sqrt{4-y^{2}} \right)^{2} dy -\pi \int_{\sqrt{3}}^2 \left(1 – \sqrt{4-y^{2}} \right)^{2} dy \right\} \end{align*}整理すると
\begin{align*} &\quad V=2 \pi \left[ \int_0^2 \left\{\left(5-y^{2} \right)+2\sqrt{4-y^{2}} \right\} dy -\int_{\sqrt{3}}^2 \left\{\left(5-y^{2} \right)-2\sqrt{4-y^{2}} \right\} dy \right] \\[ 7pt ] &\quad =2 \pi \left\{ \int_0^2 \left(5-y^{2} \right) dy-\int_{\sqrt{3}}^2 \left(5-y^{2} \right) dy +\int_0^2 2\sqrt{4-y^{2}} dy +\int_{\sqrt{3}}^2 2\sqrt{4-y^{2}} dy \right\} \end{align*}ここで
\begin{align*} &\quad \int_0^2 \left(5-y^{2} \right) dy-\int_{\sqrt{3}}^2 \left(5-y^{2} \right) dy =\int_0^{\sqrt{3}} \left(5-y^{2} \right) dy \\[ 7pt ] &\quad \int_0^2 2\sqrt{4-y^{2}} dy +\int_{\sqrt{3}}^2 2\sqrt{4-y^{2}} dy =2\int_0^2 2\sqrt{4-y^{2}} dy -\int_0^{\sqrt{3}} 2\sqrt{4-y^{2}} dy \end{align*}であることを利用して
\begin{align*} \quad V=2 \pi \left\{ \int_0^{\sqrt{3}} \left(5-y^{2} \right) dy+4\int_0^2 \sqrt{4-y^{2}} dy -2\int_0^{\sqrt{3}} \sqrt{4-y^{2}} dy \right\} \quad \cdots \text{①} \end{align*}①式の導出では、定積分の性質を利用しています。もう少し丁寧に計算過程を記述すると以下の通りです。
定積分の性質を上手に利用しよう
積分範囲に注意して
\begin{align*} &\underline{\int_0^2 \left(5-y^{2} \right) dy}-\int_{\sqrt{3}}^2 \left(5-y^{2} \right) dy \\[ 7pt ] &\underline{\int_0^{\sqrt{3}} \left(5-y^{2} \right) dy+\int_{\sqrt{3}}^2 \left(5-y^{2} \right) dy}-\int_{\sqrt{3}}^2 \left(5-y^{2} \right) dy \\[ 7pt ] = &\int_0^{\sqrt{3}} \left(5-y^{2} \right) dy \end{align*}同様にして
\begin{align*} &\int_0^2 2\sqrt{4-y^{2}} dy +\underline{\int_{\sqrt{3}}^2 2\sqrt{4-y^{2}} dy} \\[ 7pt ] = &\int_0^2 2\sqrt{4-y^{2}} dy +\underline{\int_0^2 2\sqrt{4-y^{2}} dy-\int_0^{\sqrt{3}} 2\sqrt{4-y^{2}} dy} \\[ 7pt ] = &2\int_0^2 2\sqrt{4-y^{2}} dy-\int_0^{\sqrt{3}} 2\sqrt{4-y^{2}} dy \\[ 7pt ] = &4\int_0^2 \sqrt{4-y^{2}} dy-2\int_0^{\sqrt{3}} \sqrt{4-y^{2}} dy \end{align*}①式の中には3つの定積分があります。計算過程が煩雑になるので、このまま計算するのではなく、それぞれを抜き出して計算します。
1つ目の定積分は素直に計算します。
問題の解答例 3⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad =2 \pi \left\{ \int_0^{\sqrt{3}} \left(5-y^{2} \right) dy+4\int_0^2 \sqrt{4-y^{2}} dy -2\int_0^{\sqrt{3}} \sqrt{4-y^{2}} dy \right\} \quad \cdots \text{①} \end{align*}ここで
\begin{align*} \quad \int_0^{\sqrt{3}} \left(5-y^{2} \right) dy=\left[ 5y-\frac{1}{3}y^{3} \right]_0^{\sqrt{3}}=4\sqrt{3} \end{align*}残りの2つは工夫すると簡単に計算できます。
問題の解答例 4⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \int_0^{\sqrt{3}} \left(5-y^{2} \right) dy=\left[ 5y-\frac{1}{3}y^{3} \right]_0^{\sqrt{3}}=4 \sqrt{3} \end{align*}また
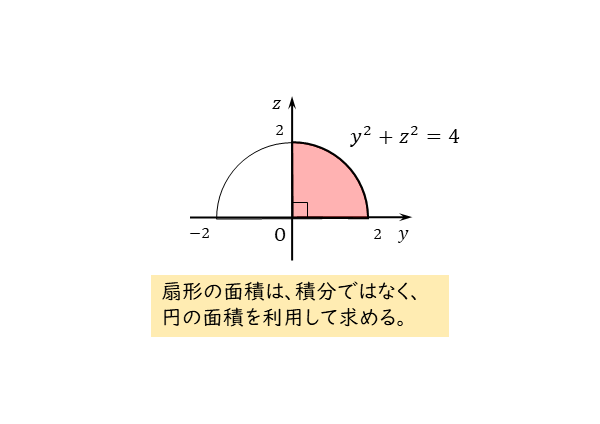
\begin{align*} \quad \int_0^2 \sqrt{4-y^{2}} dy \end{align*}は四分円の面積であるので
\begin{align*} \quad \pi \cdot 2^{2} \cdot \frac{1}{4}=\pi \end{align*}定積分が円の面積に相当することが分かっていれば、わざわざ定積分の計算をする必要はありません。よく利用するので覚えておくと良いでしょう。
円の面積に置換できる定積分
\begin{align*} \quad \int_0^{a} \sqrt{a^{2}-x^{2}} dx=\frac{1}{4} \pi a^{2} \end{align*}定積分の式において
\begin{align*} \quad y=\sqrt{a^{2}-x^{2}} \end{align*}とおくと
\begin{align*} \quad x^{2}+y^{2}=a^{2} \end{align*}ただし
\begin{align*} \quad 0 \leqq x \leqq a \end{align*}となるので、周の一部(第 $1$ 象限)を表す。
定積分は、この周の一部と $x$ 軸に挟まれる部分の面積となるので、四分円の面積に相当する。
3つ目も同様ですが、もう少し工夫が必要です。
問題の解答例 5⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \frac{\pi}{4} \cdot 2^{2}=\pi \end{align*}同様に
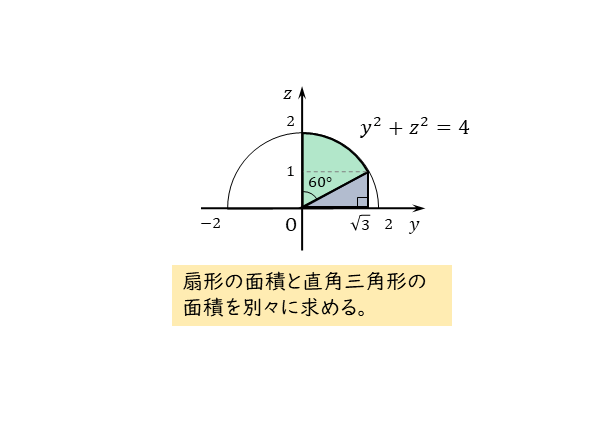
\begin{align*} \quad \int_0^{\sqrt{3}} \sqrt{ 4-y^{2} } dy \end{align*}は扇形と直角三角形の面積の和であるので
\begin{align*} \quad \pi \cdot 2^{2} \cdot \frac{1}{6}+\frac{1}{2} \cdot \sqrt{3} \cdot 1=\frac{2}{3} \pi+\frac{\sqrt{3}}{2} \end{align*}定積分の式のdyから、変数はyです。
変数yの積分範囲から、グラフとy軸に挟まれた部分(図の色付き部分)が求める面積です。
扇形と直角三角形に分割できるので、別々に面積を求めて足します。
もちろん、定積分をそのまま計算しても良いのですが、かなり面倒です。
さいごに①式に代入して、回転体の体積を求めます。定積分だけを足すのではなく、①式にきちんと代入しましょう。係数にも注意しましょう。
問題の解答例 6⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad =2 \pi \left\{ \int_0^{\sqrt{3}} \left(5-y^{2} \right) dy+4\int_0^2 \sqrt{4-y^{2}} dy -2\int_0^{\sqrt{3}} \sqrt{4-y^{2}} dy \right\} \quad \cdots \text{①} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad \int_0^{\sqrt{3}} \left(5-y^{2} \right) dy=\left[ 5y-\frac{1}{3}y^{3} \right]_0^{\sqrt{3}}=4 \sqrt{3} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad \pi \cdot 2^{2} \cdot \frac{1}{4}=\pi \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad \pi \cdot 2^{2} \cdot \frac{1}{6}+\frac{1}{2} \cdot \sqrt{3} \cdot 1=\frac{2}{3} \pi+\frac{\sqrt{3}}{2} \end{align*}これらを①に代入して
\begin{align*} \quad V=2 \pi \left\{ 4\sqrt{3}+4 \pi-2\left( \frac{2}{3} \pi+\frac{\sqrt{3}}{2} \right) \right\} \end{align*}整理すると
\begin{align*} \quad V=2 \pi \left( 3\sqrt{3}+\frac{8}{3} \pi \right) \end{align*}入試レベルの問題では、よく考えないとなかなか解けないものが多いです。そうなると、初見で完答するにはかなり難易度の高い問題です。
思考力が鍛えるためにも日頃から標準レベル以上の問題に積極的に取り組みたいところです。
共通テストでは「思考力・表現力・判断力」を試す問題が多く出題されることが分かっています。そのような問題に対応するためにも、覚えれば解けるような問題よりも、方針が必要な問題を多くこなすことが大切です。
Recommended books
メタ認知のためにも演習をこなすことは大切です。はじめのうちは何事も質よりも量の方を意識してこなす方が良いと思います。全体を一度通ってから質を考えると効率が良いでしょう。
特に、思考力を問われる問題の比重が過去に比べて増えてきています。パターンの暗記だけでは対応できなくなってきています。
オススメその1
そこで紹介するのが河合塾シリーズの『これからの大学入試に必要な数学の「思考力」を鍛える問題集』です。
河合塾数学科の考える「思考力・判断力・表現力」をまとめ、これに基づいて過去の入試問題を分析し、その中から思考力を養うために経験しておきたい問題を収集し解答・解説を収録。また、思考調査の問題を参考にして「共通テスト型問題」を作成。
センター試験から共通テストへと変わったことにより、「思考力・判断力・表現力」を問う問題が今まで以上に出題されると考えられます。これらは短期間で習得するのはなかなか難しいものです。日頃から訓練して身に付けるものなので、このような教材を利用してできるだけ早く取り組みたいところです。
オススメその2
バカロレア試験は、フランスの大学入学資格試験です。論述試験が中心です。思考力はもとより表現力も必要な試験です。
思考力・表現力を保障するには、大学教育の準備学力として、大学入試でどのような思考力・表現力を問うべきか。思考力・表現力を評価する論述型大学入試の実現に何が必要か。この思考力・表現力を中学校、高校でいかに育むべきか。本書では、論述試験中心のフランスの大学入学資格試験・バカロレア試験の問題や模範解答、採点規準、フランスの学校での授業観察などをもとに、これらの問いへのヒントを示す。第一人者が結集して執筆した、バカロレア研究の最前線。
海外に留学したいと考えている人にはおすすめです。思考力や表現力を短期間で養成するのは簡単ではありません。ですから、出来るだけ早く、意識的に取り組んでおいた方が良いでしょう。
オススメその3
高等学校の数学IIIの微分積分を、効率よく学ぶことができるように編まれた教科書。検定教科書の学習を前提とはせず、検定教科書に変わるものとして学ぶことを想定として記述。